最小生成树及其与最佳公共传输半径的关系

MST是通信网络中常用的拓扑结构象征性实例。在图G=（V，E）中，MST是该图的一个连通子集，它包含所有顶点，且能够实现边长总和最小化（或更为一般的权重）。一种用于构建这种结构的著名集中式算法是Kruskal算法，其主要工作原理如下：E的所有边按照权重升序排列，就会生成一个新的空集E′。对于排序后集合E中的每个边e来说，如果它在G′=（V′，E′）中不生成环路，则将它添加到E′中。由此形成的G′是G的一个MST。

图7-1给出了MST的一个实例，它是建立在随机UDG之上的。按照惯例，在无线网络中，边长可用作权重。需要注意的是，如果几条边具有相同的长度，则可能存在几个等价的MST，但这种不确定性可以轻易地被附加参数（如节点ID之间的比较）所打破。

关于MST的一个有趣的事实是，其最长边也与最佳公共传输半径相对应（即保持网络连通性所需的最小半径）。这可以直接根据Kruskal算法得出，该边是最后一个添加到E′中的边。

(www.xing528.com)

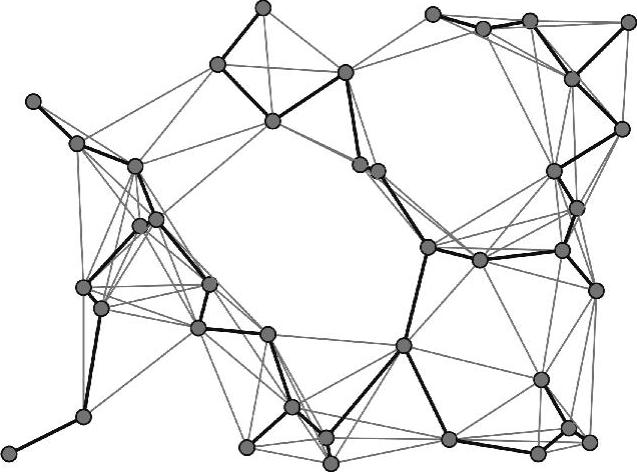
图7-1 随机单位图上的最小生成树

考虑到一些相关结果，参考文献（Penrose，1999）证明，网络中某个节点的“最远邻近”邻居和最长的MST边，趋于（当n→+∞时）同一个值。在临界值之前，连通概率在从0到1的区间内出现了一个非常尖锐的过渡（Bettstetter，2002）。另一个有趣的事实是所需的连接越少，可以节省的能量越多。参考文献（Santi and Blough，2003）举例说明，在二维和三维空间，将节点的关键传输范围减半，可以确保同一构件内的90%节点处于连通状态。

虽然构建一个MST和寻找最优传输范围问题密切相关，但它们都要用到诸如节点尺寸与密度或节点空间分布等全局知识。然后，该问题可以采用分布式模式来逼近最优值。下面，我们给出一些实现方法，这些方法都是基于局部MST的近似值。