微分算子的旋转不变性及构造二阶线性偏微分算子

对于图像中的边缘，一个简单的模型是：一条直线将两个相邻的区域分隔开来（如图10.1所示）。在对简单边缘模型的分析过程中，我们将会用到单位阶梯函数，其定义为：

注意：u(z)是对一维单位冲击函数δ的积分，即：

图10.1　理想的边缘是：区分两个具有相同亮度的图像区域的一条线。

假设：边缘所在的直线方程为

那么，对于简单的边缘模型，图像的亮度可以被写为如下形式：

其中，B1和B2分别为两个不同区域的亮度。图像亮度E(x,y)的（一阶）偏导数为：

这两个微分算子的结果依赖于边缘的朝向。向量

被称为图像亮度的梯度。当图像发生平移或旋转时，图像亮度的梯度（包括大小和方向）和图像之间的对应关系并不发生变化，从这个意义上说，图像亮度的梯度是一个和坐标系的选取无关的量。根据图像亮度的梯度，我们可以计算：图像中某一点(x,y)T和其附近任意一点(x1,y1)T之间的亮度变化率。这两个点确定了一个方向：

而点(x,y)T和(x1,y1)T之间的亮度变化率就是：亮度E(x,y)沿着方向n的方向导数，

当方向n选为图像亮度的梯度方向时，式(10.9)中的方向导数取得最大值，其大小

为梯度的模长。对于图10.1中的理想边缘，(www.xing528.com)

这个非线性算子是旋转对称的，因此，其检测结果与边缘的朝向无关。单位冲击函数δ的定义参见第6章相关内容。在实际应用中，我们常常直接使用来进行边缘检测。

进一步，对于某一个边缘点（也就是说，梯度的模长大于阈值），我们将图像亮度的梯度方向

定义为：边缘在该点处的法线方向。沿着这个方向，该点处的图像亮度变化最明显。边缘在该点处的切线方向垂直于法线方向，因此，该点处的切线方向为：

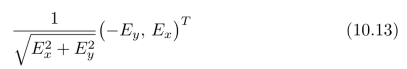
我们也将其称为：该点处的边缘方向。事实上，图像中的边缘比图10.1中的理想边缘复杂得多。在图10.2中，图像区域内部的亮度是渐变的，在边缘处，亮度并没有发生阶跃性突变，但是，亮度的变化发生了阶跃性突变。较之于图10.1中的理想边缘（也称为强边缘），我们将这类边缘称为弱边缘。

我们不能继续使用图像亮度的梯度（一阶导数）来对弱边缘进行检测，因为我们需要计算图像“亮度变化的变化”，这需要用到更高阶的微分或导数。我们可以尝试二阶导数，包括：

图10.2　弱边缘所分割出的区域内部的亮度并不是常数

上面三个二阶偏微分算子都不具有旋转不变性。在习题10.1中，我们将探索通过上面三个线性算子的线性组合：

来构造出一个满足旋转不变性的二阶线性偏微分算子。当且仅当a=c且b=0时，相应的二阶线性偏微分算子才满足旋转不变性，参见习题10.1。不是一般性，我们令a=c=1，可以得到图像E(x,y)的Lap lace算子处理结果：

注意：Laplace算子是满足旋转对称性的唯一的二阶线性偏微分算子。此外，二次变分：

也是旋转对称的，但是，它是一个二阶非线性算子。对于图10.2中的简单边缘模型，二次变分正好等于Lap lace算子处理结果的平方。

注意，对于上面提到的三种旋转对称算子，只有Lap lace算子的处理结果中保留了：边缘两侧亮度差的“正负”信息，即B2B1。这使得我们可以确定：在边缘增强图像中，边缘的哪一侧更亮。因此，Lap lace算子也是这三种算子中唯一的一个：有可能从边缘增强图像中复原出原始图像的算子。同时，在这三种旋转对称算子中，Lap lace算子也是唯一的线性算子！