使用不同范数规范化数据的方法优化

但是，我们可以找到一种方法，来设计出另外一种最小二乘法，从而使得我们可以：求得关于运动参数的解析解。我们求上面提到的积分公式(12.29)的最小值，而改为极小化如下表达式：

即：将被积函数乘以系数α2+β2。然后，我们用上面介绍的方法，对这个最小二乘问题进行求解。如果我们测得的光流没有受到噪声的影响，那么，这两个积分式都等于零，因此，这两个最优化问题的最优解是相同的。但是，如果我们所估计的光流并不精确，那么，最小化新的积分表达式(12.47)所得到的的结果，并不是针对L2范数的最佳拟合，而是针对另外一种称为Lαβ的范数形式，即：

即：将被积函数乘以系数α2+β2。然后，我们用上面介绍的方法，对这个最小二乘问题进行求解。如果我们测得的光流没有受到噪声的影响，那么，这两个积分式都等于零，因此，这两个最优化问题的最优解是相同的。但是，如果我们所估计的光流并不精确，那么，最小化新的积分表达式(12.47)所得到的的结果，并不是针对L2范数的最佳拟合，而是针对另外一种称为Lαβ的范数形式，即：

我们这里所求解的优化问题是：对各个点的误差赋予一个权重，光流越大的点，所赋予的权重也越大。如果光流的测量结果具有这样的特性：光流值越大，测量结果越精确，那么新的积分形式（即Lαβ范数）比原来的积分形式（即L2范数）更为合理。

使用哪种范数会得到最好的结果？这取决于：测量光流的过程中所产生的噪声的特性。第一种范数（即L2范数）形式更适合于：测量光流过程中所产生的噪声和光流的大小相互独立的情况。同时注意：如果我们真的想最小化L2范数，我们可以使用：最小化Lαβ范数所得的结果，作为初始值，然后，使用数值方法，对式(12.42)～(12.44)进行迭代求解。

现在，我们应用前面提到的求解最小二乘问题的方法，来最小化Lαβ范数情况下的积分式(12.47)。首先，我们求：被积函数关于Z的导数，然后，让求导结果等于零，从而得到最优的Z，即：

我们这里所求解的优化问题是：对各个点的误差赋予一个权重，光流越大的点，所赋予的权重也越大。如果光流的测量结果具有这样的特性：光流值越大，测量结果越精确，那么新的积分形式（即Lαβ范数）比原来的积分形式（即L2范数）更为合理。

使用哪种范数会得到最好的结果？这取决于：测量光流的过程中所产生的噪声的特性。第一种范数（即L2范数）形式更适合于：测量光流过程中所产生的噪声和光流的大小相互独立的情况。同时注意：如果我们真的想最小化L2范数，我们可以使用：最小化Lαβ范数所得的结果，作为初始值，然后，使用数值方法，对式(12.42)～(12.44)进行迭代求解。

现在，我们应用前面提到的求解最小二乘问题的方法，来最小化Lαβ范数情况下的积分式(12.47)。首先，我们求：被积函数关于Z的导数，然后，让求导结果等于零，从而得到最优的Z，即：

于是，我们得到：

于是，我们得到：

将上式带入公式(12.47)，最终，我们得到的优化目标函数为：

将上式带入公式(12.47)，最终，我们得到的优化目标函数为：

我们将积分表达式(12.51)记为g(U,V,W)。根据α和β的定义式(12.31)，我们可以将上式中的被积函数进一步写为：

我们将积分表达式(12.51)记为g(U,V,W)。根据α和β的定义式(12.31)，我们可以将上式中的被积函数进一步写为：

于是，我们可以将积分表达式(12.51)进一步整理为：

于是，我们可以将积分表达式(12.51)进一步整理为：

其中，

其中，

由于g(U,V,W)非负，并且当U=V=W=0时，g(U,V,W)=0。因此，我们找到了一个最优解：U=V=W=0。但是，这个最优解并不是我们所想要的！

事实上，为了得到由最小二乘模型（即：式(12.53)）确定的平移速度，我们必须求解式(12.53)中的g(U,V,W)取得极值的必要条件，也就是说，通过g(U,V,W)分别对U、V和W求偏导，然后，再令求导结果等于零，所得到的一组方程。最终，我们得到了下面的关于t=(U,V,W)T的齐次线性方程组[2]：

由于g(U,V,W)非负，并且当U=V=W=0时，g(U,V,W)=0。因此，我们找到了一个最优解：U=V=W=0。但是，这个最优解并不是我们所想要的！

事实上，为了得到由最小二乘模型（即：式(12.53)）确定的平移速度，我们必须求解式(12.53)中的g(U,V,W)取得极值的必要条件，也就是说，通过g(U,V,W)分别对U、V和W求偏导，然后，再令求导结果等于零，所得到的一组方程。最终，我们得到了下面的关于t=(U,V,W)T的齐次线性方程组[2]：

其中，

其中，

很明显，当且仅当G的行列式等于零时，式(12.60)才存在非零解。此时，式(12.60)中的三个方程线性相关，并且，非零解t可以相差一个常数因子。但是，通常情况下，由于数据中包含有噪声，因此，当t不等于零时，g(U,V,W)也不等于零。这使得：t=(0,0,0)T成为最优解。为了从另一方面来看出这一点，注意，式(12.53)中的g具有如下性质：

很明显，当且仅当G的行列式等于零时，式(12.60)才存在非零解。此时，式(12.60)中的三个方程线性相关，并且，非零解t可以相差一个常数因子。但是，通常情况下，由于数据中包含有噪声，因此，当t不等于零时，g(U,V,W)也不等于零。这使得：t=(0,0,0)T成为最优解。为了从另一方面来看出这一点，注意，式(12.53)中的g具有如下性质：

其中，k是一个常数。显然，当U=V=W=0时，g(U,V,W)取得最小值（由式(12.51)可知：g(U,V,W)≥0，由式(12.62)可知：g(0,0,0)=0，因此，g(0,0,0)≤g(U,V,W)）。

我们真正想要得到的是：对于固定长度的t，使得g最小的t的方向。因此，我们加入约束条件：t是一个单位向量。如果t为单位向量，那么，g的最小值等于：矩阵G的最小的特征值，并且，我们可以通过：与该特征值对应的特征向量，来确定：使得g取得最小值的t。我们注意到：g是一个二次型，并且，可以写为如下形式[2]：

其中，k是一个常数。显然，当U=V=W=0时，g(U,V,W)取得最小值（由式(12.51)可知：g(U,V,W)≥0，由式(12.62)可知：g(0,0,0)=0，因此，g(0,0,0)≤g(U,V,W)）。

我们真正想要得到的是：对于固定长度的t，使得g最小的t的方向。因此，我们加入约束条件：t是一个单位向量。如果t为单位向量，那么，g的最小值等于：矩阵G的最小的特征值，并且，我们可以通过：与该特征值对应的特征向量，来确定：使得g取得最小值的t。我们注意到：g是一个二次型，并且，可以写为如下形式[2]：

注意：由于a≥0，b≥0，c≥0，ab≥d2，bc≥e2，ca≥h2（后三个不等式可以通过Cauchy-Schw arz不等式得出），这说明G是一个半正定的实对称矩阵^[2]。因此，所有的特征值λi都是非负实数，这些特征值λi是下面的三阶多项式方程的解，即：三次方程的根是有解析表达式的。因此，我们可以得到：三次方程式(12.64)的最小正根的显式表达式。对于我们的问题，这给出了我们所需要的解。但是，为了内容的完整性，我们接下来会讨论：各种可能出现的病态情况。尽管这些情况在实际问题中很难碰到。(www.xing528.com)

注意：由于a≥0，b≥0，c≥0，ab≥d2，bc≥e2，ca≥h2（后三个不等式可以通过Cauchy-Schw arz不等式得出），这说明G是一个半正定的实对称矩阵^[2]。因此，所有的特征值λi都是非负实数，这些特征值λi是下面的三阶多项式方程的解，即：三次方程的根是有解析表达式的。因此，我们可以得到：三次方程式(12.64)的最小正根的显式表达式。对于我们的问题，这给出了我们所需要的解。但是，为了内容的完整性，我们接下来会讨论：各种可能出现的病态情况。尽管这些情况在实际问题中很难碰到。

注意，当且仅当G是奇异矩阵（也就是说，特征多项式(12.64)中的常数项等于零）时，才会出现λ=0的情况。事实上，如果G的行列式等于零，那么，我们可以找到一个平动速度t，使得g=0。从微积分的理论来说，这意味着光流“几乎处处”是正确的。也就是说，光流不一致的点的集合是一个零测集。因此，误差只可能出现在光流不连续的点上，而这些点正好是：（由函数Z所表示的）曲面上的不连续的地方（这些点也正好是：用已有的方法来计算光流时，产生很大误差的地方）。

注意，当且仅当G是奇异矩阵（也就是说，特征多项式(12.64)中的常数项等于零）时，才会出现λ=0的情况。事实上，如果G的行列式等于零，那么，我们可以找到一个平动速度t，使得g=0。从微积分的理论来说，这意味着光流“几乎处处”是正确的。也就是说，光流不一致的点的集合是一个零测集。因此，误差只可能出现在光流不连续的点上，而这些点正好是：（由函数Z所表示的）曲面上的不连续的地方（这些点也正好是：用已有的方法来计算光流时，产生很大误差的地方）。

在矩阵G的所有特征值中，不可能出现：有两个特征值为零的情况，因为，两个特征值为零意味着：在式(12.64)中的特征多项式中，常数项以及λ的一次项前面的系数都等于零，并且，λ2的项前面的系数不为零。这也意味着：ab=d2、bc=e2、ac=h2，并且，a、b、c不全为零。但是，由Cauchy-Schw arz不等式可知，上述三个等式意味着：u和v同时和xvyu成正比。只有当像平面上所有点(x,y)T的光流u=v=0时，才可能出现这种情况。但是此时，所有6个积分（即：式(12.54)～(12.59)）都等于零，这意味着三个特征值都等于零。这种情况没有太大的研究意义，因为这意味着光流处处为零，也就是说，相机的运动速度为零。

一旦知道了矩阵G的最小特征值，我们可以很容易求得：和给定数据匹配效果最好的平动速度。为了确定：和特征值λ1相对应的特征向量，我们需要求出下面的线性方程组的非零解，即：

在矩阵G的所有特征值中，不可能出现：有两个特征值为零的情况，因为，两个特征值为零意味着：在式(12.64)中的特征多项式中，常数项以及λ的一次项前面的系数都等于零，并且，λ2的项前面的系数不为零。这也意味着：ab=d2、bc=e2、ac=h2，并且，a、b、c不全为零。但是，由Cauchy-Schw arz不等式可知，上述三个等式意味着：u和v同时和xvyu成正比。只有当像平面上所有点(x,y)T的光流u=v=0时，才可能出现这种情况。但是此时，所有6个积分（即：式(12.54)～(12.59)）都等于零，这意味着三个特征值都等于零。这种情况没有太大的研究意义，因为这意味着光流处处为零，也就是说，相机的运动速度为零。

一旦知道了矩阵G的最小特征值，我们可以很容易求得：和给定数据匹配效果最好的平动速度。为了确定：和特征值λ1相对应的特征向量，我们需要求出下面的线性方程组的非零解，即：

由于λ1是特征值，因此，式(12.65)中的三个方程是线性相关的。我们暂时假设：矩阵G的三个特征值是各不相同的，也就是说，(GλI)的秩是2，其中I表示单位矩阵。于是，我们可以用：式(12.65)中的三个方程中的其中两个，来进行求解。其基本技巧是：将U和V表示成只含有W项的形式。

共有三种方法来实现这个过程。为了得到具有对称性的解，我们将用这三种方法求得的结果加在一起。于是，我们最终得到：

由于λ1是特征值，因此，式(12.65)中的三个方程是线性相关的。我们暂时假设：矩阵G的三个特征值是各不相同的，也就是说，(GλI)的秩是2，其中I表示单位矩阵。于是，我们可以用：式(12.65)中的三个方程中的其中两个，来进行求解。其基本技巧是：将U和V表示成只含有W项的形式。

共有三种方法来实现这个过程。为了得到具有对称性的解，我们将用这三种方法求得的结果加在一起。于是，我们最终得到：

注意，如果数据很好的话（即数据中包含较少的噪声），λ1将会很小。这种情况下，我们可以令：上式中的λ1=0，从而得到近似最优解（当然，此时我们没有必要再去求λ1的值）。我们可以对所求得的速度进行归一化，从而使得其大小等于1。我们还剩下一个难题：如果t是最优解，那么，t也将是最优解。但是，这两个“最优解”中只有一个使得Z取正值。我们可以通过：计算某些点的Z值，来确定t的正负。

注意，如果数据很好的话（即数据中包含较少的噪声），λ1将会很小。这种情况下，我们可以令：上式中的λ1=0，从而得到近似最优解（当然，此时我们没有必要再去求λ1的值）。我们可以对所求得的速度进行归一化，从而使得其大小等于1。我们还剩下一个难题：如果t是最优解，那么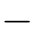，t也将是最优解。但是，这两个“最优解”中只有一个使得Z取正值。我们可以通过：计算某些点的Z值，来确定t的正负。

进一步，让我们来分析：矩阵G有两个相同的最小特征值的情况。我们可以找到一个简单的几何解释，来说明我们到目前为止所做的工作。考虑一个由g(U,V,W)=k所确定的曲面，其中k是一个常数。注意，我们总可以找到一个坐标系( U, V, W)，从而使得：在这个坐标系中，g(U,V,W)可以被写为：

进一步，让我们来分析：矩阵G有两个相同的最小特征值的情况。我们可以找到一个简单的几何解释，来说明我们到目前为止所做的工作。考虑一个由g(U,V,W)=k所确定的曲面，其中k是一个常数。注意，我们总可以找到一个坐标系(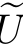 U, V, W)，从而使得：在这个坐标系中，g(U,V,W)可以被写为：

其中，λi（i=1,2,3）是二次型的三个特征值。如果这三个特征值都不为零，那么，g(U,V,W)=k是一个椭球，其三个相互垂直的对称轴的长度分别为：（其中，i=1,2,3）。我们所特别关心的是：常数k等于最小特征值的情况。此时，椭球的三个半轴的长度都小于或等于1。因此，这个椭球位于一个单位球里面。如果，较小的两个特征值的取值不同，那么，单位球有两个点和椭球相切。这两个点位于椭球的最长对称轴上。但是，如果较小的两个特征值相同，那么，单位球和椭球相切于：球面上的一个大圆。于是，所有位于：由这两个特征向量所张成的平面上的速度向量，具有相同的误差。最终，如果三个特征向量都相同，那么，并不存在“最好的”速度方向t，因为，此时椭球变成了一个单位球。

对于正好有一个特征值等于0的情况，也有一个简单的几何解释。此时，由g(U,V,W)=0所确定的曲面是一条直线。假设λ3=0，通过下面的方程：

其中，λi（i=1,2,3）是二次型的三个特征值。如果这三个特征值都不为零，那么，g(U,V,W)=k是一个椭球，其三个相互垂直的对称轴的长度分别为：（其中，i=1,2,3）。我们所特别关心的是：常数k等于最小特征值的情况。此时，椭球的三个半轴的长度都小于或等于1。因此，这个椭球位于一个单位球里面。如果，较小的两个特征值的取值不同，那么，单位球有两个点和椭球相切。这两个点位于椭球的最长对称轴上。但是，如果较小的两个特征值相同，那么，单位球和椭球相切于：球面上的一个大圆。于是，所有位于：由这两个特征向量所张成的平面上的速度向量，具有相同的误差。最终，如果三个特征向量都相同，那么，并不存在“最好的”速度方向t，因为，此时椭球变成了一个单位球。

对于正好有一个特征值等于0的情况，也有一个简单的几何解释。此时，由g(U,V,W)=0所确定的曲面是一条直线。假设λ3=0，通过下面的方程：

我们很容易看出这一点。注意：λ1和λ2都是正数。显然，单位球和这条线正好相交于两点，其中的一个点对应于Z取正数的情况。

我们刚刚讨论的方法是非常易于实现的。最终，我们需要将这个问题离散化，从而对其进行处理。我们可以推导出类似的方程，只是将“积分号”换成“求和符号”。于是，我们前面所提出的求解最小化问题的方法，可以用来对相应的离散情况进行求解。所求得的结果具有相似的形式，只是将“积分号”换成了“求和符号”。我们可以用：最大特征值和最小特征值的比值（即：条件数），来作为：对所得结果的可信度的一种衡量标准。如果条件数远大于1，那么，我们所求得的速度t（即：式(12.66)）对噪声的灵敏度很高。

当我们使用LZu v范数时，我们会得到：和前面讨论过的误差积分相同的形式。LZu,v范数的定义为：

我们很容易看出这一点。注意：λ1和λ2都是正数。显然，单位球和这条线正好相交于两点，其中的一个点对应于Z取正数的情况。

我们刚刚讨论的方法是非常易于实现的。最终，我们需要将这个问题离散化，从而对其进行处理。我们可以推导出类似的方程，只是将“积分号”换成“求和符号”。于是，我们前面所提出的求解最小化问题的方法，可以用来对相应的离散情况进行求解。所求得的结果具有相似的形式，只是将“积分号”换成了“求和符号”。我们可以用：最大特征值和最小特征值的比值（即：条件数），来作为：对所得结果的可信度的一种衡量标准。如果条件数远大于1，那么，我们所求得的速度t（即：式(12.66)）对噪声的灵敏度很高。

当我们使用LZu v范数时，我们会得到：和前面讨论过的误差积分相同的形式。LZu,v范数的定义为：

此外，我们可以让式(12.29)中的被积函数乘以Z2，而不是乘以α2+β2，从而，求得一个类似的解。对于这种情况，我们是针对：下面所定义的LZ范数，来求解最小化问题的。

LZ范数的定义为：

此外，我们可以让式(12.29)中的被积函数乘以Z2，而不是乘以α2+β2，从而，求得一个类似的解。对于这种情况，我们是针对：下面所定义的LZ范数，来求解最小化问题的。

LZ范数的定义为：

这里，场景中（距离相机）远的点所对应的光流，被赋予了更大的权重。对于：越大的光流对应于越低的精度的情况，最适合于使用这种范数形式。我们对这种情况进行求解，可以得到类似的g，但是，矩阵G中的六个参数a,b,c,d,e,f所对应的六个积分形式，会变得更加复杂。令人感到奇怪的是，这六个积分形式只依赖于：每一点的光流方向，而与光流的大小无关。我们也可以使用其他的约束条件，例如，令U2+V 2=1，或者W=1。

这里，场景中（距离相机）远的点所对应的光流，被赋予了更大的权重。对于：越大的光流对应于越低的精度的情况，最适合于使用这种范数形式。我们对这种情况进行求解，可以得到类似的g，但是，矩阵G中的六个参数a,b,c,d,e,f所对应的六个积分形式，会变得更加复杂。令人感到奇怪的是，这六个积分形式只依赖于：每一点的光流方向，而与光流的大小无关。我们也可以使用其他的约束条件，例如，令U2+V 2=1，或者W=1。