电路与电工技术：向量表示法的分析介绍

（1）复数简介

复数可表示成A=a+bi。其中a 为实部，b 为虚部，i=称为虚部单位。但由于在电路中i 通常表征电流强度，因此我们这里常用j 表示虚部单位，这样复数可表示成A=a+jb。

复数可以在复平面内用图形表示，也可以用不同形式的表达式表示。

1）复数的图形表示

①复数用点表示。

任意复数在复平面内均可找到其唯一对应的点。反之，复平面上的任意一点也均代表了一个唯一的复数。如图 3.2.2 可知，A1=1+j；A2=-3；A3=-3 -j2；A4=3 -j。

图3.2.2　复数用点表示

图3.2.3　复数用矢量表示

②复数用矢量表示。

任意复数在复平面内还可用其对应的矢量来表示，如图 3.2.3 所示。矢量的长度称为模，用 r 表示；矢量与实正半轴的夹角称为幅角，用θ 表示。模与幅角的大小决定了该复数的唯一性。

由图3.2.3 可知，复数用点表示法与用矢量表示法之间的换算关系为

2）复数的四种表达式

①代数式：

②三角函数式：

由式（3.2.3）可得

③指数式：

由数学中的欧拉公式ejθ=cos θ+j sin θ 得

④极坐标式：

在电路中，复数的模和幅角通常用更简明的方式表示

例3.2.1 写出1，-1，j，-j 的极坐标式，并在图3.2.4 复平面内作出其矢量图。

解 复数 1 的实部为 1，虚部为 0，其极坐标式为1=1∠0°；

复数-1 的实部为-1，虚部为0，其极坐标式为-1=1∠180°；

复数j 的实部为0，虚部为1，其极坐标式为j=1∠90°；

复数-j 的实部为0，虚部为-1，其极坐标式为-j=1∠-90°。

图3.2.4　矢量图

这就是四个复数的代数式和极坐标式的互换。

3）复数的四则运算

①加减运算。

设有两个复数分别为

故一般情况下，复数的加减运算应把复数写成代数式。也可用图解法，如图 3.2.5 所示。(www.xing528.com)

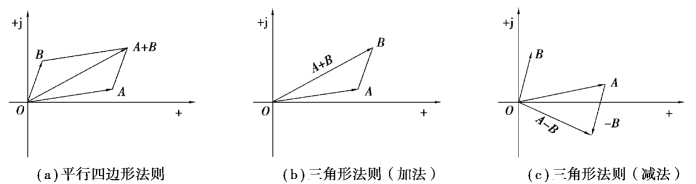
图3.2.5　平行四边形法则与三角形法则

例3.2.2 复数A1=5∠53°，A2=3，求 A1+A2 和A1 -A2，并在复平面内画出矢量图。

解 因为 A1=5∠53°=3+j4；A2=3

所以 A1+A2=（3+j4）+3=6+j4=6.3∠33.7°

画矢量图如图3.2.6 所示。

图3.2.6　矢量图

②乘除运算。

设有两个复数为A=r1 ∠θ1，B=r2 ∠θ2，则两个复数乘法运算

两个复数除法运算

故一般情况下，复数的乘除运算应把复数写成较为简便的极坐标式。

（2）正弦量的产生

1）旋转因子

通常把模为 1 的复数称为旋转因子，即ejθ=1 ∠θ。取任意复数A=r1ejθ=r1 ∠θ，

即任意复数乘以旋转因子后，其模不变，幅角在原来的基础上增加了θ，这就相当于把该复数逆时针旋转了θ 角，这一点从图3.2.7 中可以明显地看出。

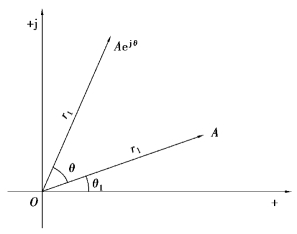
图3.2.7　旋转因子

2）正弦量的产生

前述分析中旋转因子1 ∠θ的幅角θ 为一常量，此时任意复数乘以该旋转因子后就会旋转θ 角。假使θ=ωt 是一个随时间匀速变化的角，其角速度为ω。不难想象，若任意复数乘以这个旋转因子1 ∠ωt 后，其复数矢量就会在原来的基础上逆时针旋转起来，且旋转的角速度也是ω。

如图3.2.8 所示，我们令某一复数为A=Um ∠ψu，那么有

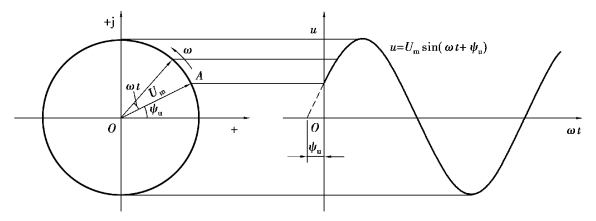
图3.2.8　正弦量的产生

（3）正弦量的相量表示法

正弦量有三种表示法：三角函数、波形图和相量（包括相量复数式和相量图）。其中，三角函数表达式和波形图我们在前面章节中已经用过，这里主要介绍正弦量的相量表示法。由式（3.2.3）可知，A 匀速旋转后可唯一对应一正弦量，即

例3.2.3 已知i1=用旋转矢量图求 i=i1+i2。

解 作出与 i1、i2 相对应的旋转矢量 I1、I2，如图3.2.9 所示。应用平行四边形法则求和，即I=I1+I2，由于 I1=I2，并且I1 和I2 与x 轴（图中省略了此基准线）正方向的夹角均为，从图中可以看出x 轴上、下各为一个等边三角形，则I 与I1、I2 相等，即

又由于I 与x 轴正方向一致，即初相位角为 0，从而得到

应当指出，只有正弦量才能用旋转矢量来表示，只有同频率正弦量才能借助于平行四边形法则进行旋转矢量加减运算。

图3.2.9　旋转矢量图