约束与无约束最优解的差异

n维目标函数f（X）=f（x₁，x₂，…，x_n），若在无约束条件下极小化，即在整个n维设计空间寻找X^*=（x₁^*，x₂^*，…，x_n^*）^T，使满足minf（X）=f（X^*），X∈Rⁿ，其最优点X^*、最优值f（X^*）构成无约束最优解；若在约束条件限制下极小化，即在可行域中寻找X^*=（x₁^*，x₂^*，…，x_n^*）^T，使满足minf（X）=f（X^*），X∈Rⁿ，其最优点X^*、最优值f（X^*）构成约束最优解，无论在数学模型还是几何意义上，两者均是不同的概念。

现用一个二维非线性最优化问题，从几何意义上来说明约束最优解和无约束最优解。

设已知目标函数f（X）=x²₁+x²₂-4x₁+4，受约束于g₁（X）=x₁-x₂+2≥0，g₂（X）=x₁≥0，g₃（X）=x₂≥0，g₄（X）=-x²₁+x₂-1≥0，求其最优解X^*和f（X^*）。图2-1a表示其目标函数和约束函数的立体图，图2-1b表示其平面图。当目标函数f（X）=0.25、1、4、6.25时，相应在x₁Ox₂设计平面内得一系列平面曲线（同心圆）——等值线，它表示了目标函数值的变化情况，越向里边的代表目标函数值越小。显然其无约束最优解为目标函数等值线同心圆中心X^*（1）=（x^1*（1），x₂^*（1））^T=（2，0）^T，f（X^*（1））=0。而其约束最优解则需在由约束线g₁（X）=0，g₂（X）=0，g₃（X）=0，g₄（X）=0组成的可行域（阴影线里侧）内寻找使目标函数值为最小的点，由图可见，约束线g₄（X）=0与某等值线的一个切点X^*（2）即为所求，X^*（2）=（x₁^*（2），x₂^*（2））^T=（0.58，1.34）^T，f（X^*（2））=3.8为其约束最优解。

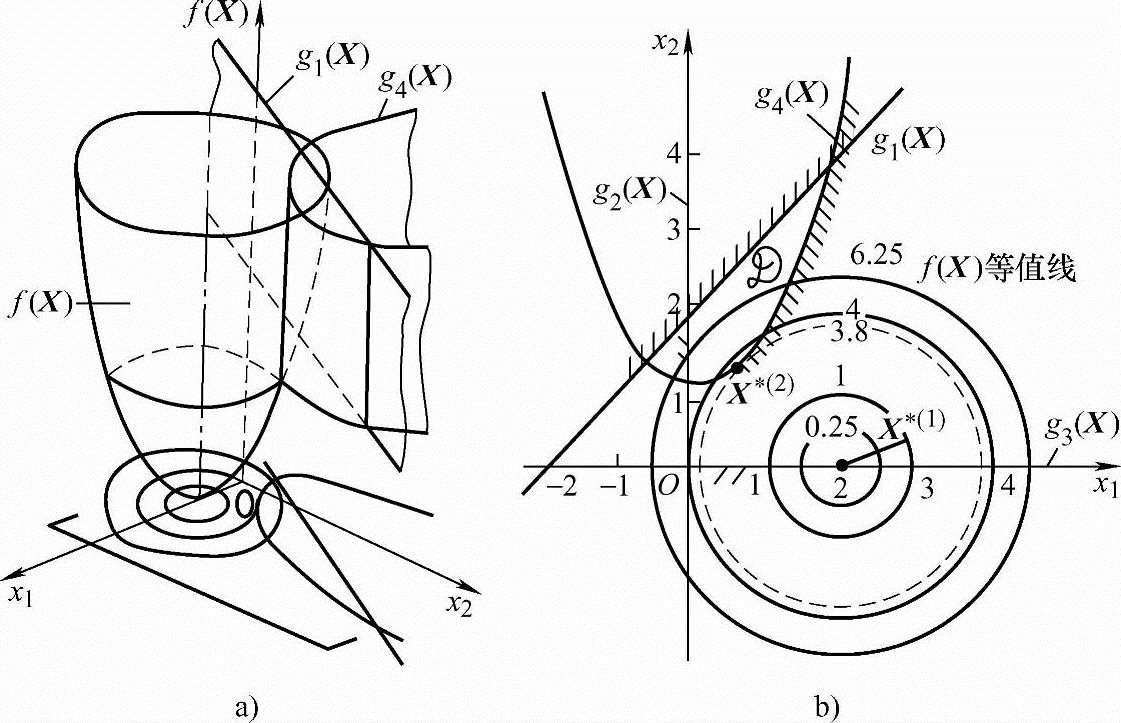
图2-1 二维函数的约束最优解和无约束最优解(www.xing528.com)

以上二维问题关于约束最优解和无约束最优解几何意义的讨论，同样可以推广到多维问题。n个设计变量（x₁，x₂，…，x_n）组成设计空间。在这个空间中的每个点代表一个设计方案。此时n个变量有确定的值。当给定目标函数某一值时，就在n维设计空间内构成一个目标函数的等值超曲面，给定目标函数一系列数值时就得一系列目标函数的等值超曲面。这些等值超曲面反映了目标函数的变化情况。无约束最优点为这些等值超曲面的共同中心。对于约束最优化问题，每一个约束条件在n维设计空间中是一个约束超曲面，全部约束超曲面在设计空间中构成可行域。在其上寻找目标函数值最小的点即为约束最优点。这一点可以是目标函数等值超曲面与某个约束超曲面的一个切点，也可以是目标函数值较小的某些约束超曲面的交点（如图2-2所示的X^*点）。

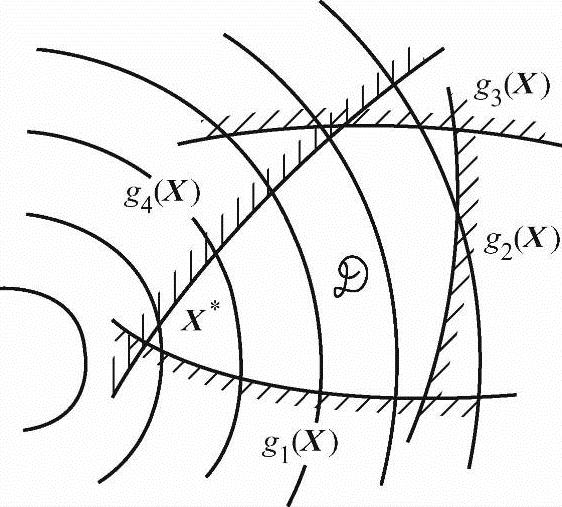
图2-2 n维问题的约束最优点和无约束最优点