例5-5 求约束优化问题
minf(X)=x21+x2
s.t.g1(X)=x21+x22-9≤0
g2(X)=x1+x2-1≤0
的最优解。
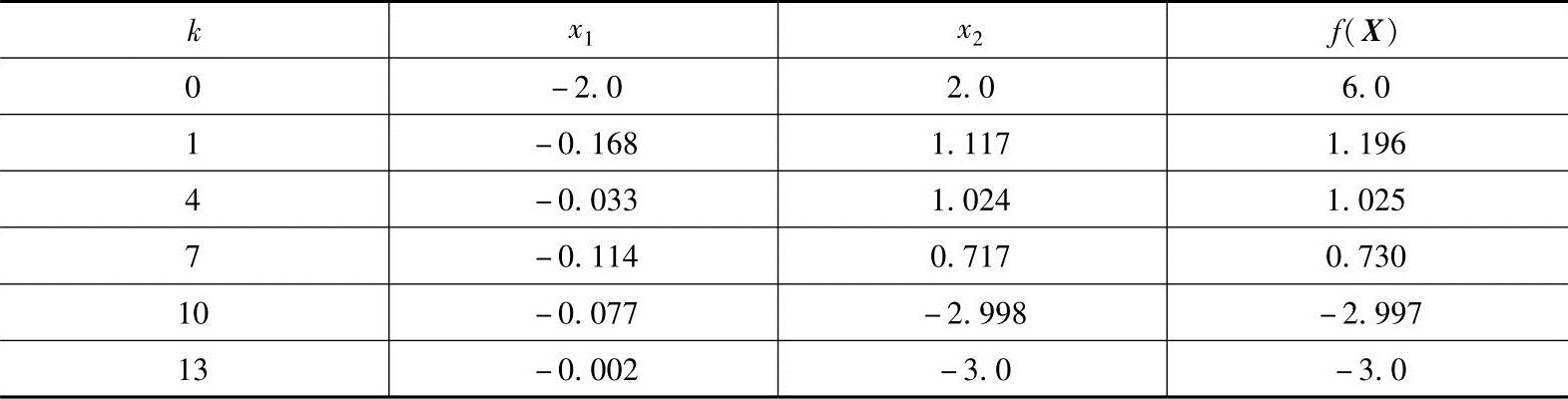
解:用随机方向法程序在计算机上运行,共迭代13次,求得的约束最优解为X*=(-0.002,-3.0)T,f(X*)=-3,计算机计算的结果摘录于表5-1,该问题的图解示于图5-30。
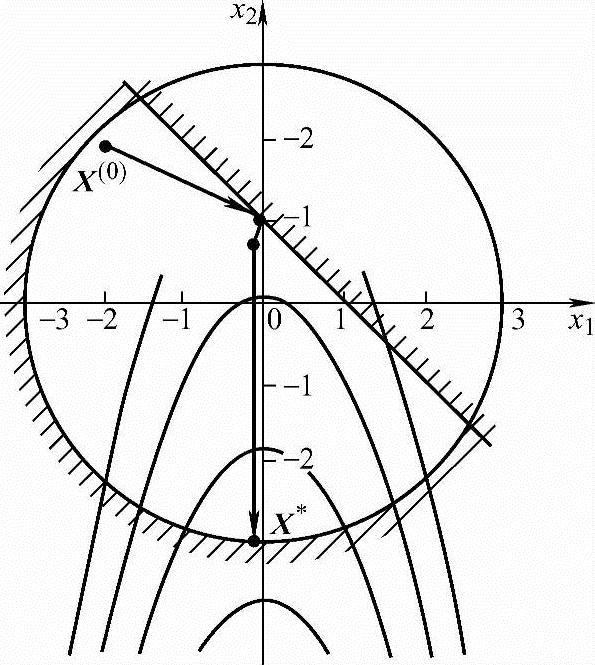
图5-30 例5-5图解
表5-1 例5-5的计算结果
例5-6 用复合形法求约束优化问题
minf(X)=(x1-5)2+4(x2-6)2
s.t.g1(X)=64-x21-x22≤0
g2(X)=x2-x1-10≤0
g3(X)=x1-10≤0
的最优解。
解:用复合形法程序在计算机上运行,共迭代67次。求得的约束最优解为X*=(5.219756.06253)T,f(X*)=0.06393,计算机计算的结果摘录于表5-2,该问题的图解示于图5-31。
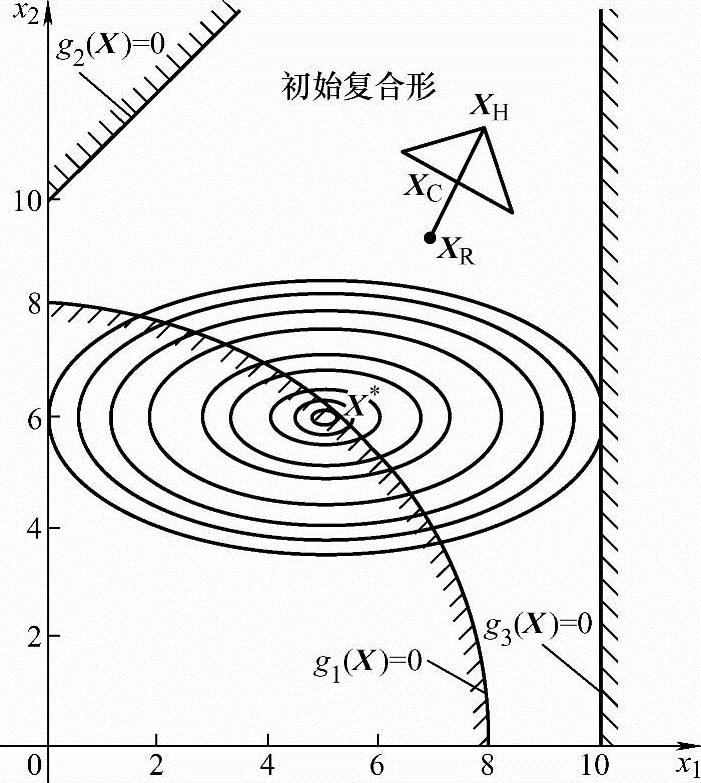
图5-31 例5-6图解
表5-2 例5-6的计算结果

(续)
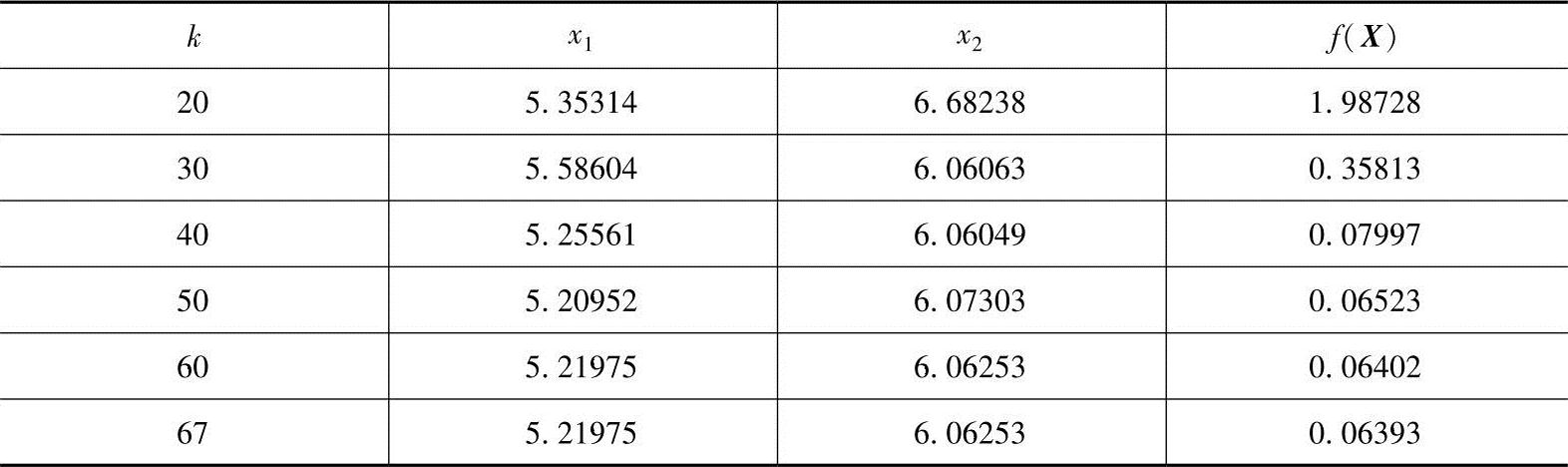
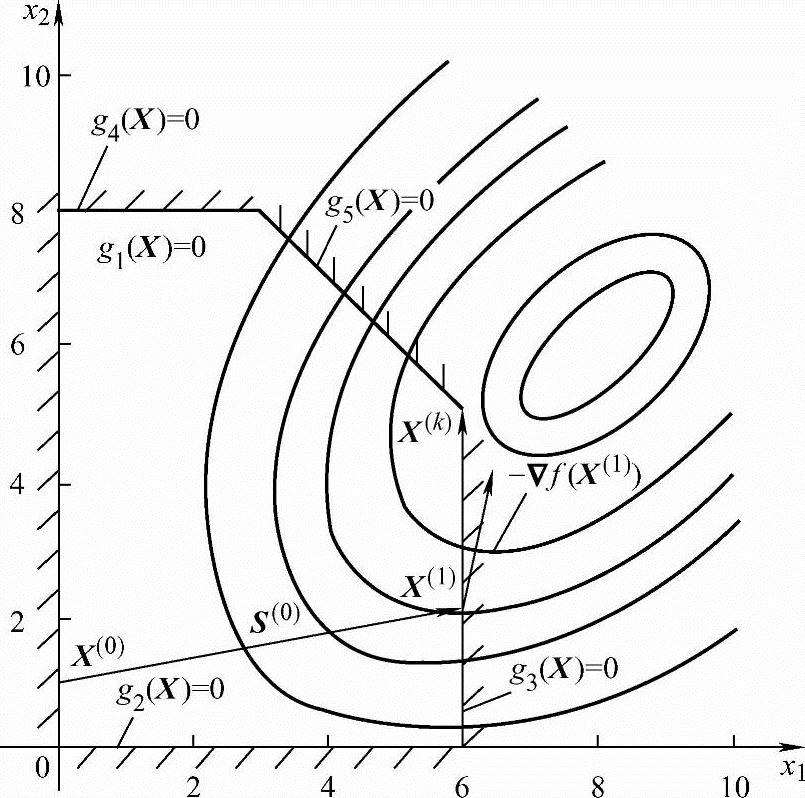
图5-32 例5-7图解
例5-7 用可行方向法求约束优化问题
minf(X)=60-10x1-4x2+x21+x22-x1x2
s.t.g1(X)=-x1≤0
g2(X)=-x2≤0
g3(X)=x1-6≤0
g4(X)=x2-8≤0
g5(X)=x2+x1-11≤0
的约束最优解。
解:为了迸一步说明可行方向法的原理,求解时将先采用优选方向法,后采用梯度投影法来确定可行方向。该问题的图解如图5-32所示。
取初始点X(0)=(0,1)T为约束边界g1(X)=0上的一点。第一次迭代用优选方向法确定可行方向。为此,首先计算X(0)点的目标函数f(X(0))和约束函数g1(X(0))的梯度:
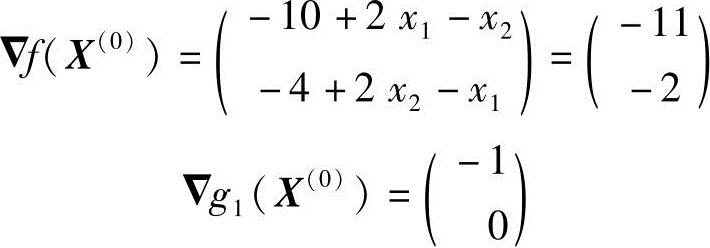
为在可行下降扇形区内寻找最优方向,需求解一个以可行方向S=(S1,S2)T为设计变量的线性规划问题,其数学模型为
min[▽f(X(0))]TS=11S1-2S2(https://www.xing528.com)
s.t.[▽g1(X(0))]TS=-S1≤0
[▽f(X(0))]TS=11S1-2S2≤0
S21+S22≤1现用图解法求解,如图5-33所示,最优方向是S*=(0.984,0.179)T,它是目标函数等值线(直线束)和约束函数S21+S22=1(半径为1的圆)的切点。第一次迭代的可行方向为S(0)=S*,若步长取α(0)=6.098,则
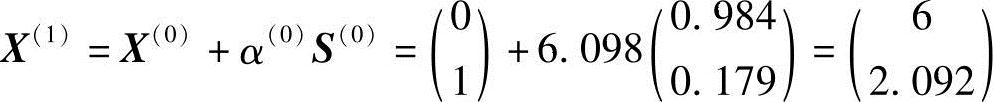
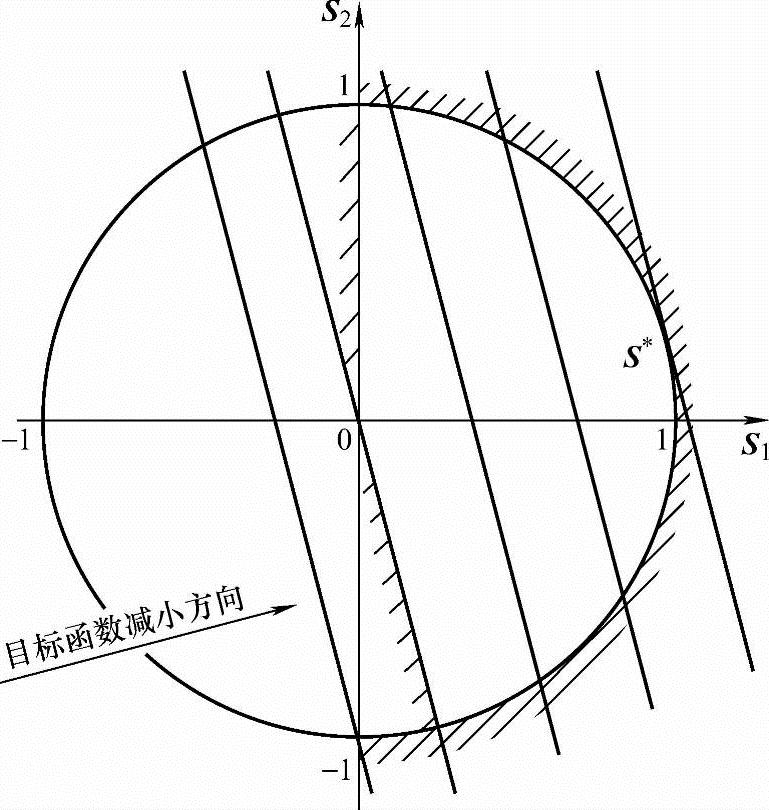
图5-33 用线性规划法求最优方向
可见第一次迭代点X(1)在约束边界g3(X(1))=0上。
第二次迭代用梯度投影法来确定可行方向。迭代点X(1)的目标函数负梯度-▽f(X(1))=(0.092,5.816)T不满足方向的可行条件。现将-▽f(X(1))投影到约束边界g3(X)=0上,按式(5-29)计算投影算子
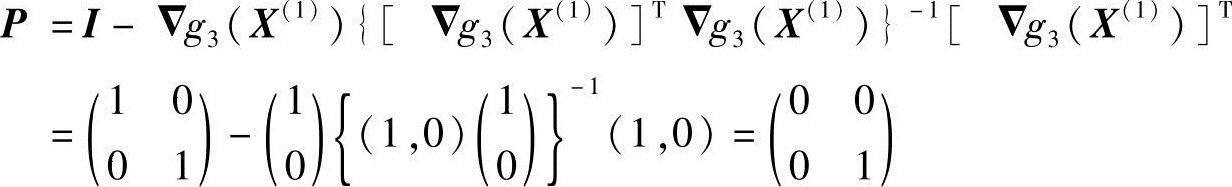
本次迭代的可行方向为
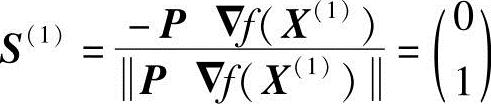
显然,S(1)为沿约束边界g3(X)=0的方向。若取α(1)=2.909,则本次迭代点
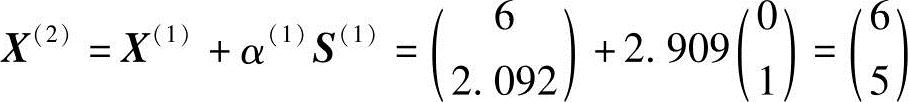
即为该问题的约束最优点X*,则得约束最优解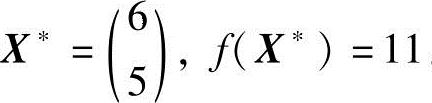 。
。
例5-8 试用混合罚函数法求点集A(x1,x2,x3)和点集B(x4,x5,x6)之间的最短距离。限制条件为
x21+x22+x23≤5
(x4-3)2+x25≤1
4≤x6≤8
分析由图5-34可知x21+x22+x23≤5表示以原点为球心、半径为5的球体,点集A(x1,x2,x3)在球面上取点。(x4-3)2+x25≤1,4≤x6≤8表示一圆柱体,点集B(x4,x5,x6)在圆柱面上取点。因此该问题就是求这两个几何体间的最短距离的约束优化问题,其数学模型为
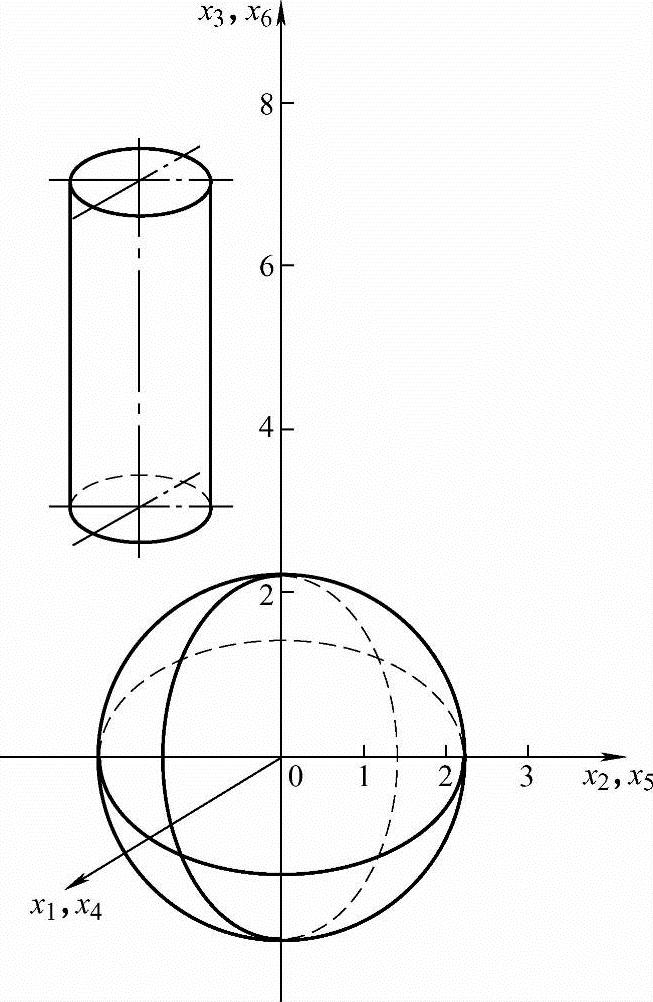
图5-34 例5-8图解
minf(X)=(x1-x4)2+(x2-x5)2+(x3-x6)2
s.t.g1(X)=x21+x22+x23-5≤0
g2(X)=(x4-3)2+x25-1≤0
g3(X)=x6-8≤0
g4(X)=4-x6≤0
解:用混合法程序计算时,取X(0)=(1,1,1,3,1,5)T,R(0)=1,c=0.2在计算机上运行,共迭代13次,求得的最优解为X*=(1.0015,-0.0035,1.999,2.0,0.0077,4.07)T,f(X*)=5.008。和理论解X*=(1,0,2,2,0,4)T,f(X*)=5比较,误差很小。
例5-9 用增广乘子法求问题
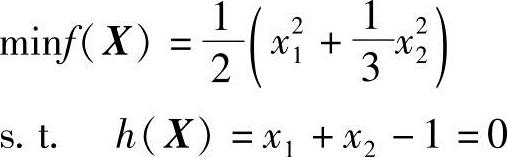
的约束最优解。
解:这个问题的精确解为X*=(0.25,0.75)T,f(X*)=0.125。相应的乘子向量为λ*=0.25。
按式(5-57)构造增广乘子函数
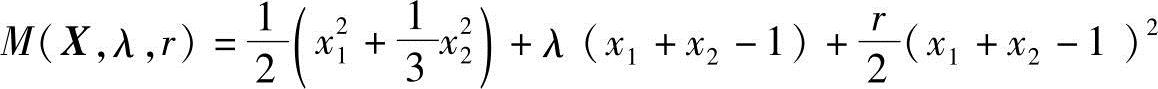
用解析法求M(X,λ,R),即令▽M(X,λ,R)=0可得最优解
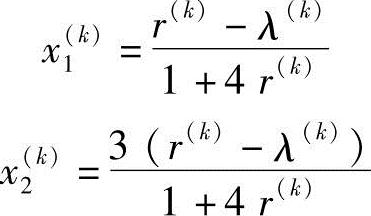
取R(0)=0.1,β=2,λ(0)=0,X(0)=(0.0714,0.2142)T,共迭代6次得到最优解:X*=(0.2499,0.7499)T,f(X*)=0.125,和精确解相比,误差很小。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




