假定在图1.1的系统中,有外力作用在物体上,则物体的运动由方程式(1.2)所决定。外力的形式多种多样,可以是时间的任意函数。这里考虑角频率为ω的简谐外力,F(t)=F0 sinωt,F0为力幅,则方程式(1.2)成为

由定律2可知,首先需找到这个方程的一个特解。由于方程右端是一个正弦函数,可以设该方程的一个特解为x=Xsinωt。代入上式可得
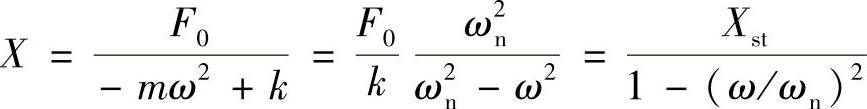
这里,Xst=F0/k表示物体在最大力作用下的静变形。方程式(1.7)所对应的齐次型的通解已由式(1.5)给出,于是,该方程的通解为
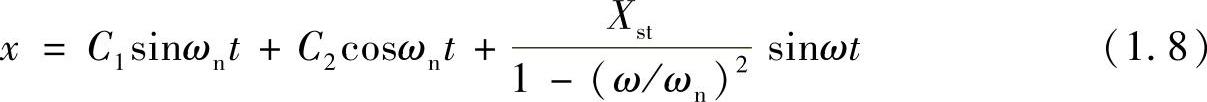
C1、C2为两个由初始条件确定的常数。式(1.8)前两项代表振动频率为固有频率的自由振动成分,第三项则代表与激励力同频率的强迫振动成分。由于有两个独立的频率成分存在,该振动不再是简谐振动。
对于静止的初始条件x(0)=0,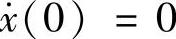 ,可以求得
,可以求得
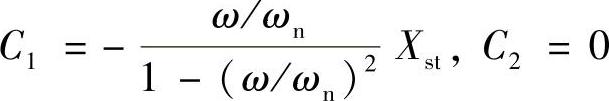
代入式(1.8),可得振动响应为
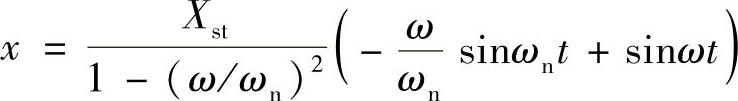
可见,当ω=ωn时,振幅将变为无穷大,这就是通常所说的共振现象。
如图1.5所示为固有频率2Hz的无阻尼单自由度系统在静止的初始条件下,用正弦波激振时的位移响应(在此计算中,调整力幅的大小,使得Xst=F0/k=1mm)。当激振频率为0.5Hz(ω/ωn=0.25)及4Hz(ω/ωn=2)时,位移响应由固有频率与激励频率两个频率成分上的响应合成,振幅一定。当激振频率等于固有频率时(ω/ωn=1),发生共振,振幅越来越大(为了避免被0除的问题,在这个计算中,激励频率约为2Hz)。
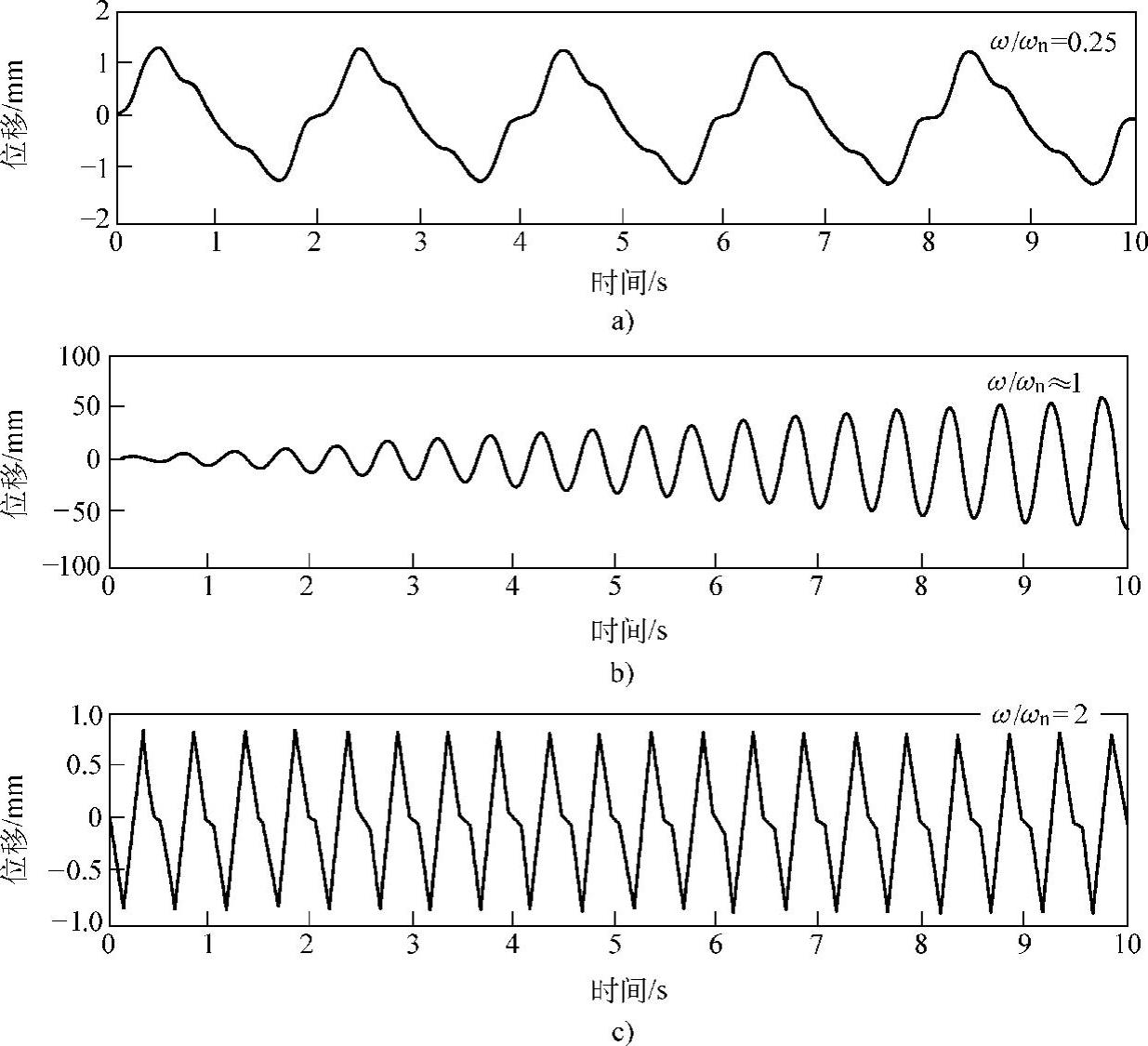
图1.5 固有频率为2Hz的无阻尼单自由度系统的强迫振动响应
a)ω/ωn=0.25 b)ω/ωn≈1 c)ω/ωn=2
在无阻尼的理想状态下,一旦振动发生,将无限地持续下去。实际中,由于阻尼的作用,自由振动项会很快衰减掉,最后只剩下强迫振动的成分,因而我们更关心式(1.8)中的第3项。在此,略去自由振动项,只考虑强迫振动一项,式(1.8)成为

式(1.9)与激振力F(t)=F0 sinωt相比,可得

这是一个随激振频率变化的函数,称为系统的频率响应函数(Frequency Response Function,FRF)。这种从频率响应的角度来考查系统振动特性的方法称为频域分析法。
上式有一个显著的特点,就是当ω=ωn时,分母变为0,响应为无穷大。令
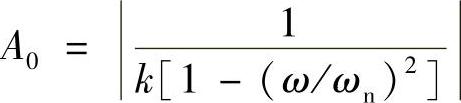 (https://www.xing528.com)
(https://www.xing528.com)
则对于ω<ωn,式(1.10)可以变形为(应用欧拉公式e±jθ=cosθ±jsinθ)
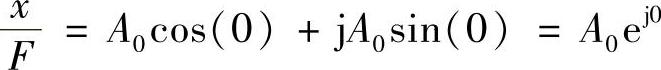
上式表明,位移响应与激振力之间的相位差为0,即二者同相。
同样,对于ω>ωn,式(1.10)可以变形为
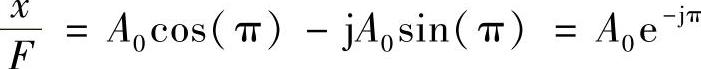
这时,位移与激振力之间的相位差为180°,即二者反相。
应用极坐标表示形式,上述频率响应函数可以写为更一般的形式

A0(ω)称为幅频特性,φ(ω)称为相频特性。我们把上述位移与激励力之间的传递函数H(ω)称为柔顺性函数(Compliance)。相应地,把速度与激励力之比称为导纳函数(Mobility),加速度与激励力之比称为惯量函数(Inertance)。
如图1.6所示为根据式(1.10)绘制的幅频响应曲线及相频曲线。这里,共振时刻(激振频率为2Hz)的相位取为-90°(理由参照图1.7)。相对于相频特性,更重要的是幅频特性。当激振频率接近于0Hz时,幅值为一常数,等于弹簧刚性系数的倒数,即柔性系数,用于衡量静力作用下的变形。当激振频率远大于共振频率时,幅值变得很小,最终趋近于0。这是因为激振力变化太快,物体由于惯性的影响跟不上力的变化,结果是原地不动。
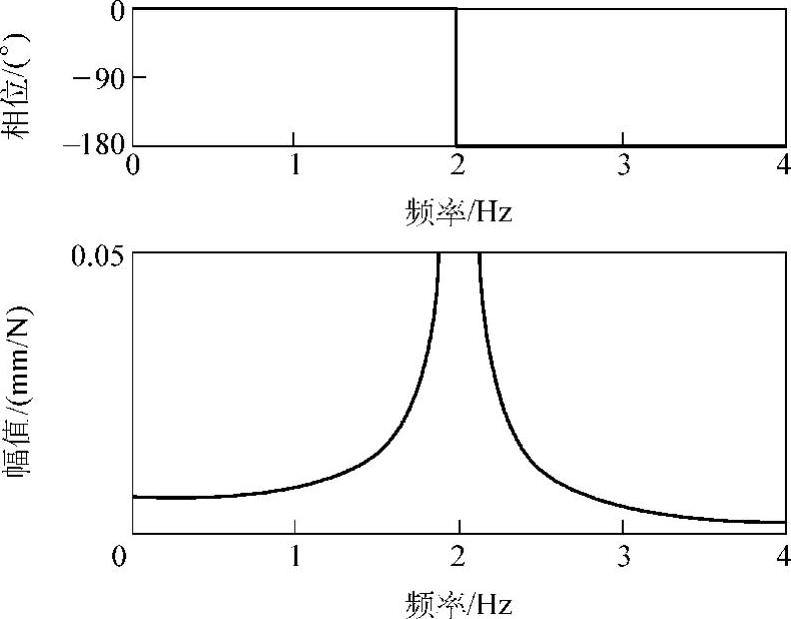
图1.6 无阻尼单自由度系统的频率响应曲线
我们知道,当一个静态力(不随时间变化或变化很慢,即频率为0或接近于0)作用在结构上时,结构将产生变形,变形的大小由力的大小和结构的刚性所决定。而当一个动态力(随时间较快变化)作用在结构上时,此时的变形不但取决于力的大小和刚性值,而且与激励力的频率及结构的固有频率有关。当发生共振时,产生的变形将远远大于同样大小的静态力引起的静变形,很可能使结构发生破坏。因此,掌握并优化产品的动态特性,以避免发生共振对于设计工程师来说非常重要。
在此,引入动刚性的概念。动刚性为柔顺性函数的倒数,也是频率的函数;频率为0时,所对应的值就是静刚性。共振时,动刚性最小(对于这里所讨论的无阻尼共振,动刚性为0);频率大于共振频率以上,随着频率的增加,动刚性越来越大。
相对于以上频域分析,如图1.5所示在时间轴上观察振动特性的方法称为时域分析。这里,我们再来看一个时域分析的例子。图1.7是在初始条件为0的条件下对上述单自由度系统(固有频率为2Hz)用扫描正弦力进行激振的结果。在0~5s的时间里,激振频率由0Hz变为4Hz。在2.5s的时候,频率为2Hz,发生共振。图中清楚地显示,共振之前,位移和激振力同相,而在共振之后,位移和激振力反相。在共振时刻(t=2.5s),位移为最大,而激振力刚好为0,二者成90°相位差的关系。
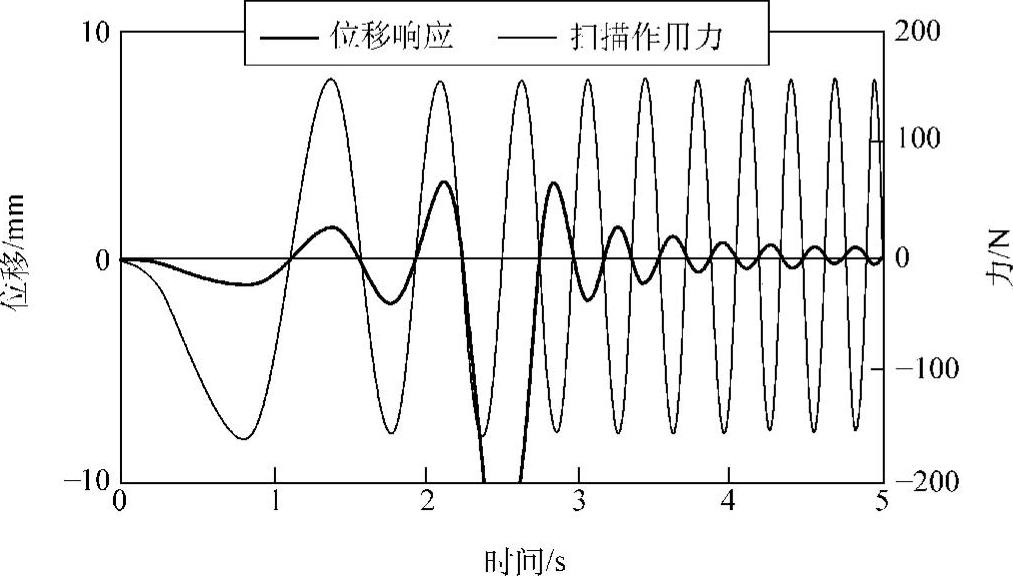
图1.7 正弦扫描激振时的位移响应及激振力
最后,作为参考,这里给出上述计算中所使用的扫描正弦的定义
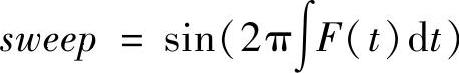
其中,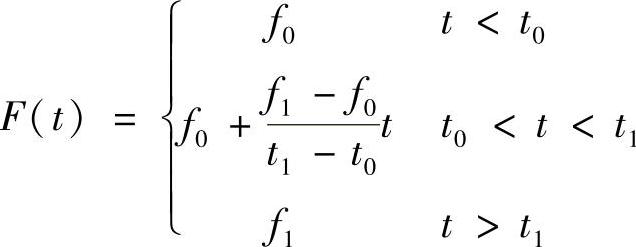 ,在时间段(t0,t1)上,频率由f0变为f1,则有
,在时间段(t0,t1)上,频率由f0变为f1,则有
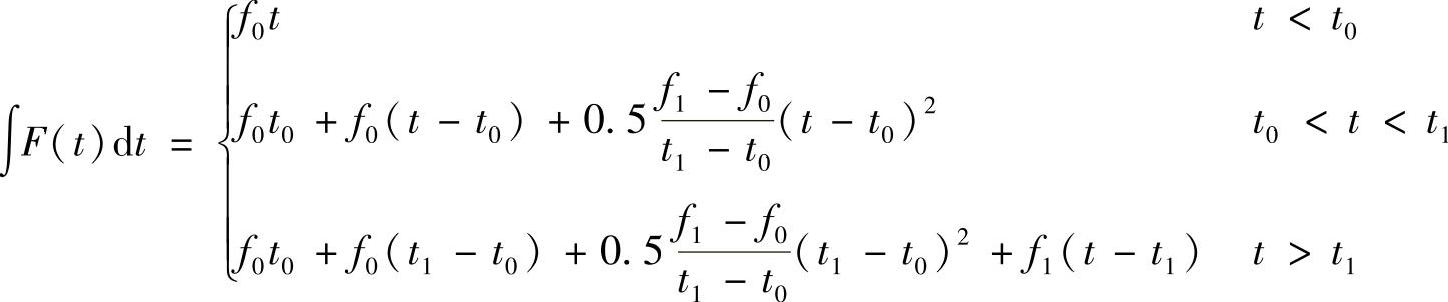
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




