高效的Lanczos算法优化方案

前面我们说过，矩阵特征值问题的解法可以分为迭代法和相似变换法。迭代法的特点是每求解一个特征值（或特征向量）时，都要利用迭代运算，而且每次迭代运算只能得到一个特征值（或特征向量）；相似变换法则是通过相似变形把原有矩阵转化为对角阵，从而一举得到所有的特征值及特征向量。尽管在Jacobi法或Househoulder-QR法中，都用到了相似变形的反复递推运算（也叫做迭代），但本质上不属于迭代解法。

把相似变形法与迭代法的长处结合起来的特征值解法称为混合方法，代表方法就是Lanczos法。Lanczos法的原理是基于Lanczos变换。Lanczos变换也是一种把对称矩阵转换为3重对角矩阵的方法，但是在实际计算中，这个变换中所用的正交变换矩阵易于受到数值舍入误差的影响，从而达不到所期望的正交化效果。所以，作为相似变形方法来求解全部的特征值和特征向量，Lanczos变换的效果不如House-holder变换。但是，如果我们的目标是求解一部分特征值和特征向量（这是结构动力学分析的一般情况），则基于Lanczos变换的迭代解法的计算效率非常高。因此，在当今的大规模有限元动力学分析当中，Lanczos法已成为求解固有值问题的最重要方法之一。

1.Lanczos变换

实对称矩阵A经过相似变形成为3重对角阵B，则有

这里，P为正交矩阵，P=[x₁x₂…x_n]，x_i（i=1，…，n）为P的列向量，并且各个向量间正交，即x^T_ix_j=0，i≠j。根据正交矩阵的性质，可得AP=PB，即

将上式展开，得到下列关系

为了确定参数α_i，求Ax_i与x_i的内积并注意到可得，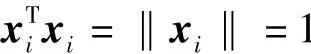

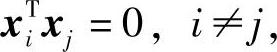
α_i=x^T_iAx_i（5.81）

此外，根据Ax_i=β_i-1x_i-1+α_ix_i+β_ix_i+1定义一个新的向量

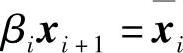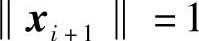则。由于，可得

这样，最初选一个‖x₁‖=1的x₁，利用式（5.81）～（5.84），就可以求出所有的参数α_i、β_i。也就是说，可以得到3重对角矩阵。

对于结构动力学中的一般化特征值问题，Kφ=λMφ，上述Lanczos变换把它转化为一个3重对角矩阵的标准特征值问题。其过程如下：

最初选一个起始向量x，为了用模态质量进行正规化，定义

考虑到最终的目的是使K变为对角阵，M变为单位阵（Φ^TKΦ=Λ，Φ^TMΦ=I），可以按以下步骤依次进行计算（β₀=0，i=1，…，n）

从而得到正交矩阵P_n=[x₁x₂…x_n]。理论上，这个矩阵使得M变为对角阵，并且

为了证明上式，对式（5.85）做以下变形

整理得

考虑i=1，…，l的情况，利用上式，可以列出l个方程并整理成以下形式(www.xing528.com)

即

这里，P_l为n×l矩阵，e_l是长度为l的列向量

e^T_l=[0…01]

给式（5.87）两边同乘以P^T_lM，并利用正交性质，可得

T_l=P^T_lMK^-1MP_l （5.88）当l=n时，就是式（5.86）。

现在来考察如何把Kφ=λMφ变为标准特征值问题。给Kφ=λMφ两边都左乘以K^-1，再左乘以M可以变形为

令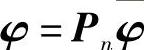，代入上式后，给两边都左乘以P^T_n，并利用P^T_nMP_n=I，可得

可见，一般化特征值问题Kφ=λMφ可以转化为式（5.89）所示的标准特征值问题。二者之间的特征值互为倒数，特征向量由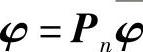联系起来。

2.Lanczos迭代法

以上变换是在没有数值舍入误差的理想情况下进行的，得到的正交矩阵严格满足正交条件。但事实上，Lanczos变换易受数值舍入误差的影响，导致该方法作为一举求出所有特征值与特征向量的相似变形法效果并不理想。但是，如果我们仅需要低阶少数的特征值与特征向量，则利用Lanczos变换可以推演出一个高效的迭代方法。

事实上，式（5.85）表示的是一个类似于逆迭代法的过程。如果我们考虑正交向量的子集，i=1，…，q（q<<n），则可以得到（注意：T_q直接由α_i，β_i组装而成）

并构建一个新的特征值问题

T_qθ=γθ （5.91）

式（5.91）的特征值γ是对式（5.89）所代表的特征值的近似，由长度为q的特征向量θ也可以得到式（5.89）的特征向量的近似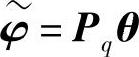。由于式（5.91）的规模远远比式（5.89）的规模要小（q<<n），求解效率非常高（小规模3重对角矩阵的QR变换），这就是Lanczos迭代法的优点。显然，q越大，结果越接近于原有问题的特征值。至于何时结束上述迭代过程，由误差判定准则决定。

例如假定求原有问题Kφ=λMφ的l个低阶特征值，先在q=2l上进行Lanczos变换得到T_2l，求解并考察它的l个高阶特征值（对应于原有问题的l个低阶特征值）；如果不满足精度要求，再在q=3l上进行Lanczos变换，得到T_3l，并求其l个高阶特征值。重复这个过程，直到满足精度要求为止。

具体的迭代算法为了提高精度、稳定性和计算效率，还要结合使用Gram-Schmidt正交化方法、移位技术（shifting）、Sturm序列等方法，这里不做深究。