循环码生成：多项式、矩阵与原理

1.循环码的生成多项式和编码原理

由定理6.34知，（n，k，d）循环码中的每个码多项式c（x）可以表示成

c（x）=m（x）g（x）=（m₀+m₁x+…+m_k-1x^k-1）g（x）

设m（x）的系数m₀，m₁，…，m_k-1是待编码的k个码元的信息组，则c（x）就是相应的码多项式。因此，用g（x）乘信息多项式m（x）就完成了编码。所以，（n，k，d）循环码完全由次数最低的根据式（6.55）给出的非0码多项式g（x）所决定。为此，引出下面定义：

定义6.61 称（n，k，d）循环码C中唯一的n-k次首一码多项式g（x）为码的生成多项式。

显然，（n，k，d）循环码的生成多项式g（x）的次数等于码中一致校验元的数目n-k。下面定理给出循环码的另一些重要性质：

定理6.35 GF（q）上（n，k，d）循环码的生成多项式g（x）是xⁿ-1的因式。

证明 用x^k乘g（x）得到次数为n的多项式x^kg（x），用xⁿ-1除x^kg（x）得

x^kg（x）=（xⁿ-1）+g^（k）（x） （6.56）

这里g^（k）（x）是余式。由式（6.49）可知g^（k）（x）是g（x）循环右移k次得到的多项式。因而，g^（k）（x）是g（x）的倍式，即g^（k）（x）=a（x）g（x）。则式（6.56）可以改写为

xⁿ-1=[x^k-a（x）]g（x）

因此，g（x）是xⁿ-1的因式。

【证毕】

定理6.36 若g（x）是n-k次多项式且是xⁿ-1的因式，则g（x）生成一个（n，k，d）循环码。

实际上，定理6.36给出了构造循环码的方法。xⁿ-1的任何一个n-k次因式，均可以生成（n，k，d）循环码。对于大的n值，xⁿ-1可以有多个n-k次因式。它们中的某些多项式生成好码，而某些多项式则生成坏码。如何选择生成多项式以得到好的循环码，是一个非常困难的问题。

目前，已发现了许多类好的循环码，并且它们是可以实现的。

【例6.40】

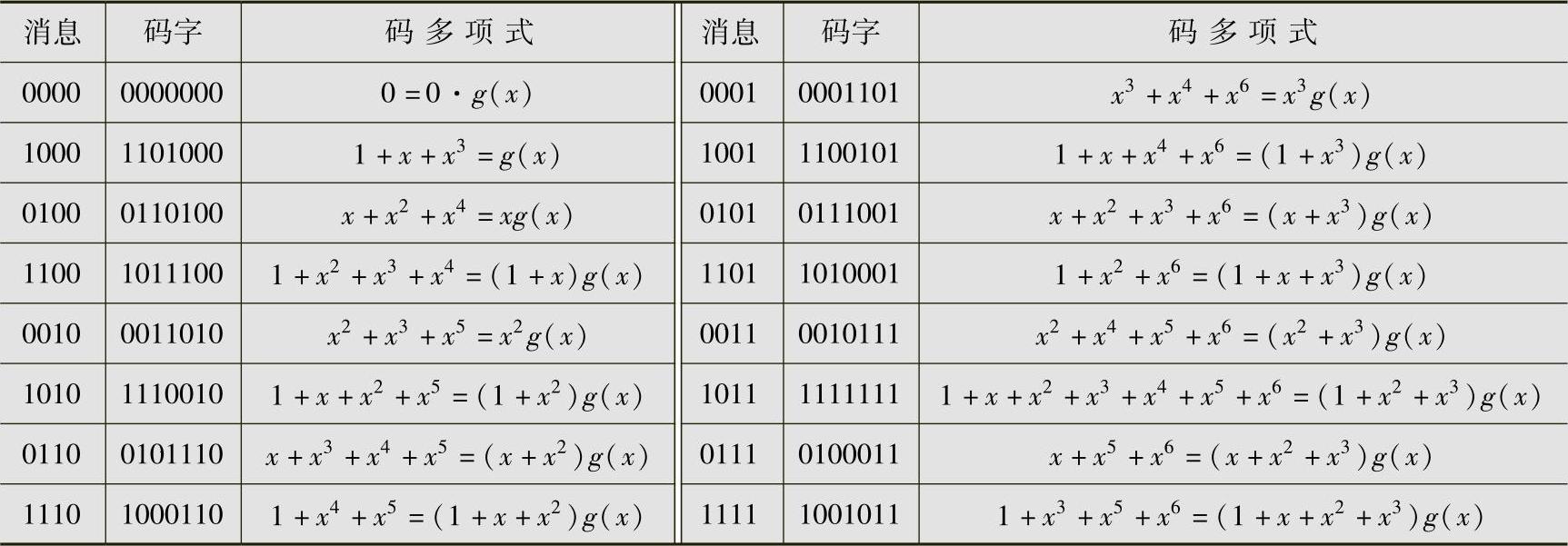
二元（7，4，3）循环码的生成多项式是g（x）=1+x+x³。表6.8给出了该码的全部码多项式，每一码多项式皆是g（x）的倍式。该码是非系统码。

表6.8 用g（x）=1+x+x³生成的（7，4，3）循环码

【例6.41】

GF（2）上多项式x⁷+1可以分解成因式形式

x⁷+1=（1+x）（1+x+x³）（1+x²+x³）

故x⁷+1的全部因式为1个1次因式1+x、2个3次因式1+x+x³和1+x²+x³、2个4次因式（1+x）（1+x+x³）=1+x²+x³+x⁴和（1+x）（1+x²+x³）=1+x+x²+x⁴，以及1个6次因式（1+x+x³）（1+x²+x³）=1+x+x²+x³+x⁴+x⁵+x⁶。由定理6.36知，二元7长循环码仅存在由g（x）=1+x生成的（7，6，2）循环码（也是偶校验码）；由g（x）=1+x+x³和g（x）=1+x²+x³生成的两种（7，4，3）循环码（也是Hamming码）；由g（x）=1+x²+x³+x⁴和g（x）=1+x+x²+x⁴生成的两种（7，3，4）循环码；由g（x）=1+x+x²+x³+x⁴+x⁵+x⁶生成的（7，1，7）循环码（也是重复码）。不存在（7，2）和（7，5）循环码。

2.循环码的生成矩阵

考虑生成多项式为g（x）=g₀+g₁x+…+g_n-k-1x^n-k-1+x^n-k的（n，k，d）循环码。在6.5.1节中已证明k个码多项式g（x），xg（x），…，x^k-1g（x）张成循环码C。若把对应于这k个码多项式的k个n维矢量作为k×n阶矩阵的k行，则得到如下的（n，k，d）循环码C的k×n阶生成矩阵G：

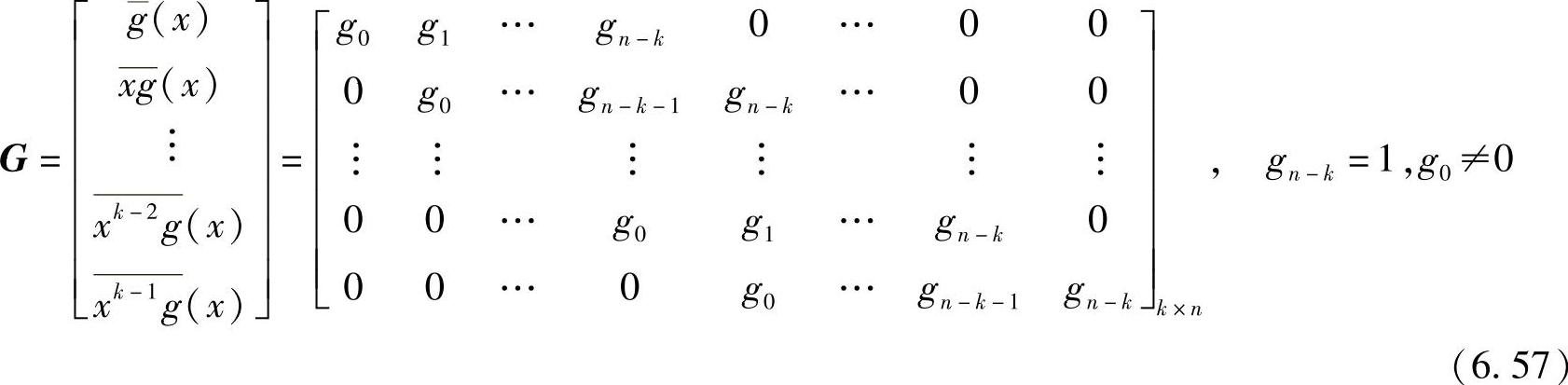
式中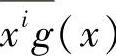，表示由xⁱg（x）的系数组成的行矢量。通常，G不是系统码的生成矩阵。

【例6.42】

二元（7，4，3）循环码的生成多项式为g（x）=1+x+x³，其生成矩阵为

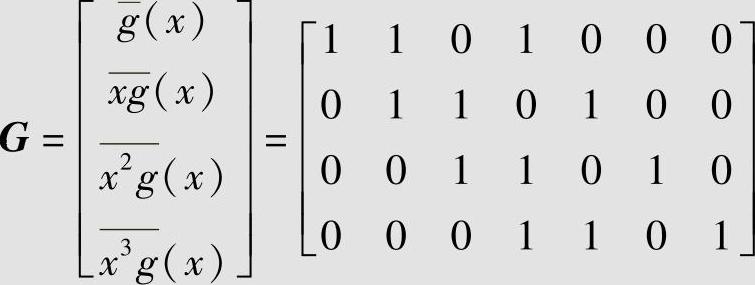(www.xing528.com)

由G可以生成表6.8中给出的（7，4，3）循环码的所有码字。

3.系统循环码的编码方法和系统码的生成矩阵

式（6.57）的生成矩阵G生成的循环码是非系统码。而（n，k，d）系统循环码的生成矩阵应该具有式（6.38）的形式，即G=[P I_k]，其中矩阵P是由生成多项式g（x）确定的GF（q）上k×（n-k）阶矩阵。因为G中的行矢量是码字，所以式G=[P I_k]表明，码多项式的第n-1～n-k次的系数是信息元，其余的为校验元，这相当于

c（x）=r（x）+x^n-km（x）≡0（mod g（x）） （6.58）

式中，m（x）是信息多项式，m（x）=m₀+m₁x+…+m_k-1x^k-1，m=（m₀，m₁，…，m_k-1）是信息元；r（x）是校验多项式，r（x）=r₀+r₁x+…+r_n-k-1x^n-k-1，相应的系数是码字的校验元。由式（6.58）得

r（x）=c（x）-x^n-km（x）≡-x^n-km（x）（mod g（x）） （6.59）

所以，要构造用g（x）生成的（n，k，d）系统循环码，其算法步骤如下：

1）计算x^n-km（x）。

2）用g（x）除-x^n-km（x）得到余式r（x）。

3）系统码的码字为c（x）=x^n-km（x）+r（x）。

可见，（n，k，d）系统循环码编码的核心问题是以g（x）为模的除法问题。

【例6.43】

考虑由g（x）=1+x+x³生成的二元（7，4，3）系统循环码。令m（x）=1+x²是待编码的信息多项式。用g（x）除x³m（x）=x³+x⁵，得到余式r（x）=x²。因此，码多项式是c（x）=r（x）+x³m（x）=x²+x³+x⁵，而对应的码字为c=（0011010），其中最右边的4位是信息组。二元（7，4，3）系统形式的循环码的16个码字列于表6.9中。

表6.9 用g（x）=1+x+x³生成的（7，4，3）系统循环码

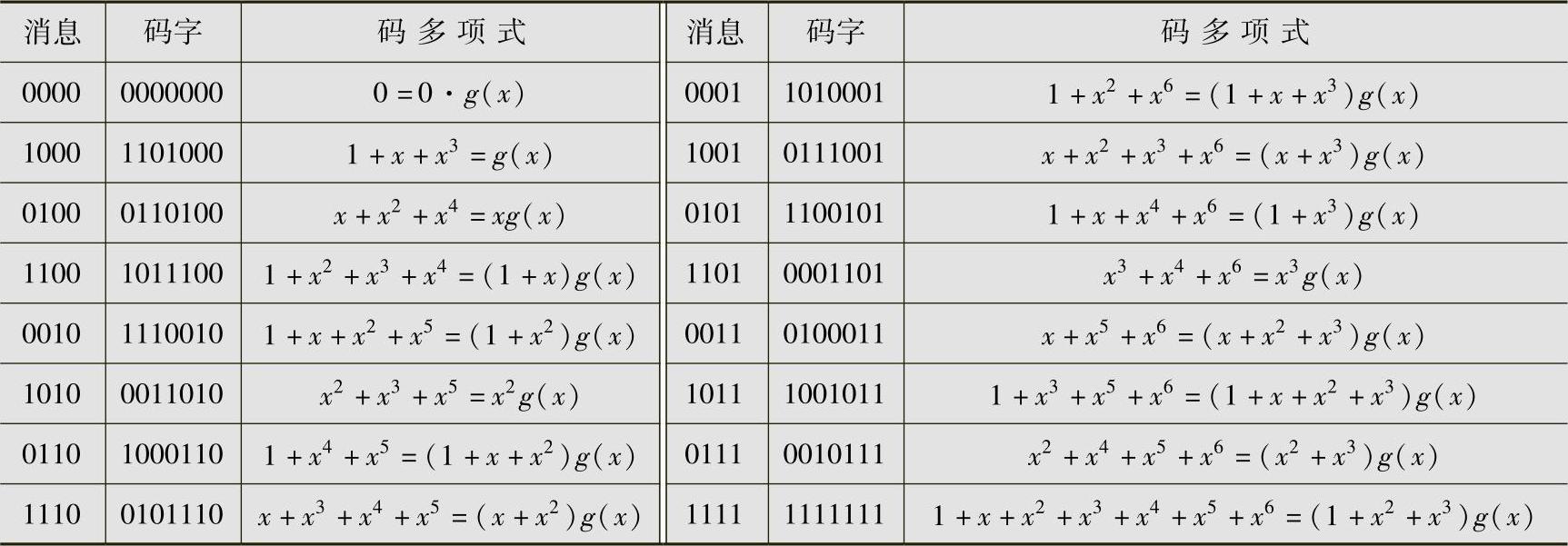
由（n，k，d）系统循环码的生成矩阵G=[P I_k]知，其基底矢量中相对应的信息多项式分别为m₀（x）=1，m₁（x）=x，…，m_k-1（x）=x^k-1。与这些信息多项式相对应的校验多项式分别为r₀（x）≡-x^n-k（mod g（x）），r₁（x）≡-x^n-kx（mod g（x）），…，r_k-1（x）≡-x^n-kx^k-1（mod g（x））。一般写成

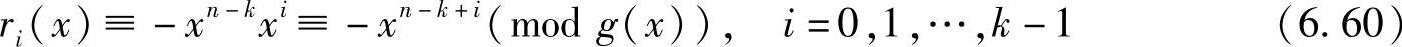
与此相应的码多项式为

以式（6.61）的k个码字作为基底矢量就组成了（n，k，d）系统循环码的生成矩阵，可以表示为

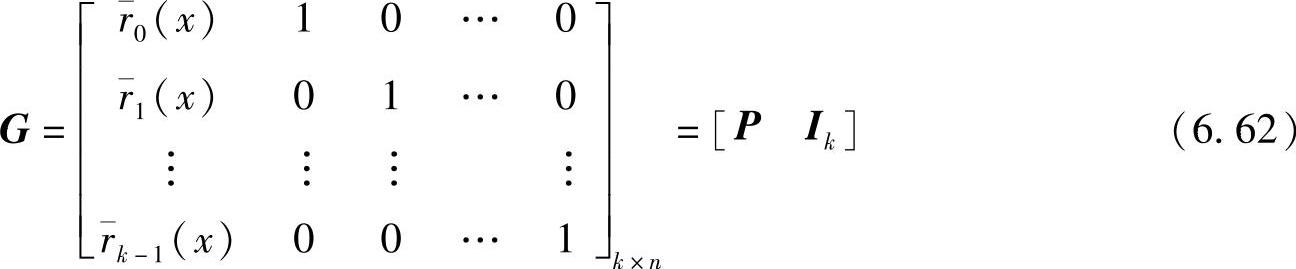
式中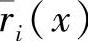，（i=0，1，…，k-1）表示由r_i（x）的系数组成的行矢量。

对于（n-l，k-l，d）缩短循环码，依据定义6.60和式（6.62），不难得到其系统码形式的生成矩阵为

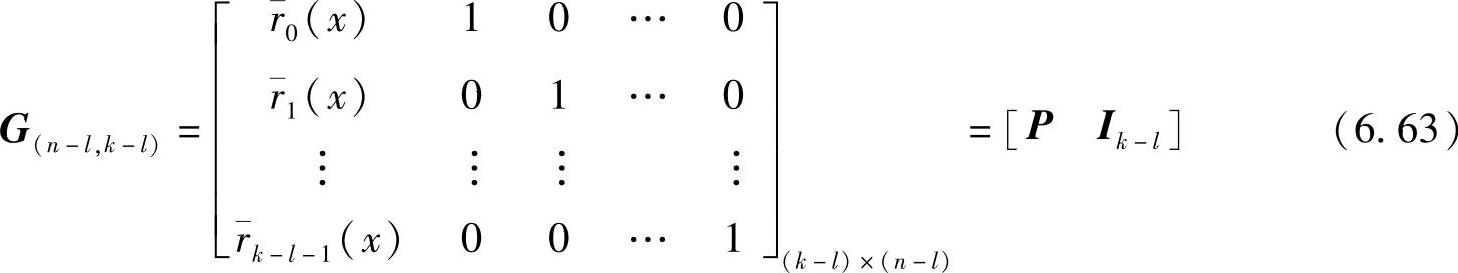
【例6.44】

二元（7，4，3）循环码的生成多项式为g（x）=1+x+x³。计算r₀（x）≡-x³≡1+x（mod g（x）），r₁（x）≡-x⁴≡x+x²（mod g（x）），r₂（x）≡-x⁵≡1+x+x²（mod g（x）），r₃（x）≡-x⁶≡1+x²（mod g（x））。由式（6.62）知，系统形式的生成矩阵为

该码缩短两位得到（5，2）缩短循环码，由式（6.63）知其生成矩阵为

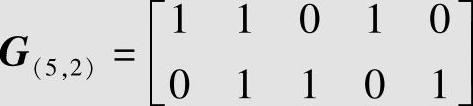
用例6.44的生成矩阵G可以生成表6.9所示的（7，4，3）系统循环码，而用例6.42的生成矩阵G可以生成表6.8所示的非系统循环码。应该指出，这两种循环码是相同的，只是信息组与码字的对应关系不同。