奈奎斯特率采样：最经济的采样方法

在采用定理的描述中，请注意我们一般都说的是f_p>2f_c，这是有原因的。因为如果F（f_c）≠0，或者F（-f_c）≠0，若刚好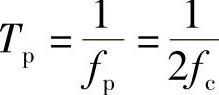，则采样后得到的信号频谱中两个重复片段刚好连在一起，相连的那个边界点，比如f=f_c处的频谱值会相互叠加，从而随后用截止频率滤波时（此时，只能用截止频率滤波），滤出来的频谱相对于原信号的频谱F（f）来说，在边界点f=f_c或者f=-f_c处频谱值失真，如图4-6所示。因此，从严格数学意义上来说，重建的信号不是原信号f（t）。但如果F（-f_c）和F（f_c）都等于0，叠不叠加都无所谓了。所以，只有特殊情况，比如当F（f_c）=F（-f_c）=0时，采样间隔才能刚好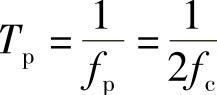取且取，即刚好以奈奎斯特率采样才能严格数学意义上还原原信号。

图4-6 边界点频谱失真

不过纠结于这个意义严格来说不是很大，虽然我们一般说一个信号的频谱主要是指频谱值不为0的那个区间，但是我们也总是可以把这个区间说得稍大一点，也即包含一点频谱值为0的区域，也没啥问题。比如信号f（t）频谱值不为0的那个区间是-W≤ω≤W，我们一般会说信号f（t）是频谱在[-W，W]上的信号，但是我们也可以说信号f（t）是频谱在[-W-ω₀，W+ω₀]，ω₀>0上的信号，也没什么错误。并且对于这种情况，为了方便描述，我们称之为“虚拟”频谱区间。显然，如果我们这样看，则任何信号f（t）的频谱我们基本上都可以看成是两个端点（边界点）的频谱值等于0的频谱，从而都可以说能以奈奎斯特率采样。

注意，当刚好以奈奎斯特率采样时，在表达式（4-15）中

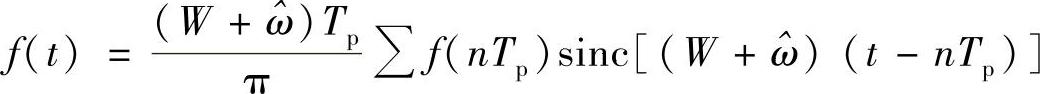
有ω_p=2W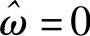，。那么，

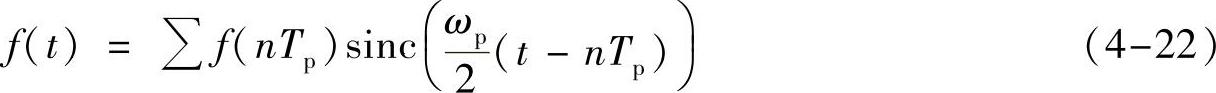
另一方面，注意到

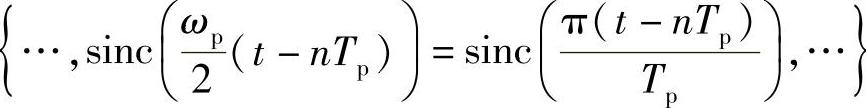
是一组正交基，那么刚好以奈奎斯特率采样的情况说明这样的f（t）能用这组正交基来表示，并且f（t）在这组基下的坐标就是且只能是f（nT_p）。然而，我们又说了，其实任何信号都可以在某种意义下说成是刚好以奈奎斯特率采样，那么也就是任何信号都可以由某组sinc信号正交基表示，仅仅sinc信号正交基的宽度不一样而已（因为采样间隔T_p不一样）。不过需要提醒的是，对于按“虚拟”频谱区间进行奈奎斯特率采样的那些信号，在滤波还原时，需要采用“虚拟”截止频率滤波才行，也即相对于“虚拟”频谱区间的截止频率滤波，而不是实际非零频谱区间的截止频率滤波。图4-7示意了按“虚拟”频谱区间-W-W₀≤ω≤W+W₀进行“虚拟”截止滤波的情形。

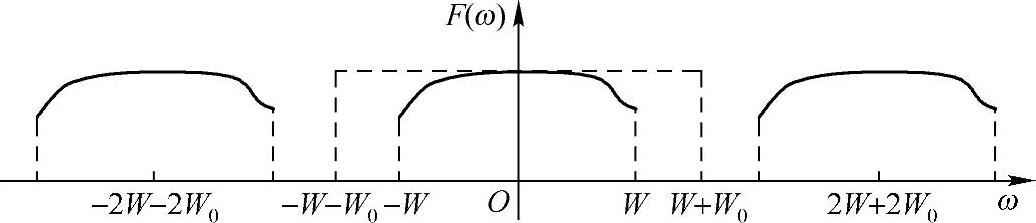
图4-7 “虚拟”截止频率滤波

然而，当刚好以奈奎斯特率采样（可以包含以“虚拟”频谱区间来处理的情形）和按“虚拟”截止频率滤波两个条件至少一个不满足时（前者决定T_p，后者决定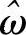），由前面定理2-4中关于sinc信号正交基的讨论，我们知道一般情况下，

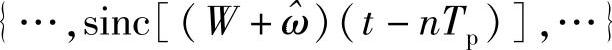
并不是一组正交基，虽然这些情况下，f（t）仍可以由采样点表示出来，但是sinc信号前面的系数并不唯一，即是说采样点序列换成其他序列仍然成立。

提醒

不过强调一下，这里说的是换成其他序列，不是说换成其他采样点序列。显然，相同位置采样，采样点序列都变了，信号当然是不同的信号了。

1.采样偏差影响(www.xing528.com)

上面讲的采样序列是过坐标原点的，即在原点处有采样，整个采样序列相对于原点偏移会怎样？根据上面的推导，重新按偏移情况写一遍，留做练习。

另一方面，现实中的时间是绝对的，但在描述信号时，一般是用的相对时间坐标，即按照需要自己设定原点在哪儿。当设定好一个原点，按照过原点的采样序列采样，就是上面的推导；如果对同一个信号，用相对于原点偏移的采样点序列来采样，觉得不好理解，则你可以把原点重新设定在某个偏移后的采样点上，那又满足上面的推导了，即偏移后的采样序列也能唯一还原重新设定原点的信号。注意，不管我们把原点设定在哪儿，被采样的信号实质是没变化的，那就是说不管采哪些点，只要采样间隔大于奈奎斯特率就行了。

思考一下

对信号sinc（t）自身应用采样定理，观察一下有什么有趣的发现？

前面，我们弄出了傅里叶级数或傅里叶变换，我们就想去看看信号的其他特征，如功率，能量等，在新的形式下是个什么样子。现在弄出了采样定理，它和信号功率，能量等又有什么关系呢？

性质4-1（采样点与信号能量关系）假设按间隔T采样对于信号f（t）来说是满足采样定理的，即f（nT）是对f（t）按大于（或等于）奈奎斯特率采样得到的采样点，那么信号的能量

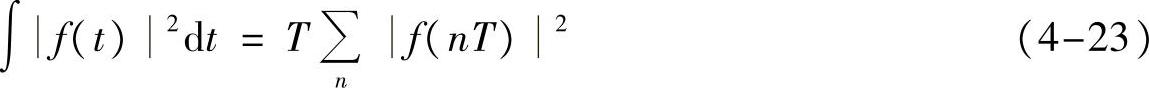
或者，信号的功率

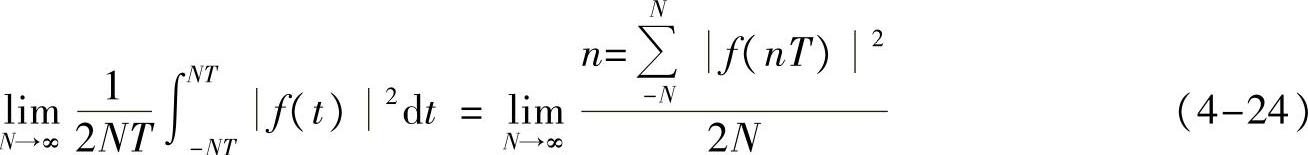
证明 只要是满足采样定理，那我们就一定可以用（“虚拟”）截止频率滤波还原，即信号f（t）总是可以写成

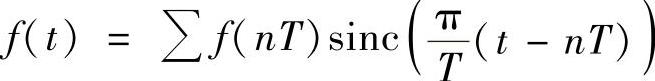
注意到此时{…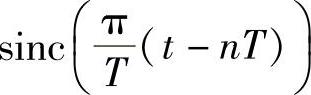，，…}是一组正交基，同样由模与坐标的关系可得

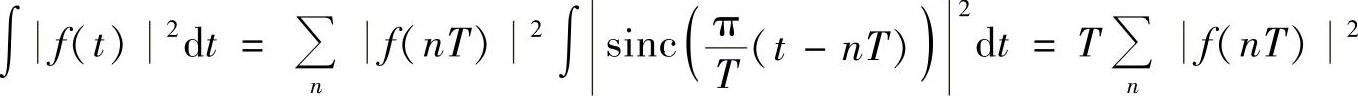
能量部分得证，功率部分显然。

这个结论很有意思，一些直观的事实，在满足采样定理的条件下，采样点增加，显然采样点的平方和就增大，但注意到此时，采样间隔T在变小，最后的总效果是保持不变，都等于信号的能量。更有意思的是，当采样间隔T→0时，有

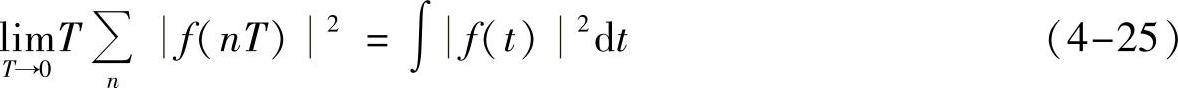
这不就是信号能量的定义嘛。

最后，线性空间知识（基，坐标）在前面的傅里叶级数和傅里叶变换等推导中，似乎是万能灵药一样，所向披靡啊。不知对于采样定理还灵不灵？嘿，你别说，只要仔细、灵活地分析，一样能制服采样定理。具体分析推导见附录C，请有兴趣的同学立即跳转。