奈奎斯特稳定性判据的数学基础

建立在复变函数理论基础上的幅角原理是奈氏判据的数学基础，首先将幅角原理作一简要介绍。

（1）映射的概念

若F（s）为单值，在S平面上，除有限个奇点外，处处解析，则对于S平面上的每一个解析点，在F平面上，必有一点F（s）与之对应。如F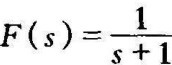，在S平面上，取s＝1，则在F（s）平面上，有，在S平面上，取s＝﹣1＋j，则在F（s）平面上，有F（s）＝﹣j1。若在S平面上，任取一封闭轨迹Гs，且使Гs不通过F（s）的奇点，则在F平面上，就有一封闭轨迹ΓF与之对应。

（2）幅角原理

设F（s）除S平面上的有限个奇点外，为单值连续正则函数，若在S平面上任选一条封闭曲线Гs，并使Гs不通过F（s）的奇点，则在S平面上的封闭曲线Гs映射到F（s）平面上也是一条封闭的曲线ΓF。当解析点s按顺时针方向沿Гs变化一周时，则在F（s）平面上，ΓF曲线按逆时针方向绕原点的圈数N为封闭曲线Гs内包含的F（s）的极点数P与零点数Z之差，即

N＝P－Z

式中，若N＞0，表明ГF逆时针包围F（s）平面上的原点N周；若N＜0，表明ΓF顺时针包围F（s）平面上的原点N周；若N＝0，则说明ΓF曲线不包围F（s）平面上的原点。

由幅角原理，可以确定函数F（s）被曲线Гs所包围的极点与零点的个数之差。封闭曲线Гs和ΓF的形状不影响上述结论。

关于幅角定理的数学证明请读者参考有关书籍，这里仅从几何图形上加以简单说明。(www.xing528.com)

设有辅助函数为

其零、极点在S平面上的分布如图5-34所示，在s平面上作一封闭曲线Γs，且Γs不通过上述零、极点，在封闭曲线Γs上任取一点s1，其对应的辅助函数F（s1）的幅角应为

图5-34 S平面与F（s）平面的映射关系

当解析点s1沿封闭曲线Гs按顺时针方向旋转一周后再回到起始点时，由图可知，所有位于封闭曲线Γs外面的辅助函数F（s）的零、极点指向s1的向量转过的角度都为零，而位于封闭曲线Γs内的F（s）的零、极点指向s1的向量都按顺时针方向转过2πrad（一周）。这样，对图5-34（a），Z＝1，P＝0，∠F（s1）＝﹣2π，即N＝﹣1，F（s1）绕F（s）平面原点顺时针一周；对图5-34（b），Z＝0，P＝1，∠F（s1）＝2π，即N＝1，F（s1）绕F（s）平面原点逆时针旋转一周；对图5-34（c），Z＝1，P＝1，∠F（s1）＝0，即N＝0，F（s1）不包围F（s）平面的原点。

将上述分析推广到一般情况则有

∠F（s）＝2π（P－Z）＝2πN

由此得到幅角原理的表达式为

N＝P－Z（5-59）