奈奎斯特稳定性判据及其应用

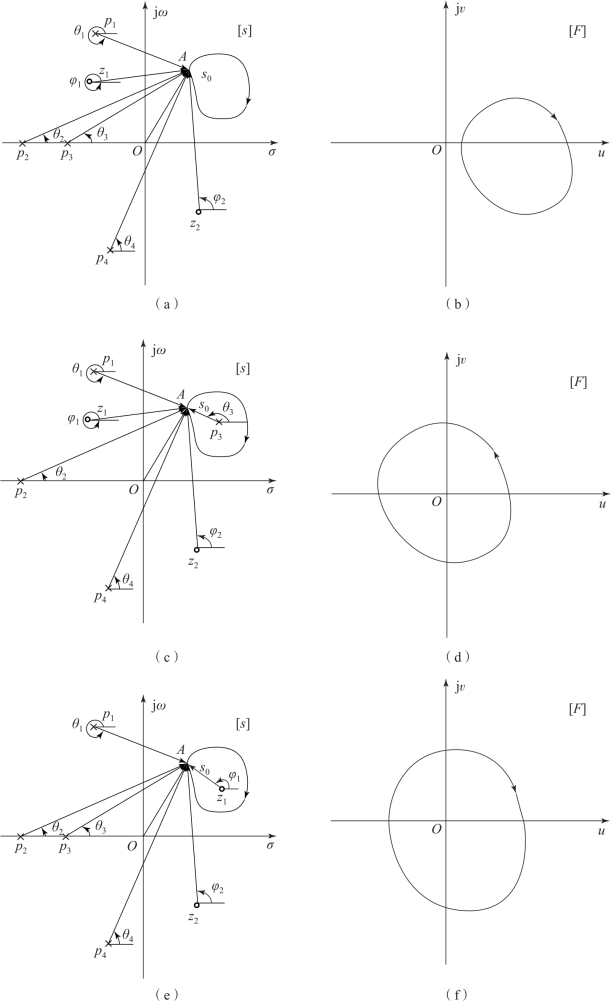
图6－33　s 平面和F（s） 平面的映射关系

图6－34　奈奎斯特路径

原则上， 将奈氏路径确定后， 就可通过令s 沿奈氏路径顺时针转动一周取值， 绘制F（s）的轨迹， 根据F（s） 绕原点的周数N 以及开环传递函数的极点数P 求出Z 来判别闭环系统的稳定性。

奈氏路径Γs 可分为如下三个部分。

（3） 当F（s） 在虚轴上有极点时， 设其为p1。 s 沿以极点p1 为圆心、 以ε→0 为半径的半圆变化， 即s ＝εejθ（ε→0）， θ 从－90°→0°→90°变化。 由于θ 从－90°→0°→90°变化， 所以有

由于小圆半径ε→0， 故认为对于j≠1 有

由式（6.69） 可知， Δ∠F（s） ＝－180°。

综合以上分析可知， 只有s 沿Γs 的第一部分和第三部分变化时， F（s） 的幅角才能产生变化。

1. F（s） 在虚轴上没有极点的情况

由G（jω）H（jω） ＝F（jω）－1 可知， 在复平面内将F（jω）向左移动一个单位即可得到G（jω）H（jω）。 F（jω）与G（jω）H（jω）的关系如图6－35 所示。 从图中可以看出， F（jω）包围原点的圈数等于G（jω）H（jω）包围（－1， j0） 点的圈数。 这样就可以通过绘制G（jω）H（jω）曲线， 即开环幅相频率特性曲线判别闭环系统的稳定性。

图6－35　F（jω）与G（jω）H（jω）的关系

(www.xing528.com)

2. F（s）在原点处有极点的情况

开环系统在虚轴上有极点的情况在本节中只讨论极点位于原点， 即含有积分环节。 除在ω ＝0 rad／s 附近外， s 在s 平面的其他位置上移动与虚轴上无极点时相同。

若极点位于原点处， s 在沿以原点为圆心， 以ε→0 为半径的半圆移动时， 由于小圆半径ε→0， 所以有

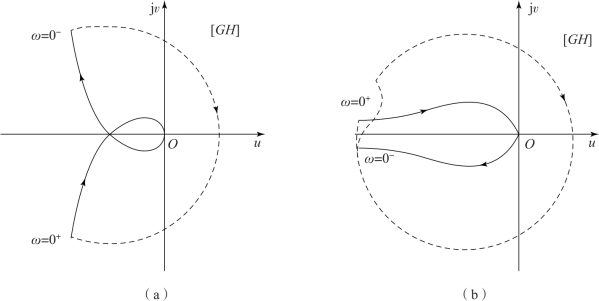
图6－36　开环系统有积分环节时的幅相频率特性曲线

由式（6.72） 可以看出， 只要知道开环传递函数， 就可以判断开环传递函数G（s）H（s）在s 平面右半部的极点数， 并绘制开环系统幅相频率特性曲线，观察其包围（－1， j0） 点的圈数， 得到闭环传递函数在s 平面右半部的极点数， 进而判断闭环系统的稳定性。 因此， 判断幅相频率特性曲线包围（－1， j0）点的圈数十分重要。 对于简单的曲线， 可以直接判断， 但对于图6－37 所示的曲线， 需要借助穿越的概念进行判断。

穿越是指开环系统幅相频率特性G（jω）H（jω）曲线通过（－1， j0） 点以左的负实轴。 沿ω 增加的方向， G（jω）H（jω）自上而下地通过（－1， j0） 点以左的负实轴称为正穿越， 它意味着ω 增加时幅相频率特性的幅角增加； 反之， 则为负穿越。开环系统幅相频率特性G（jω）H（jω）曲线自上而下止于或自上而下起于（－1， j0） 点以左的负实轴， 称为半次正穿越； 反之， 若G（jω）H（jω）曲线自下而上止于或自下而上起于（－1， j0） 点以左的负实轴， 称为半次负穿越。

正穿越一次对应G（jω）H（jω）曲线逆时针包围（－1， j0） 点一周， 负穿越一次对应G（jω）H（jω）曲线顺时针包围（－1， j0） 点一周。 因此， 开环系统幅相频率特性曲线包围（－1， j0） 点的圈数可表示为

对于图6－37 所示的开环系统幅相频率特性曲线， 正穿越两次， 负穿越一次， 因此N ＝1。

【例6－7】　若系统开环传递函数为

图6－37　某系统的幅相频率特性曲线

试用奈奎斯特稳定性判据判断其闭环系统的稳定性。

解： 由于开环系统在右半平面没有极点， 故P ＝0。 由传递函数可知， 有一个积分环节， 因此要逆时针补画90°的圆弧， 开环系统幅相频率特性曲线如图6－38 所示。

从图中可以看出， 开环系统幅相频率特性曲线顺时针包围（－1， j0） 点一圈， 即N ＝－1， 根据奈奎斯特稳定性判据有

所以系统不稳定， 且在右半复平面有2 个闭环极点。