机械杠杆机构的形式与特性

机械杠杆机构有简单式和复合式之分。简单式可分为对应式和非对应式，复合式可分为串联复合式和并联复合式。复合式杠杆放大机构由两个或两个以上简单式杠杆机构组成，目的是得到较大的放大倍数。

（1）简单对应杠杆式

简单对应杠杆式放大机构有如图5-4所示的三种基本形式。

1）图5-4a所示是“正切-正切”型杠杆放大机构。其特点是：杠杆的两臂长度随测杆的移动量y的变化而改变；短臂与测杆的接触点和长臂的放大端点均作直线运动，但它们在通过杠杆铰支点的水平直线上的投影对该支点的距离l₁和l₂固定不变。

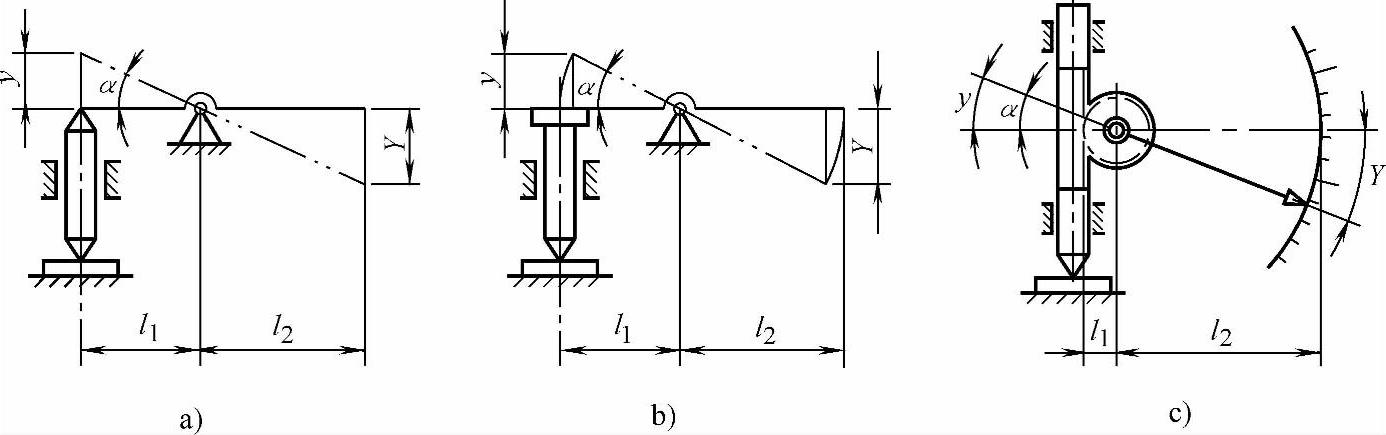
图5-4 简单对应杠杆式放大机构的形式

a）“正切-正切”型 b）“正弦-正弦”型 c）“圆弧-圆弧”型

当测杆直线移动y时，杠杆的偏转规律为

tanα=y／l₁

于是位移放大量Y为 Y=l₂tanα=yl₂／l₁

2）图5-4b所示是“正弦-正弦”型杠杆放大机构。其特点是：杠杆的两臂长度不变；两臂的端点作圆弧运动，它们在水平直线上的投影对支点的距离随之改变。

当测杆直线移动y时，杠杆的偏转规律为

sinα=y／l₁

显然，位移放大量Y为Y=l₂sinα=yl₂／l₁

因为测杆移动量y和放大量Y是杠杆绕其支点偏转α角时所对应的弦长，所以叫作“正弦-正弦”型放大机构。

3）图5-4c所示是“圆弧-圆弧”型杠杆放大机构。测杆上部有齿条与齿轮啮合，齿轮与指针连成一体起杠杆作用。其特点是：杠杆的两臂长度不变，测杆移动量y与齿轮偏转角α所对应节圆的圆弧长相等。y对应的放大量Y亦用圆弧长来表示，故称“圆弧-圆弧”型。

测杆移动量y与齿轮的转角α的关系为

α=y／l₁

显然，位移放大量Y为Y=l₂α=yl₂／l₁

机构的输出放大量Y与其输入移动量y之比叫作该机构的放大倍数，以M表示。上述三种对应式杠杆机构的放大倍数均为

M=Y／y=l₂／l₁

可见，这种对应杠杆式放大机构的放大倍数是杠杆长短臂之比，是一个常数。

图5-4所示三种对应式杠杆放大机构的形式及其放大倍数变化率_η见表5-1。可见，这种对应式放大机构的放大倍数变化率为1，这也表明放大倍数M是常数。

（2）简单非对应杠杆式

非对应杠杆式放大机构有六种：“正切-正弦”型、“正切-圆弧”型、“正弦-正切”型、“正弦-圆弧”型、“圆弧-正切”型和“圆弧-正弦”型（见表5-2）。

表5-1 简单对应杠杆式放大机构的形式及其放大信数变化率η

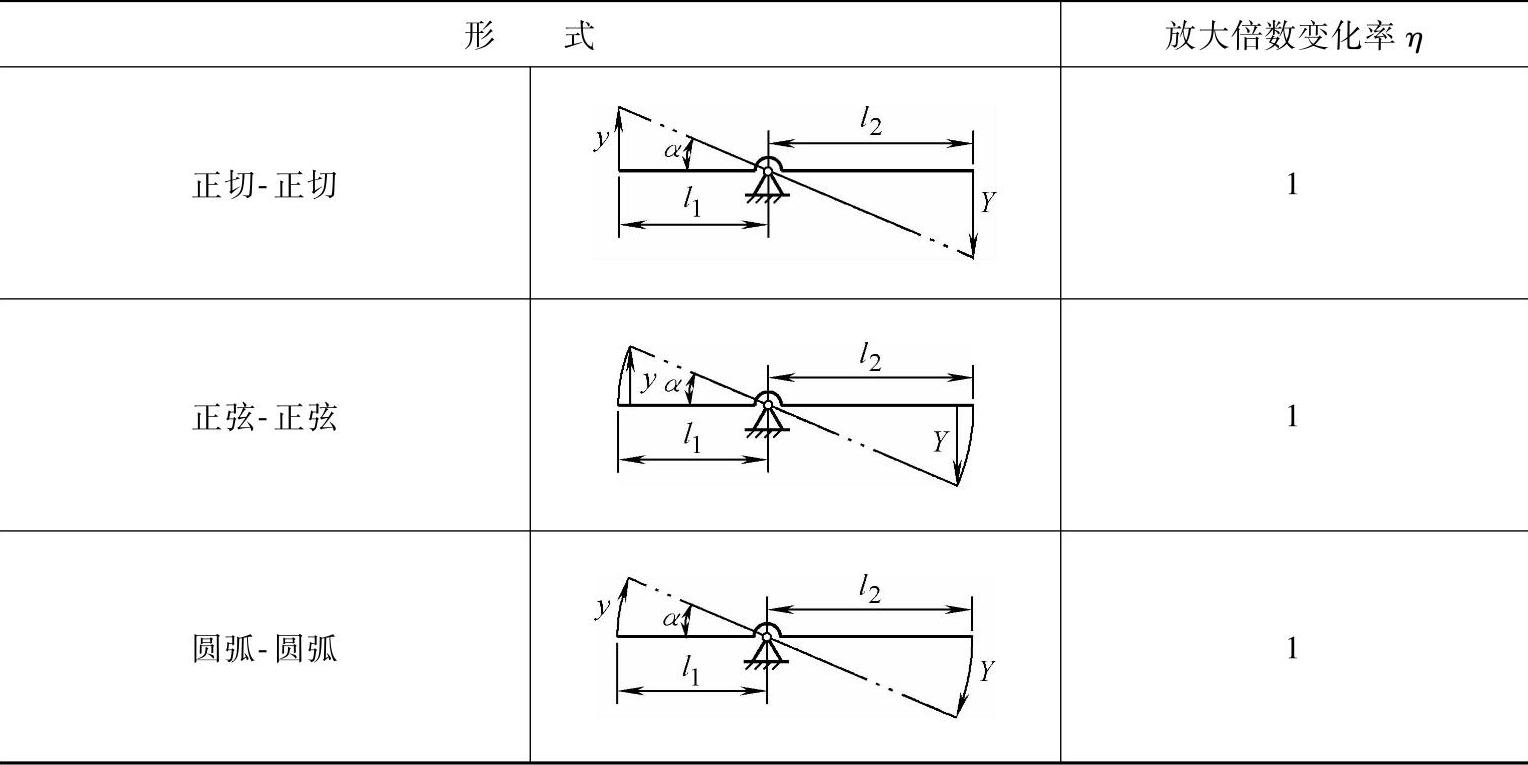
表5-2 简单非对应杠杆式放大机构的形式及其放大信数变化率η

对于非对应式杠杆机构的放大倍数，须结合杠杆不同运动形式进行分析。现以表5-2中的“正切-正弦”型和“正切-圆弧”型为例计算如下。

1）“正切-正弦”型，意为以正切式移动作输入量，以正弦式移动为放大量。由上述对应式可知，正切式移动量为

y=l₁tanα

在任一瞬间，其移动变量dy与相应的角变量dα的关系是取上式的导数，即

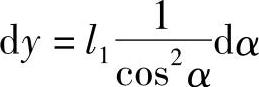
对于以正弦式作放大量的关系式，则为

Y=l₂sinα

取导数为dY=l₂cosαdα

设以M′表示非对应式杠杆放大机构的放大倍数，根据放大倍数的定义，则上例的放大倍数为

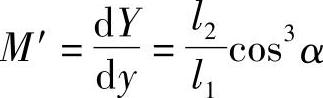
因所有对应式杠杆机构的放大倍数M均为l₂／l₁，所以上式可写为

M′=Mcos³α

2）“正切-圆弧”型，意为以正切式移动作输入量，以圆弧式移动为放大量。由上述已知正切式移动变量dy，即

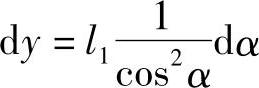
又因为圆弧式移动放大量为Y=l₂α，取导数为

dY=l₂dα

同理，可求得其放大倍数为

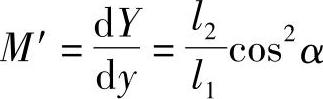
M′=Mcos²α

可见，非对应杠杆式放大机构的放大倍数是随杠杆偏转角度的不同而变化的。非对应式放大倍数M′与对应式放大倍数M之比称为放大倍数的变化率，以η表示，即

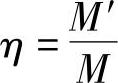
于是，上两例的放大倍数的变化率分别为：

对于“正切-正弦”型η=cos³α

对于“正切-圆弧”型η=cos²α

同理，可求出其余四种非对应杠杆式的放大倍数变化率。现将非对应杠杆式的放大机构的形式及其放大倍数变化率η列于表5-2。

由表5-1和表5-2可知：

1）当η=1时，表示放大倍数M是常数，不随y的变化而变化。

2）当η＞1时，表示放大倍数是变量，它随y值的增大而递增。

3）当η＜1时，表示放大倍数是变量，它随y值的增大而递减。

由此可见：

1）只有η=1的放大机构，才能使y与Y之间具有线性放大的传递关系。因此，对于要求有均匀刻度、放大倍数为常数的杠杆机构，宜采用对应式杠杆机构。

2）对于η＞1或η＜1的非对应式放大机构，η是y／l₁的函数。为使η尽量接近于1，应使比值y／l₁尽量小。当测杆的最大位移量y一定时，尽可能增大杆臂l₁的长度，可使y／l₁减小，但在要求有一定的放大倍数M的情况下，则要相应地增长杆臂l₂的长度。然而l₂直接影响结构尺寸的大小，所以设计时须考虑结构的可能性。一般对于指针式的放大机构，l₂长度一般不超过150mm。简单杠杆式放大机构的放大倍数有一定的限制，不可能太大。例如要求放大倍数为150，取l₂=150mm，则需有l₁=1mm，这样的机构是难以实现的。若要获得较大的倍数，需采用复合式杠杆机构。

（3）串联复合杠杆式(www.xing528.com)

串联复合杠杆式放大机构是指多个简单杠杆式放大机构依次传递运动的杠杆机构。

利用表5-1和表5-2的各种简单对应式或非对应式杠杆放大机构，按不同组合便可构成多种复合杠杆式放大机构。例如，利用表5-1的“正切-正切”型可分别与正切、正弦和圆弧放大型组成三种复合式，即“正切-正切→正切”型、“正切-正切→正弦”型和“正切-正切→圆弧”型。同时，还可以构成相反的形式，即“正切→正切-正切”型、“正弦→正切-正切”型和“圆弧→正切-正切”型。其余类推。

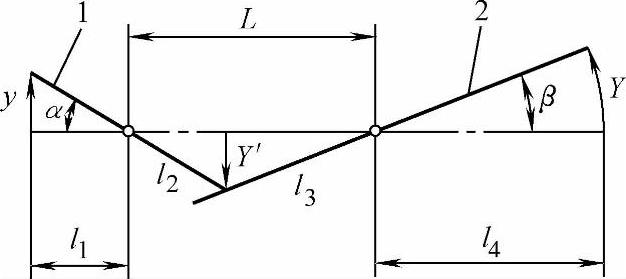
图5-5 “正切-正弦→圆弧”型串联复合杠杆式放大机构

图5-5所示是利用“正切-正弦”型和圆弧放大型组成的“正切-正弦→圆弧”型复合杠杆式放大机构。图中杠杆1的长臂l₂的端点与杠杆2的短臂l₃直接接触。l₃是变值，L是两杠杆铰支点间的距离。当测杆直线移动y时，首先通过杠杆1作正弦型放大为Y′，然后用杠杆2作圆弧型放大为Y。机构的放大倍数计算如下。

由图5-5所示几何关系有

tanα=y／l₁

α=arctan（y／l₁）

Y′=l₂sinα

而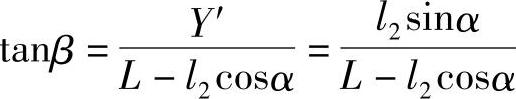

所以

又 Y=l₄β

故放大倍数为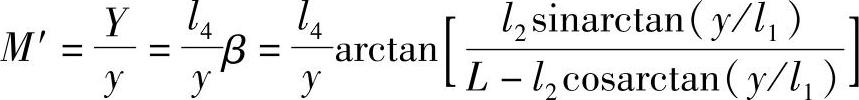

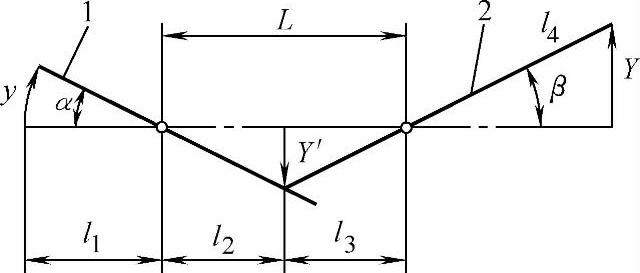
图5-6 “圆弧→正切-正弦”型串联复合杠杆式放大机构的形式

图5-6所示的“圆弧→正切-正弦”型机构是上述机构的相反组合型。这时，被测值y按圆弧变动，通过杠杆1作正切式的中间放大，其放大量为Y′，然后用杠杆2作正弦型放大为Y。机构的放大倍数计算如下：

由几何关系有

α=y／l₁

Y′=（L-l₃）tanα

而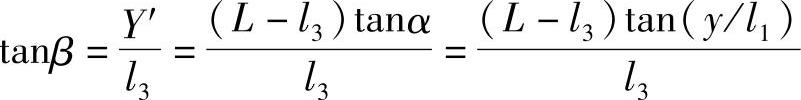

所以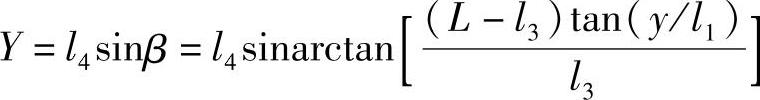

故放大倍数为

可见，以上两例的放大倍数不是常数，而是随y的变化而改变的量，即机构存在η≠1的放大倍数变化率。

经计算分析表明，串联复合杠杆放大机构只有按表5-3所列的组合形式才能实现放大倍数为常数，即η=1。对于不符合表5-3所列的组合关系和条件的任何串联复合式，其放大倍数均不为常数，即η＞1或η＜1。

表5-3 η=1的串联复合杠杆式放大机构

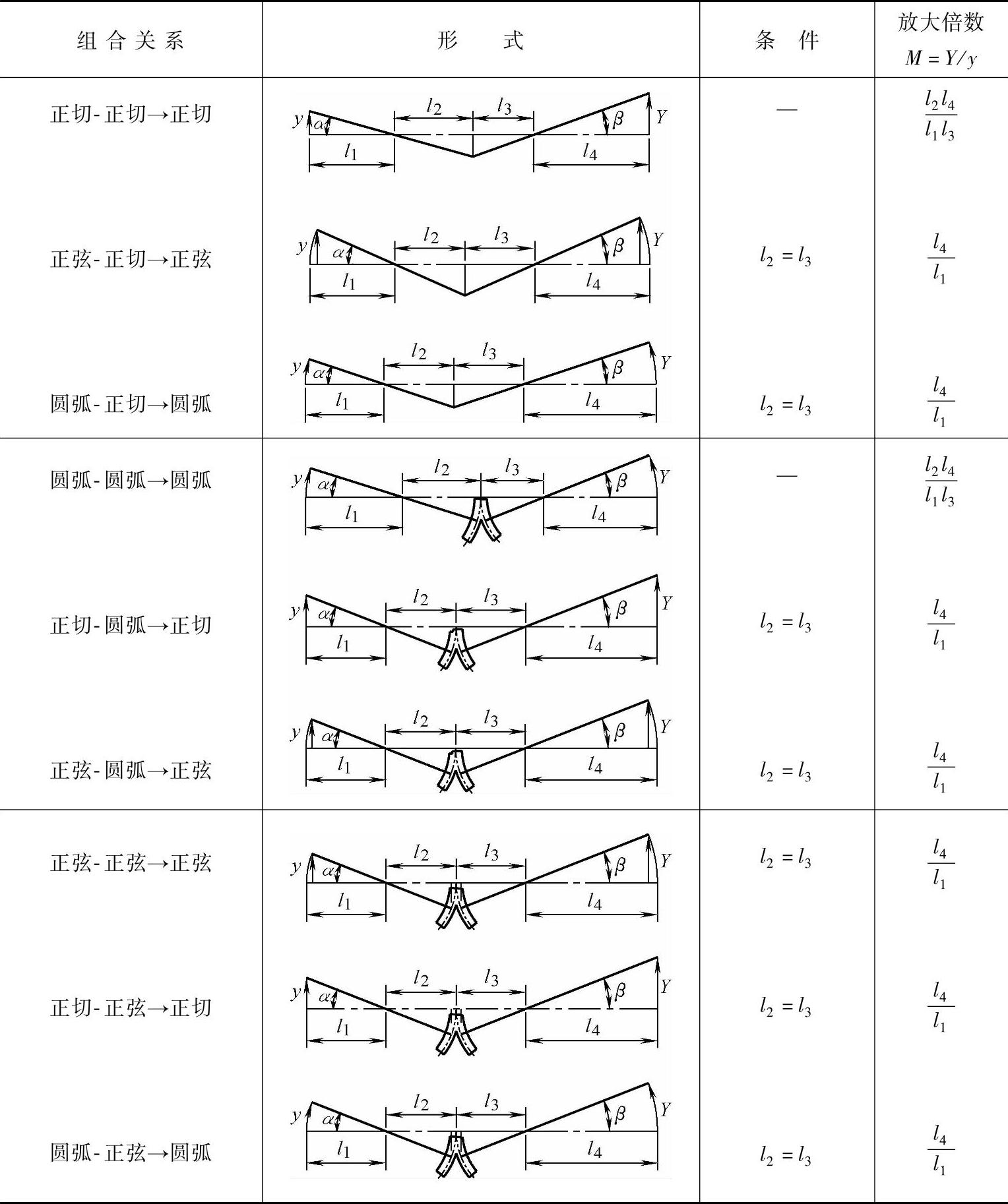
从表5-3可知，对η=1的组合放大机构，其输入量y和放大量Y必是同一运动形式，如正切式输入必为正切式放大，正弦式输入必为正弦式放大等。其次，表中除“正切-正切→正切”型和“圆弧-圆弧→圆弧”型两种复合式外，其他各种复合式机构要实现M为常数，必定要满足l₂=l₃的条件。

（4）并联复合杠杆式

并联复合杠杆式放大机构是指每两个简单杠杆式机构之间是通过中间传动件来传递运动的杠杆机构。

从图5-5和图5-6所示的两例可知，用不同对应式的两杠杆组成的串联复合放大机构，其放大倍数是变量。其原因是输入值y和放大量Y的变化规律不同；其次是两杠杆的串联接触点在传递运动过程中发生移动，使l₂和l₃的长度产生不同的变化，改变了杠杆原来对应式传动的性质。如果采用并联复合式杠杆机构，在两杠杆接触点处装入一个中间传动杆，则可使放大倍数为常量，即η=1。

图5-7所示是由“正弦-正弦”型杠杆1和“正切-正切”型杠杆2按平行排列构成的并联复合杠杆式放大机构，两杠杆之间装入中间传动杆3，它既起到两杠杆的传动作用，又改善了机构的特性。

杠杆1的长臂l₂的尖端与中间传动杆3的平端接触，以实现正弦型放大；杠杆2的短臂l₃平端与中间传动杆3的尖端接触，以实现正切型放大。可见，中间传动杆3的作用就是将杠杆1的正弦型放大转换为杠杆2的正切型放大，实际上它是一种转换元件。通过它的中间转换，使两杠杆保持它们原来的对应式，从而实现η=1的、放大倍数不发生变化的传动。

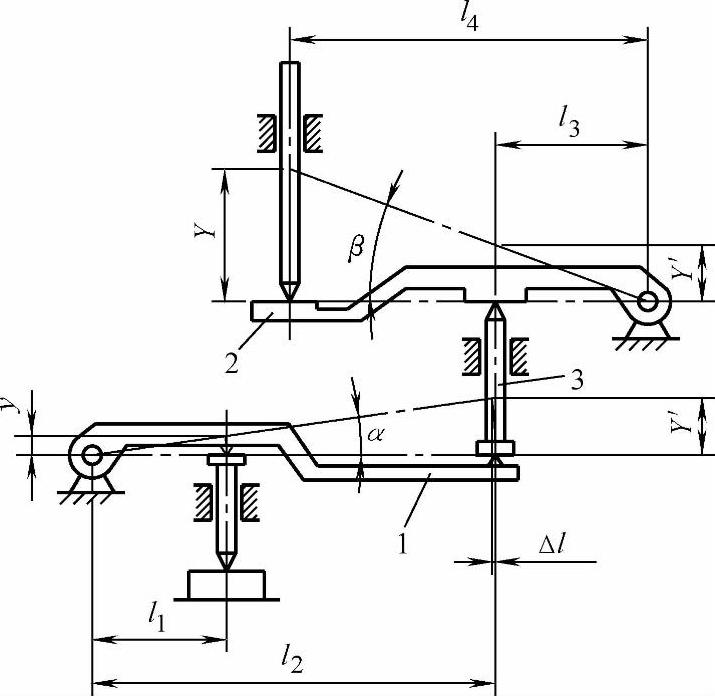
图5-7 “正弦-正弦”型和“正切-正切”型并联复合杠杆式放大机构

1、2—杠杆 3—中间传动杆

由图5-7所示的几何关系不难得出该机构的放大倍数为

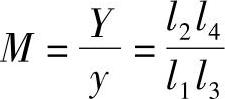
假定没有中间传动杆3，让杠杆1的长臂l₂的端点直接与杠杆2的短臂l₃的平端接触，那么，当长臂l₂的端点位移为Y′时，接触点便会向左边移动一个距离Δl，这也就是使l₃增长了的量，因而引起放大倍数的变化。

图5-8所示是由两个非对应式杠杆组成的并联复合杠杆式放大机构。杠杆1是“正切-正弦”型，η₁＜1；杠杆2是“正弦-圆弧”型，η₂＞1。中间传动杆3的作用是使两杠杆原有的放大倍数变化率保持不变。

此机构的总放大倍数变化率为

η=η₁η₂

由表5-2可知，对于“正切-正弦”型有η₁=cos³α；对于“正弦-圆弧”型有η₂=1／cosβ。于是

η=cos³α／cosβ

这表明，机构的放大倍数不是常数，而是随α、β角的变化而变化的。但是，这种并联复合式机构在一定条件下可实现放大倍数很接近常量。这时，令η=1，即cos³α=cosβ或cos⁶α=cos²β。因为l₂的尖端和l₃的尖端均作同量的“正弦”变化，所以有

l₂sinα=l₃sinβ

或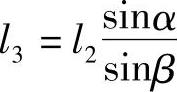

由三角函数关系有

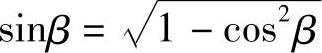
按η=1的要求有

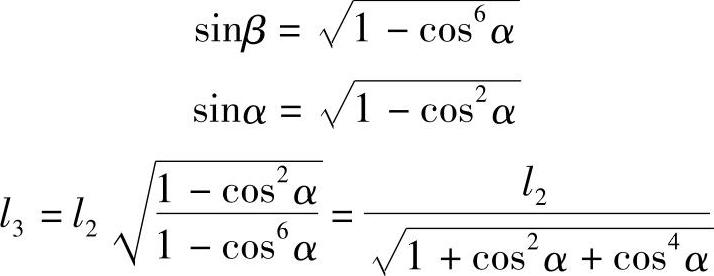
当α很小时有

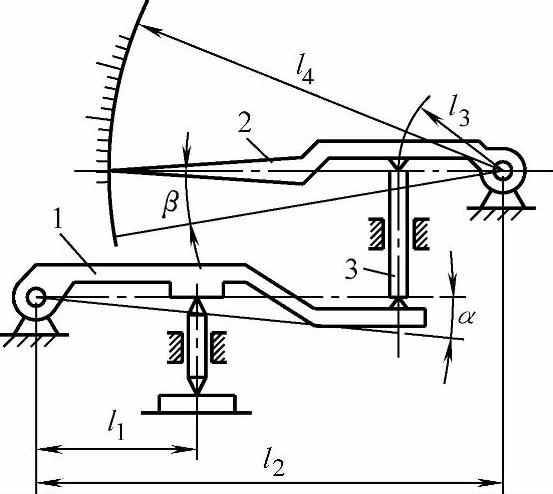
图5-8 “正切-正弦”型和“正弦-圆弧”型并联复合杠杆式放大机构

1、2—杠杆 3—中间传动杆

上式表明，只要机构满足此条件，则可得η≈1，机构的放大倍数近似于常量。

图5-9所示是由“正弦-正弦”型和“正切-正切”型互成直角组成的串联复合杠杆式放大机构。这种机构虽是串联式，又无中间传动杆作转换元件，但可实现η=1的放大。其原理分析如下。

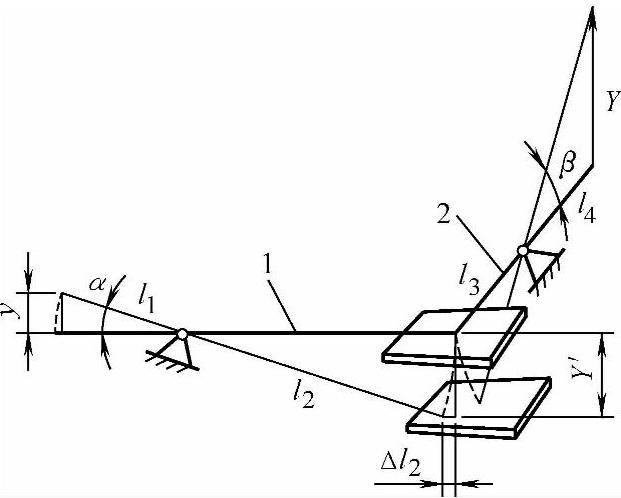
图5-9 “正弦-正弦”型和“正切-正切”型互成直角的串联复合杠杆式放大机构

杠杆1的旋转面与杠杆2的旋转面互相垂直。杆臂l₂的端点与杆臂l₃的端面相接触。当杠杆1旋转一个角度α时，l₂的端点与l₃端面的接触点虽然移动了一个距离Δl₂，但这个量不是产生在杠杆2的长度方向，所以不影响杆臂l₃的长度变化。因此，杠杆2的转角β仅取决于杠杆1转动时长臂l₂按正弦变化所确定的移动量Y′。而这个Y′又是杠杆2的短臂l₃按正切变化的移动量，最后又以正切型放大为Y。所以，此机构的放大倍数为常量，即η=1。