PMS马尔科夫建模方法优化

马尔科夫建模方法的基本思想就是将PMS系统用马尔科夫状态转移链表示。每个阶段用一个马尔科夫链表示，每个阶段的状态数取决于该状态的配置情况。把阶段间的转移也看作如同故障和修复似的状态转移，把每个阶段看成是马尔科夫链中的状态^[10]。第i个阶段的输出是第i+1个阶段的输入，最后一个阶段的输出是整个系统的输出。以下使用一个例子^[1]来说明该建模方法的过程和计算方法，此方法能推广应用于更一般的PHM系统。

考虑一个具有三个阶段的任务系统在各个阶段的配置、停留时间、可信性指标情况，见表8-1。

表8-1 三个阶段的任务系统配置、停留时间、可信性指标

（续）

对系统作如下假设：

假设1：系统各个部件存在两种状态：正常和非正常，在状态描述中用1和0表示。

假设2：部件的寿命分布和维修时间分布服从指数分布。

假设3：前一阶段的系统状态只有在满足下一阶段工作状态时才发生阶段的转移。

假设4：PMS进入阶段i之后的行为与其进入阶段i之前的行为无关，且与何时进入阶段i无关。

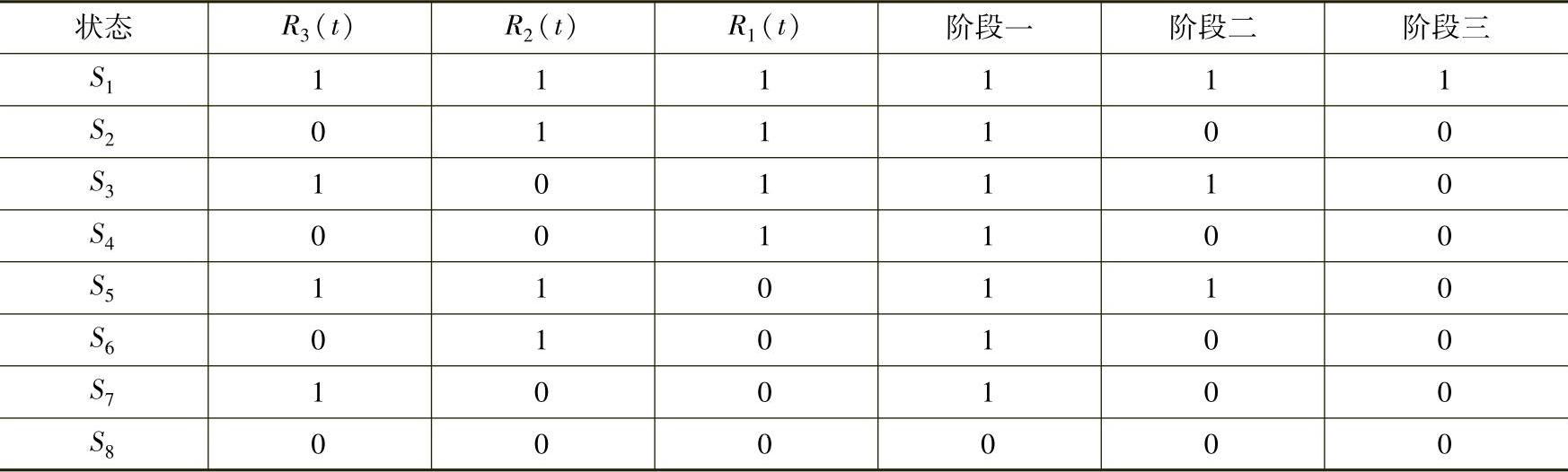
表8-2描述了各个阶段中状态及对应的系统情况。表8-1还包含了各个阶段内系统是否处于正常工作的信息，它说明了转入某个阶段时前一阶段的各个部需处于的状态。例如阶段一中，系统如果处于S₈状态，则意味着系统失效，而其他状态则意味着系统正常工作，其中S₁、S₃、S₅也是阶段二的工作状态，所以在阶段转移发生时，系统各部件配置必须处于这三个状态，系统才能转移到阶段二。

表8-2 各个阶段中状态及对应的系统

由假设2，设三个部件的故障率和维修率分别为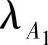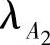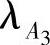，，和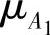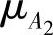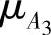，，，则根据齐次马尔科夫的理论可以得到阶段一时系统的状态转移速率矩阵如下：

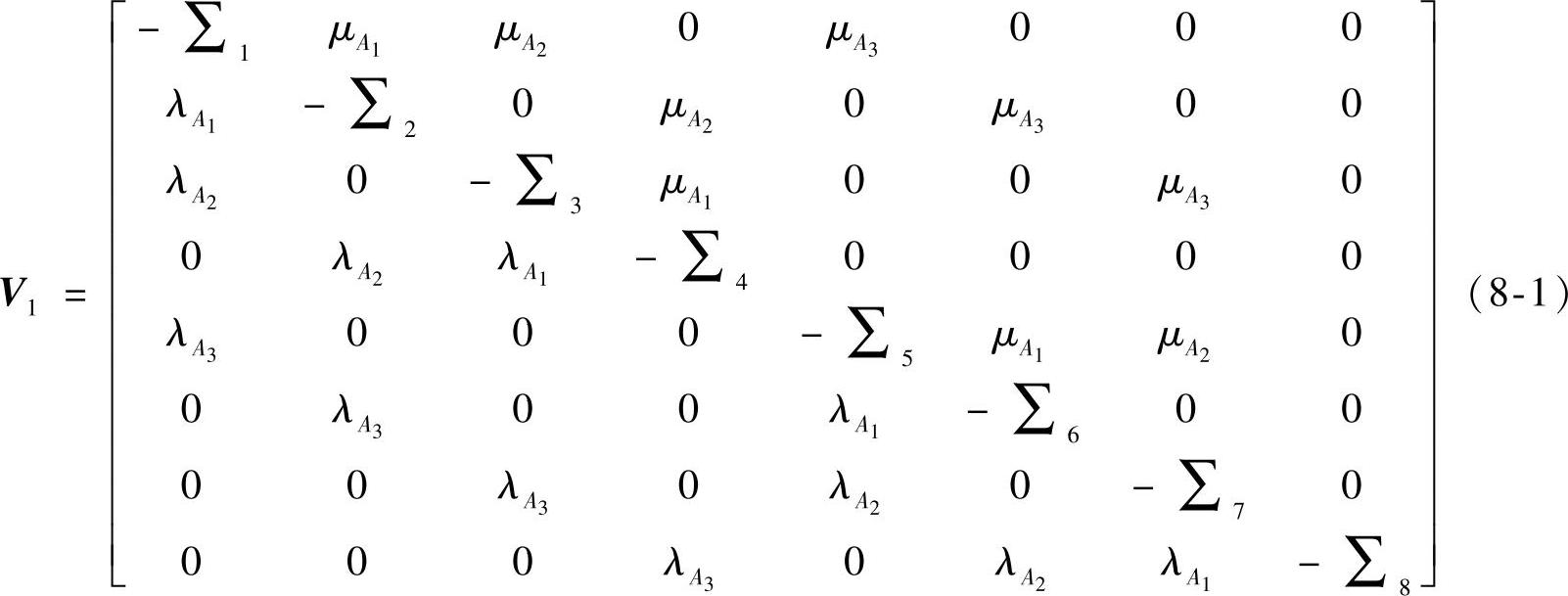
式中，∑_i为第i行的和。

结合状态方程P′（t）=V₁P（t），令初始状态P_i1（0）=[1，0，0，0，0，0，0，0]^T可以计算出阶段一结束时，系统的可靠并能成功转移到阶段二的概率为

R（t₁）=P₁（t₁）+P₃（t₁）+P₅（t₁） （8-2）

由S₁、S₃、S₅这三个状态进入阶段二后，为了使任务完成并成功进入阶段三，系统在阶段二完成时状态须停留在S₁，因为S₁是阶段二和阶段三共有的系统正常工作的状态。同样阶段二中系统状态发生齐次马尔科夫状态转移。其状态转移速率矩阵为(www.xing528.com)

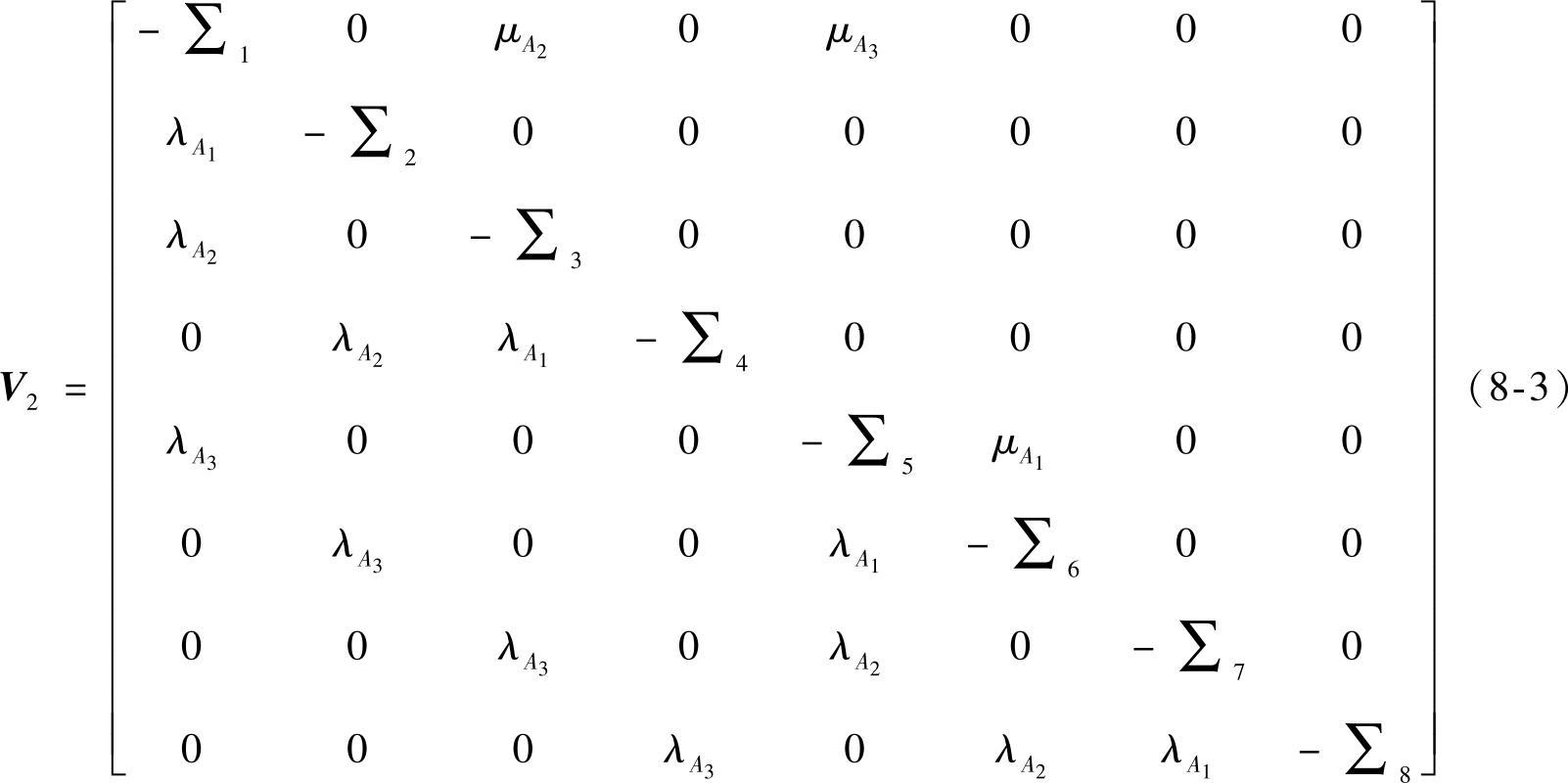
式中，∑_i为第i行的和。

状态方程为P′（t）=V₂P（t）。此时的初始状态需要考虑阶段一结束时的状态概率。由于进出阶段二时系统可能处于状态S₁、S₃或S₅，其概率分别为P₁（t₁）、P₃（t₁）和P₅（t₁）。所以阶段二状态方程的初始条件是P_i2（t₁）=[P₁（t₁），0，P₃（t₁），0，P₅（t₁），0，0，0]^T。可解得阶段二结束时系统处于状态S₁的概率Q₁（t₂-t₁）。

阶段三中，同理可得该阶段的状态转移速率矩阵为

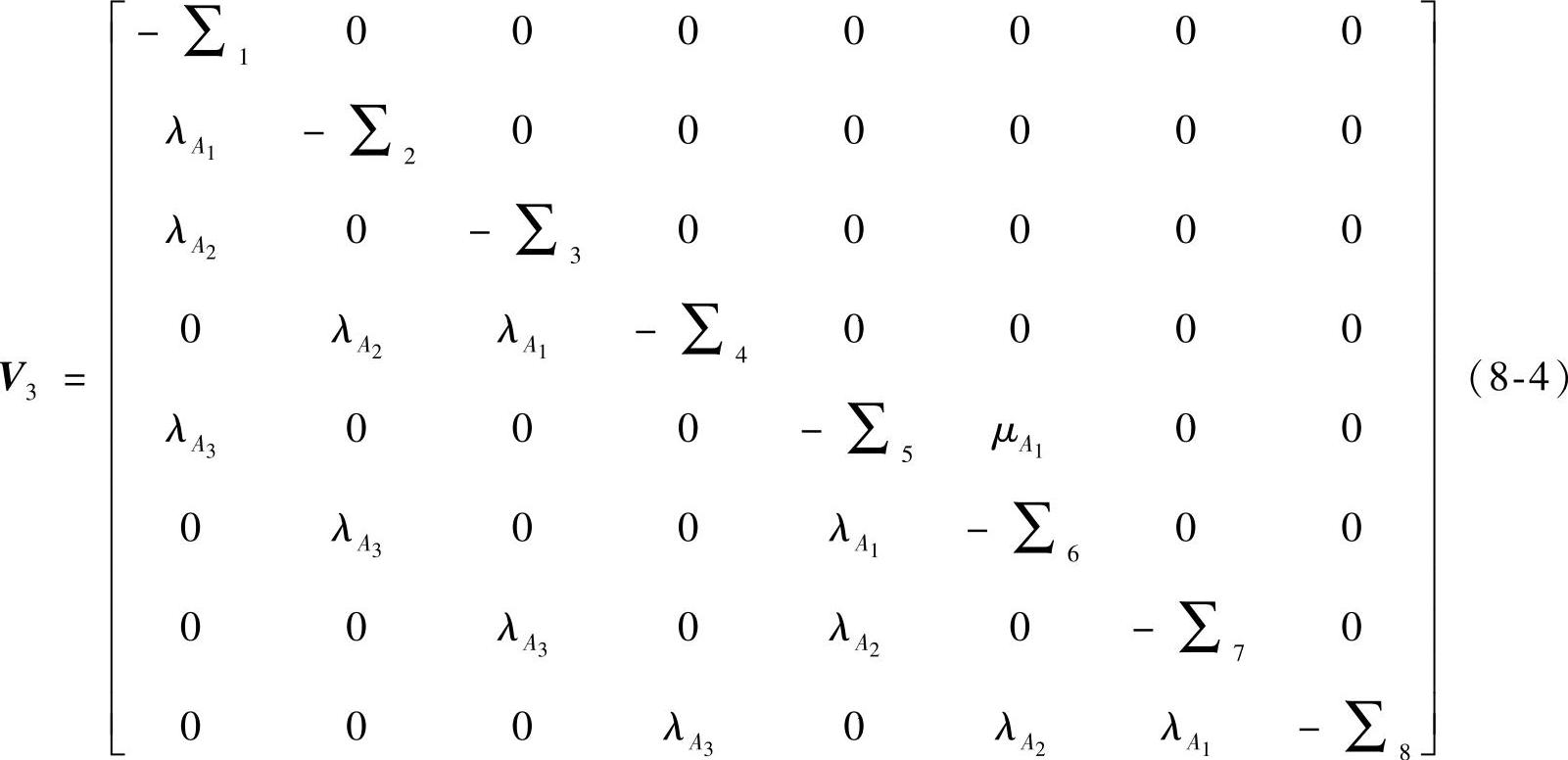
式中，∑_i为第i行的和。

状态方程为P′（t）=V₃P（t）。此时的初始状态为P_i3（t₂）=[Q₁（t₂-t₁），0，0，0，0，0，0，0]^T，故可解得该PMS系统最终任务完成的概率为阶段三最后处于状态S₁的概率：

P{多阶段任务成功}=Z₁（t_f-t₂） （8-5）

上面的多阶段任务模型中假设每个阶段的运行时间是一定的，但在实际过程中，任务的执行往往受到一些随机因素的影响，这使得阶段结束的时间并不是一个确定值而是随机量。描述阶段停留时间随机的PMS系统，一般定义一个阶段转移概率密度函数f（t），表示阶段在时刻t时系统向下一阶段转移的概率。该密度函数是通过对阶段任务特性的分析得到的，通常假设这个概率密度是β分布的。β分布是描述一段时间内的单峰函数，通过参数调节，β分布可呈对称分布、非对称分布、单峰分布、递增或递减分布等，可逼近常见的正态、三角、均匀、反正弦、瑞利等分布。为了方便计算，人们通常用β分布中的一种特例——平均分布来表示^[10]。

阶段的状态概率密度函数曲线如图8-2所示。图8-2中，P_i（t）表示某个阶段中在t时刻处于第i个状态的概率，f（t）为[T_i1，T_i2]时间段上的状态停留概率密度函数。通过求P_i（t）在[T_i1，T_i2]上的数学期望可以得到系统发生阶段转移时处于某个状态的概率从而得到下一个阶段的初始概率：

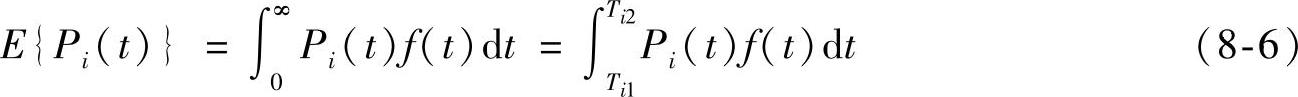
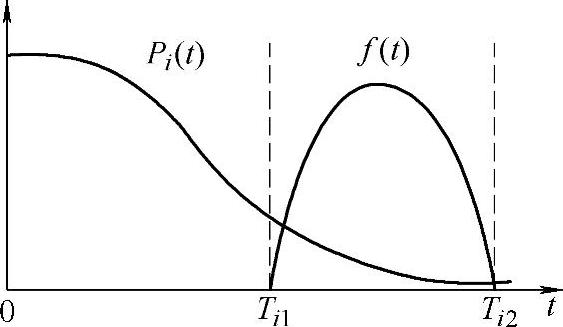
图8-2 阶段的状态概率密度函数曲线

于是上述解法中各阶段的初始概率分别为

P_i1（0）=[1，0，0，0，0，0，0，0]^T （8-7）

P_i2（t₁）={E[P₁（t₁）]，0，E[P₃（t₁）]，0，E[P₅（t₁）]，0，0，0}^T （8-8）

P_i3（t₂）={E[Q₁（t₂-t₁）]，0，0，0，0，0，0，0}^T （8-9）

上述例子中还假设了阶段内状态的转移服从齐次马尔科夫的情况，实际上对于一般系统，状态的停留时间多服从一般分布。对于这种情况，只能用半马尔科夫状态转移的方法解决阶段内的状态概率问题。

考虑到更一般的情况，多阶段任务系统中可能包含更多的部件，某个阶段参与任务的部件不一定在之后或者之前的阶段中出现。随着阶段的增多和部件的增多，整个系统的马尔科夫状态转移链的状态数将呈几何级数增长。一个最基本的简化状态的方法就是只考虑阶段中使用到的部件的状态。