设计速度控制系统的分析介绍

下面以使雷达天线的转速保持一定或按一定规律变化的速度控制为对象，来研究满足前一节给出的性能指标的控制系统。

天线速度控制系统的方框图如图6-50a所示，现将该方框图重新列示为图6-53。

要了解该系统特性，首先研究该系统的根轨迹，确定各种增益系数。若利用计算机，根据图6-53很容易描述根轨迹图。因该系统比较简单，用解析法就可求解特征根，绘制出根轨迹。

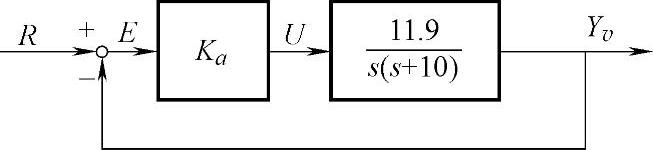
图6-53 转速控制系统的方框图

R—希望速度的基准输入 E—偏差信号（与目标值的偏差） U—对电动机的输入量 Y_v—天线转速的检测信号（输出） K_a—放大器的放大率（增益）

用关键词“特征方程/特征根”原理，该控制系统的特征方程如下：

1+K_aG（s）=0

即，

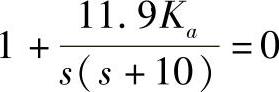
所以，

s²+10s+11.9K_a=0 （6-16）

该特征方程为二次方程，其特征根s₁、s₂可由下式求得

根轨迹图是在使增益系数K_a从0到∞变化时，特征根s₁、s₂在复平面上画出的曲线。所以从上式可简单地求得其根轨迹，见图6-54。二个特征根描叙二条根轨迹。以式（6-17）为例，首先以K_a=0的特征根0、-10为出发点，随着K_a的增加，在负实轴上向-5进展，在K_a=2.1时重根（等根）为-5，共有一点。若K_a再增加，特征根实部成为-5的共轭复数。所以二条根轨迹上下垂直地延伸。K_a→∞时，根轨迹向无限远处（-5，±j∞）延伸。

由图6-54所示的根轨迹可知：

1）因根轨迹都在左半平面，所以该系统对所有的K_a都是稳定的。

2）K_a太小时，特征根在原点附近，这种K_a对控制系统响应的快速性不好，可使滞后时间变大。

3）K_a过大时，特征根实部一定，只是虚部变大，响应出现高频成分，超调量变大。

为搞清楚这些根轨迹的结果，用计算机求输出的时间响应是最直接而可靠的方法。可以用构成数学模型的式（6-8）～式（6-13）或图6-53所示的传递函数和方框图直接进行仿真，只要了解微分方程的数值计算，仿真程序就比较容易编写。

图6-55是在基准阶跃输入r为1V时，用计算机进行仿真所得到的天线速度的检测输出y_v和放大器对DC电动机控制电压u的时间响应仿真结果。1V基准阶跃输入代表天线从停止状态到已设定作为目标的100r/min转速。输出y_v表示每1V为100r/min的信号。(www.xing528.com)

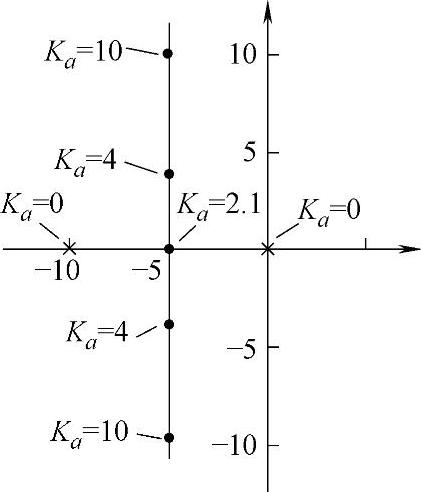
图6-54 天线速度控制系统的根轨迹

图6-55 输出响应和控制力时间历程仿真结果

图6-55给出了放大率K_a分别为1、5、10、20四种情况时的y_v和u的时间历程。首先同图6-54的根轨迹作一比较，发现，放大率在较小的K_a=1时，响应输出y_v缓慢变化，需要很长时间才达到目标值。相反，当K_a为较大的10、20时，响应出现变动成分，超调量过大。这些从上述根轨迹理论中已得到证实。我们再看一下作为DC电动机电压的控制力u的确定，K_a变大，u的振幅也随之变大，能耗也增大。另外，对应所有K_a值的输出，经过一定时间都收敛至1V，所以我们得知这种控制是稳定的而且对阶跃输入的稳态误差为0。通过图6-55可推测出，对应阶跃输入最佳输出响应的K_a值在5左右。

为确认最适当的K_a值，让我们通过仿真来分析一下K_a值在5附近细微变化时的输出响应。图6-56所示为将K_a分别设为3、4、5、6时，输出y_v的响应。由图可见超调量限制在8%以内，使滞后时间较短的K_a值是K_a=4。这时的滞后时间T_d≈0.25s。由此可见，指标3的T_d＜0.75s的条件完全可满足。

综上所述，利用图6-48的结构控制天线的旋转速度，仅将放大器的放大率调节为K_a=4，就可得到满足控制指标1～3的稳定控制系统。

以上是依仿真结果得到该控制系统阶跃输入的稳态误差为0的判断，应用拉普拉斯变换的最终定理，可简单地证明这一点。

可用于稳态误差计算的终值定理：

设时间函数f（t）的拉普拉斯变换为F（s），则：

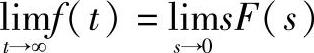
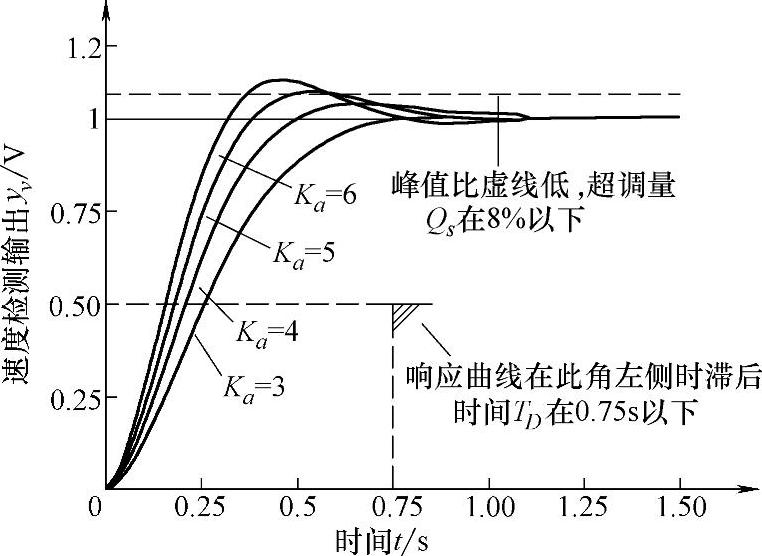
图6-56 控制目标和输出响应

稳态误差E_s是经过一定时间后的偏差信号e=r-y。所以，应用上述终值定理可得：

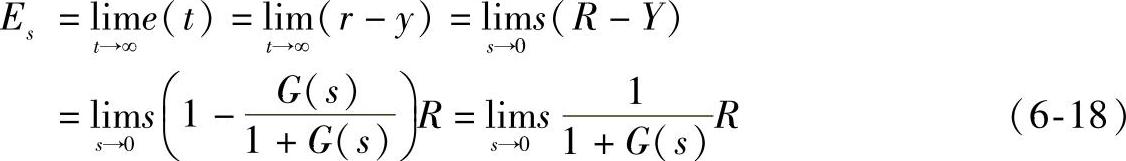
这时，当基准输入r为单位阶跃函数时，R=1/s，而且传递函数G（s）为：

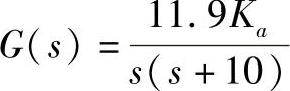
将此式代入式（6-18），求得稳态误差如下：

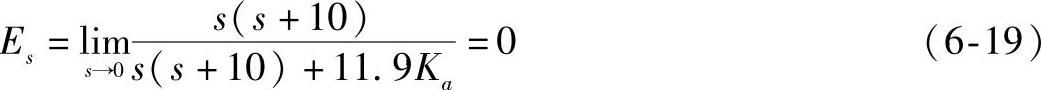
这样，即使不求解时间响应，由控制系统的方框图和传递函数也可直接求得稳态误差E_s。