利用对数频率稳定判据判别闭环系统稳定性

对数频率稳定判据，是奈氏判据的又一种形式，它是将开环极坐标画在对数坐标上，根据开环对数幅频与对数相频曲线的相互关系来判别闭环系统稳定性。由于对数曲线作图方便，所以，对数判据应用较广。

在图5-42上，绘制了一条开环极坐标图及其对应的对数频率特性曲线。

由图5-42可知，极坐标图沿ω增加方向绕（－1，j0）点的圈数N＝0。这一结论也可根据极坐标图在（－1，－∞）的负实轴的穿越次数确定。穿越可定义如下。

正穿越：开环极坐标G（jω）H（jω）曲线，沿ω增加的方向，由上往下穿过（－1，－∞）的负实轴段一次，称为一个正穿越，正穿越数用N＋表示。

半个正穿越：G（jω）H（jω）曲线从（－1，－∞）的负实轴段开始向下，称为半个正穿越。

负穿越：开环极坐标G（jω）H（jω）曲线，沿ω增加的方向，由下往上穿过（－1，－∞）的负实轴段一次，称为一个负穿越，负穿越数用N－表示。

半个负穿越：G（jω）H（jω）曲线，从（－1，－∞）的负实轴段开始向上称为半个负穿越。

图5-42（a）的G（jω）H（jω）曲线对（－1，－∞）的负实轴段的穿越次数为：N＋＝1，N－＝1。则N＝N＋－N－＝1－1＝0，此结果与前述结果一致。所以，奈氏判据也可叙述为：开环极坐标G（jω）H（jω）曲线，沿ω增加的方向，对（－1，－∞）的负实轴段正、负穿越次数之差等于，则闭环系统稳定。P 为开环正极点数，即

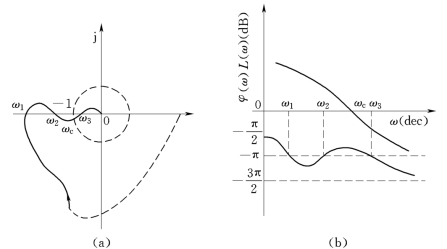
图5-42　极坐标图（a）及对应的对数频率特性曲线（b）

将开环极坐标曲线与对数频率特性曲线对照，可引出对数频率判据。

G（jω）H（jω）曲线对（－1，－∞）的负实轴段上的正、负穿越，对应开环对数幅频曲线L（ω）＞0dB的频率范围内，相应对数相频曲线对－π线的正、负穿越，不过这时正、负穿越的含义是：

正穿越：在L（ω）＞0dB的频率范围内，其相频曲线由下往上穿过－π线一次，称为一个正穿越，正穿越数用N＋表示。从－π线开始往上称为半个正穿越。

负穿越：在L（ω）＞0dB的频率范围内，其相频曲线由上往下穿过－π线一次，称为一个负穿越，负穿越数用N－表示。从－π线开始往下称为半个负穿越。

当开环传递函数含有积分环节时，对应在对数相频曲线上ω为0＋处，用虚线向上补画角。在计算正、负穿越时，应将补上的虚线看成对数相频曲线的一部分。

对数频率稳定判据可叙述如下：

闭环系统稳定的条件是：在开环对数幅频L（ω）＞0dB的频率范围内，对应的开环对数相频曲线φ（ω）对－π线的正、负穿越之差等于，即

式中 P——开环正极点的个数。

图5-42（b）的对数频率特性曲线，在L（ω）＞0dB 的频率范围内，对应相频φ（ω）曲线对－π线的N＋＝1，N－＝1。则N＝N＋－N－＝1－1＝0。此结果与前面计算的结果一致。

【例5-9】 已知系统开环传递函数

试用对数稳定判据判别闭环稳定性。

解：绘制系统开环对数频率特性如图5-43所示。开环有一个积分环节，需在相频曲线ω＝0＋处向上补画π/2 角。由开环传递函数可知P＝0。

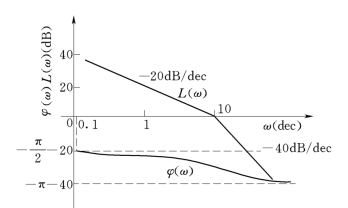
图5-43　例5-9 系统开环对数频率特性曲线

由图可知，在L（ω）＞0dB 的范围内。对应相频曲线对－π线没有穿越，即N＋＝0，N－＝0，则

所以闭环稳定。

【例5-10】 已知系统开环传递函数

试用对数稳定判据判别闭环稳定性。

解：绘制系统开环对数频率特性如图5-44所示。开环有一个积分环节，在相频曲线ω＝0＋处向上补画π/2 角。由开环传递函数可知P＝1。

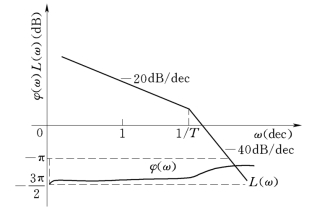
图5-44　例5-10 系统的开环对数频率特性曲线

由图可知，在L（ω）＞0dB的范围内，对应相频曲线从－π线开始向下变化，N＋＝0，N－＝1/2，则

所以闭环不稳定。

【例5-11】 已知系统开环传递函数

(www.xing528.com)

试用对数稳定判据判别闭环稳定性。

解：绘制系统开环对数频率特性曲线

先画出开环对数幅频渐近特性，然后再进行修正，因为振荡环节的阻尼比ζ＝0.1。在ω＝ωn 处振荡环节的对数幅频值为

系统开环对数幅频与相频曲线如图5-45所示。

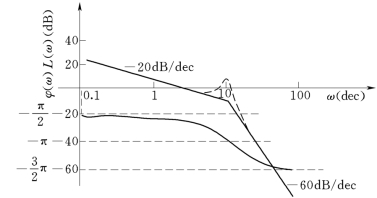
图5-45　例5-11 系统开环对数频率特性曲线

由于开环有一个积分环节，则在相频曲线ω＝0＋处向上补画π/2 角。P＝0。根据对数稳定判据，在L（ω）＞0dB 的范围内，对应相频曲线对－π线有一个负穿越，即，N＋＝0，N－＝1。

闭环不稳定。

闭环特征方程的正根数

Z＝P－2N＝0－2（－1）＝2

说明：对于最小相位系统还可以根据极坐标图和波德图的对应关系判断系统的稳定性。

【例5-12】 最小相位系统开环传递函数为：开环增益K 的大小对系统稳定性的影响如图5-46所示。

图5-46　K 增大时系统稳定性的变化

在图上可以看出，当K小时极坐标图不包围－1 点，系统是稳定的；K 取临界值时，极坐标图穿过－1 点，系统是临界稳定的；当K大时，极坐标图包围了－1 点，系统不稳定了。

从图上还可以看出，奈氏图穿过单位圆时，即当模为1 时，有：

稳定系统，相角大于－π。

临界稳定时，相角等于－π。

不稳定系统，相角小于－π。

作为等价描述，还可以解释成为，当相角为－π时：

稳定系统，模小于1。

临界稳定系统，模等于1。

不稳定系统，模大于1。

将上述情况表现在波德图上如图5-47所示。这样也可得到在波德图上的等价判据。

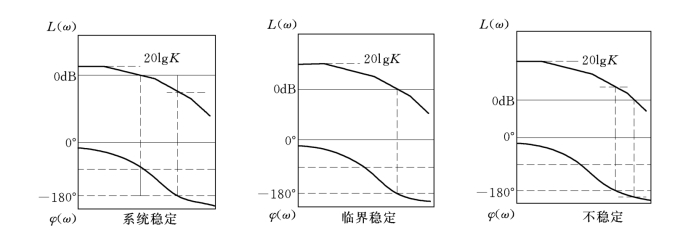
图5-47　波德图上的稳定性判据

当对数幅频特性穿过0dB线时，相角大于－π，即

则闭环系统是稳定的。

或者当对数相频特性为－π时。对数幅频特性小于0dB，即

则闭环系统是稳定的。

上述波德图上的等价判据，只适用于υ＝0 最小相位系统。对于其他系统，可以采用前面介绍的方法判断。

从上面的分析可以看到，利用波德图，不仅可以确定系统的绝对稳定性，而且还可以确定系统的相对稳定性。

如果是稳定系统，相位角还差多少度系统就不稳定了，或者增益再增大多少倍系统就不稳定了。

如果系统不稳定，相位角还需要改善多少度，或者增益值还需要减小到多大，不稳定系统就成为稳定系统了。

以上提出的有关稳定裕度的问题，正是在系统的设计中需要解决的问题。下面继续讨论上述问题的定量描述。