ElGamal加密算法的安全性分析

在ElGamal密码体制中，发送者A创建了r并把它保密；接收者B创建了x_B也把它保密。这种在算法的加密过程中引入随机数的方法增强了算法加密的不确定性，意味着相同的明文可能产生不同的密文，能够给攻击者制造破译的困难。

1.ElGamal的安全性表现

ElGamal密码体制的安全性具体表现在以下几个方面：

1）ElGamal密码体制的安全性基于有限域上的离散对数问题的困难性。离散对数计算是模幂运算的逆运算，求模幂运算容易，但计算有限域上的离散对数就相当困难了。

2）加密中使用的随机数r必须是一次性的；否则，攻击者获得r就能够在不知道私钥的情况下解密新的密文。

3）为了抵抗已知的攻击，要仔细地选择p，且g应是模p的本原元素，p应该至少是300位的十进制整数，并且p-1应该至少有一个较大的素数因子。

2.对ElGamal密码体制的攻击

针对ElGamal密码体制的攻击主要有两种方式：基于低模的攻击和基于已知明文的攻击。

（1）低模攻击

如果p的值不是足够大，攻击者可以运用一些有效的算法来解决求x_B或r的离散对数问题。如果p较小，攻击者可以很容易地求出x_B≡log_gy_B（mod p）并且把它保存起来，用它解密发给B的任何信息。只要B用的是相同的密钥，这个过程就可以一次完成。攻击者还可以运用c₁的值来求出A在每次传输r≡log_gc₁（mod p）时所用的随机数r的值。这两种情况都强调ElGamal密码体制的安全性依赖于使用大的模以保证解决离散对数问题的不可能性。

（2）已知明文攻击

如果A使用相同的随机指数r，加密两个明文m和m′，攻击者如果知道m就可以发现m′。假定

c₂≡m·y^r_B（mod p），c₂′≡m′·y^r_B（mod p）攻击者运用下面的步骤求出了m′：

y^r_B≡c₂·m^-1（mod p）

m′≡c₂′（y^r_B）-1（mod p）

为了阻止已知明文攻击，A应该用两个不同的r值来加密明文m和m′。

3.Shanks离散对数求法

ElGamal密码体制的安全性基于有限域上的离散对数问题的困难性。已知a^x≡y（mod p），求log_ay≡x（mod p）的运算就是离散对数计算问题。离散对数计算法有Shanks法、Pohlig-Hellman法和Pollard ρ法等。下面仅对Shanks离散对数求法作详细介绍。

在Shanks离散对数求法中，a和y是已知的，求满足y≡a^x（mod p）的x。为了求出x的值，可将x=[1，p-1]对应的全部a^x（mod p）都计算出来列成一张表格，比对哪一个值与y相同。这种解法实际是穷举搜索法，p很大时复杂度将很高。

如果a的乘法周期是n，即有aⁿ≡1（mod p），为了减少搜索范围，现在把n分成了d段，每段d个值，这里

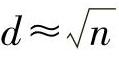
首先只在0≤r＜d内搜索满足a^r≡b（mod p）的那些r值。对于大于d的那些解x，可令

x=qd+r

再进行q轮的搜索，而q是整商，由于

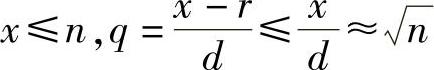
所以0≤q＜d。搜索轮数也不会大于d。这时

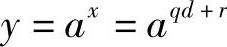
利用aⁿ≡1 mod p（n为周期），则

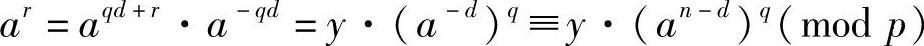
由于a、y已知，n、d也容易得知，利用上式，分别令q=0，1，2，3，…去测试，每次测试只在d个数据内搜索，总共最多搜索d轮。

总结以上内容，Shanks离散对数求法过程如下：(www.xing528.com)

1）选择，r←0，b←1；

2）将r和b≡a^r（mod p）列入表格；

3）若r=d-1，则对表格中b进行排序，转4）否则，b←ab（mod p），r←r+1，转2），结束；

4）计算A←a^n-d，B←y，q←0，开始下一轮；

5）若表格中存在数对（b，r），其中b=B，则x←qd+r输出x，结束否则，B←BA，q←q+1，转5）。

【例5-15】 已知y=3，a=5，求满足y≡a^x（mod 23）的x。

【解析】 把x=[1，22]对应的全部y≡5^x（mod 23）都计算出来，列入例5-12中的表5-1。从表中可以看出

5²²（mod 23）≡5⁰（mod 23）≡1（mod 23）

这正是费马定理a^p-1≡1（mod p）。它表明n=22是x的周期。同时表明原方程解的取值范围是0≤x＜n。

根据周期n=22，取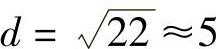，取r=0，1，2，3，4，对应b≡a^r（mod p）的值列入表5-2中，并对表格中b进行排序。

表5-2 b≡5^r（mod23）的部分解

计算 a^n-d=5^22-5=5¹⁷（mod 23）≡15

A←15

第一轮，q←0，y←3计算

b=a^r=y（a^n-d）0=3×15⁰=3

表中未查到b=3，于是B←3，令q←q+1，此时q=1。

第二轮，计算

b=y（a^n-d）1=y（a^n-d）0（a^n-d）=B×A=3×15（mod 23）≡22

表中仍未查到b=22。于是，B←22，令q←q+1，此时q=2。

第三轮，计算

b=y·（a^n-d）2=B×A=22×15（mod 23）≡8

表中还是未查到b=8。于是，B←8，令q←q+1，此时q=3。

第四轮，计算

b=y·（a^n-d）3=B×A=8×15（mod 23）≡5

表中查到了b=5对应的r=1，此时q=3。因此，结果是

x=qd+r=3×5+1=16

与穷举搜索法中结果一样

5¹⁶（mod 23）≡3

或 log₅3≡16（mod 23）