常见曲面方程及示例-微积分

现来看几个用向量建立常见的球面、圆柱面、圆锥面方程的例子.

例1　求以点M0（x0，y0，z0）为球心，半径为R的球面的方程.

解　如图7-17所示，设M（x，y，z）是球面上的任意一点，则有

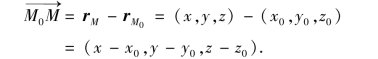
特殊地，球心在原点、半径为R的球面的方程为

图7-17

图7-18

例2　求以z轴为中心轴、半径为R的圆柱面的方程.

解　如图7-18所示，设M（x，y，z）是圆柱面上的任意一点，则点M在z轴上的投影点为M0（0，0，z），那么

例3　求顶点在原点，以z轴为中心轴、母线与z轴夹角为θ的圆锥面的方程.

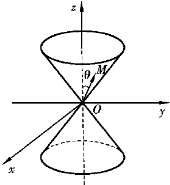
图7-19

通过例1、例2、例3以及7.3节的平面方程这些曲面的特例，可给出一般曲面方程的定义.

定义1　在空间解析几何中，任何曲面都可看成点的几何轨迹.在这样的意义下，如果曲面Σ与三元方程F（x，y，z）=0满足下述关系：

（1）曲面Σ上任一点的坐标都满足方程F（x，y，z）=0；

（2）不在曲面Σ上的点的坐标都不满足方程F（x，y，z）=0，则称方程F（x，y，z）=0为曲面Σ的方程.

定义2　曲线（或直线）绕某直线（称为旋转轴）旋转所得的曲面，称为旋转曲面.显然，球面、圆柱面、圆锥面都是旋转曲面.

如图7-20所示，若yOz面上的曲线F（y，z）=0（x=0），绕z轴旋转所得旋转曲面为Σ.设曲面Σ上任意一点为M（x，y，z），则点M（x，y，z）为yOz面上的点M0（0，y0，z）绕z轴旋转所得.点M0与M在z轴上的投影均为M1（0，0，z），且，所以，即

图7-20

(www.xing528.com)

又F（y0，z）=0，所以yOz面上的曲线F（y，z）=0（x=0）绕z轴旋转所得旋转曲面的方程为

同理，可得曲线yOz面上的曲线F（y，z）=0（x=0）绕y轴旋转所得旋转曲面的方程为

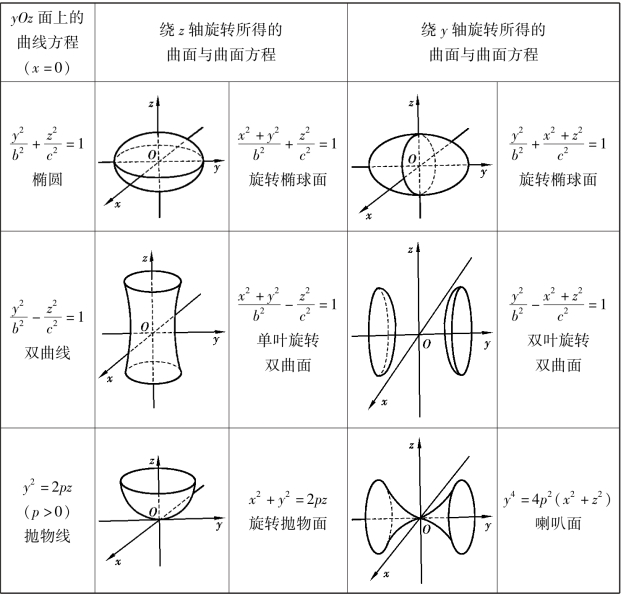
因此，可得到常见的yOz面上直线与二次曲线分别绕z轴及y轴旋转所得的旋转曲面方程，见表7-1.

表7-1　常见的yOz面上直线与二次曲线分别绕z轴及y轴旋转所得的旋转曲面方程

续表

下面介绍另一种重要的曲面——柱面.

定义3　直线与某一定曲线相交，并沿着此曲线平行移动的轨迹，称为柱面.该动直线称为柱面的母线，定曲线称为柱面的准线.

柱面与旋转曲面分别为直线与曲线运动的轨迹.直线保持过某一定点且与某一定曲线相交并沿此曲线运动的轨迹，称为锥面.同样，该动直线称为锥面的母线，定曲线称为锥面的准线，定点则称为锥面的顶点.圆锥面为锥面的一个特例，一般锥面不在此讨论.

下面只讨论准线为某坐标面上的曲线，且母线平行于与该坐标面垂直的坐标轴的柱面方程.

设xOy面上的曲线F（x，y）=0（z=0），则在空间中曲面方程

表示z可取任何实数，即曲面上的点（x，y，z）中，z可取任意值.而（x，y）满足F（x，y）=0，所以此曲面为母线平行于z轴、准线为曲线F（x，y）=0（z=0）的柱面方程.如例2中圆柱面x2+y2=R2为母线平行于z轴、准线为xOy面上的圆.

同理，可得曲面方程

为母线平行于x轴、准线为yOz面上的曲线F（y，z）=0（x=0）的柱面方程.

曲面方程

为母线平行于y轴、准线为zOx面上的曲线F（x，z）=0（y=0）的柱面方程.

常见的以二次曲线（椭圆、双曲线、抛物线）为准线的柱面方程及其图像见表7-2.

表7-2　常见的以二次曲线为准线的柱面方程及其图像

续表

显然，在椭圆柱面方程中，当a=b或a=c或b=c时，为圆柱面方程.因此，圆柱面仅是椭圆柱面的特例.