不确定机械问题的状态估计仿真结果

把本文所提出的摩擦状态估计器用于图5-2系统的仿真，该系统的动态模型为

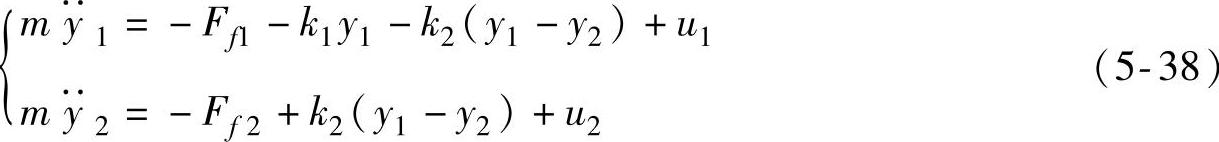
式中k₁和k₂——刚性弹簧系数；

F_f1和F_f2——摩擦力；

u₁和u₂——控制输入；

y₁和y₂——系统输出。设x，，x3=y2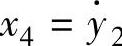，，那么上面的方程（5-38）能改写为如下形式

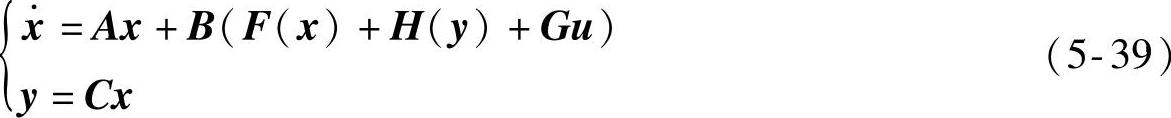
式中x=（x₁，x₂，x₃，x₄）T；

A=diag[A₁，A₂]；

B=diag[B₁，B₂]；

C^T=diag[C₁，C₂]；

u=（u₁，u₂）T，；；；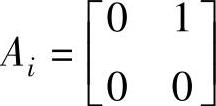

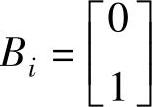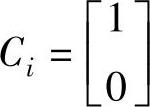i=1，2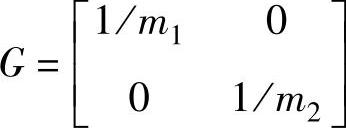；，F（x）=[F_f1/m₁，F_f2/m₂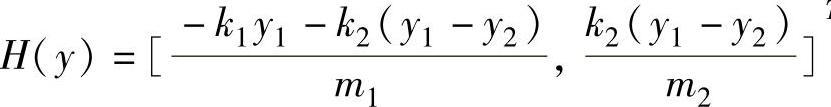]^T；T。

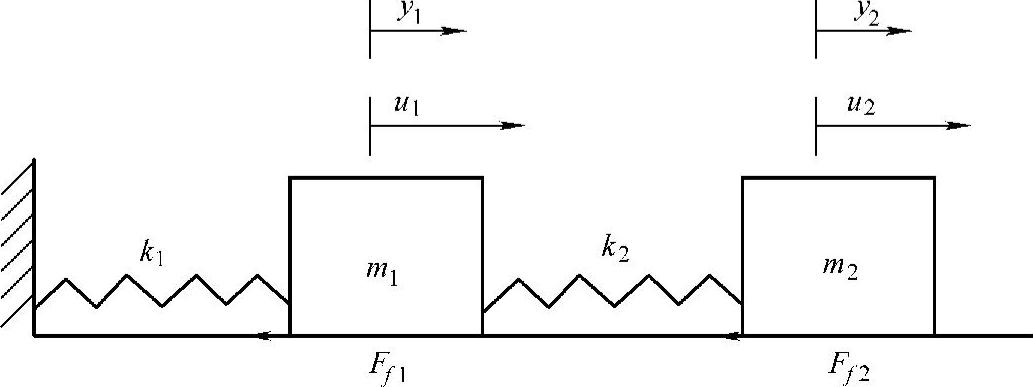
图5-2 二自由度系统的示意图

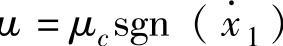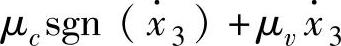仿真过程的摩擦力F_fi=μF_N，其摩擦因数μ的三种模型：①μ。②μ=。③。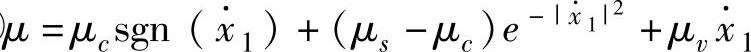

在第一个仿真里，图5-2中的F_f1和F_f2摩擦模型分别取Couloumb模型和Couloumb+Viscous摩擦模型。在另一个仿真里，将图5-2中F_f1的Couloumb模型换成一个较复杂的摩擦模型，也就是Stribeck模型，进一步考察系统的观测性能。表5-1是三种摩擦模型的参数定义及给定值。

表5-1 摩擦模型参数与结构

步骤1.变量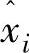的隶属度函数选择如下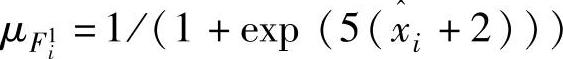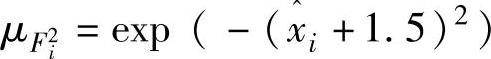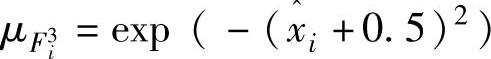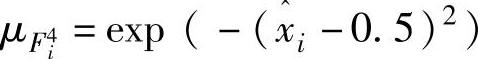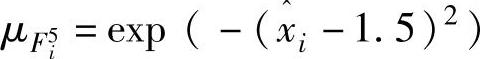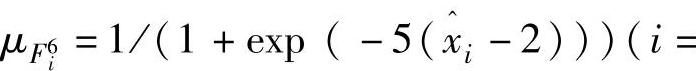：，，，，，1，2，3，4）。

建立如下的模糊规则库：

1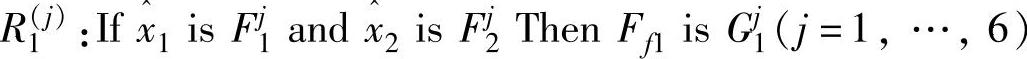）。(https://www.xing528.com)

2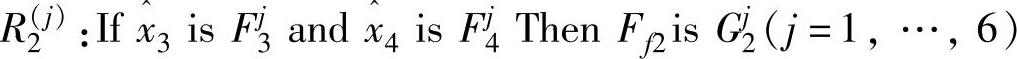）。设

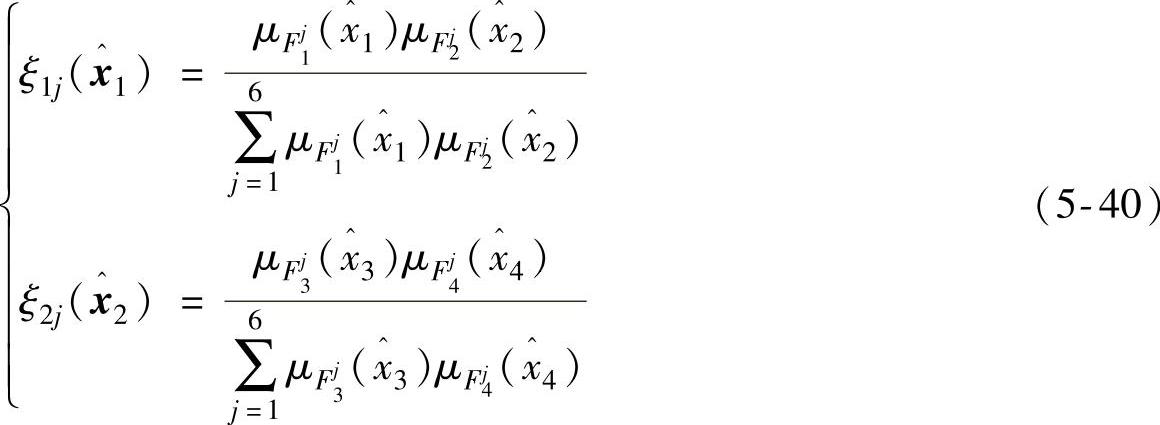
那么得到下面的模糊基函数：

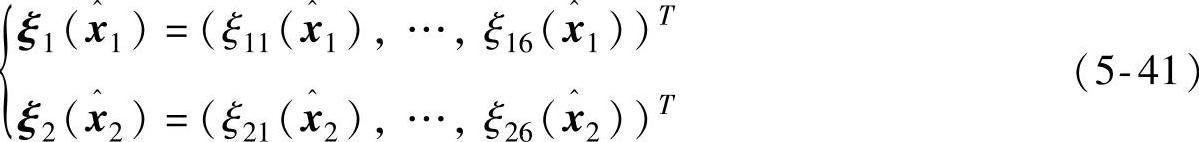
步骤2.系统仿真参数选择：

γ=100，L^-1=1/（S+3），ρ=15，x（0）=（0.5，0.0，-0.5，0.0）T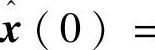，（0.0，0.0，0.0，0.0）T，K_o=[8918400；0089184]^T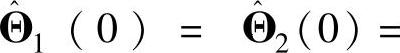，（-8，-6，-1，3，8，1）T。

步骤3.求解方程（5-22），可得摩擦建模状态估计器

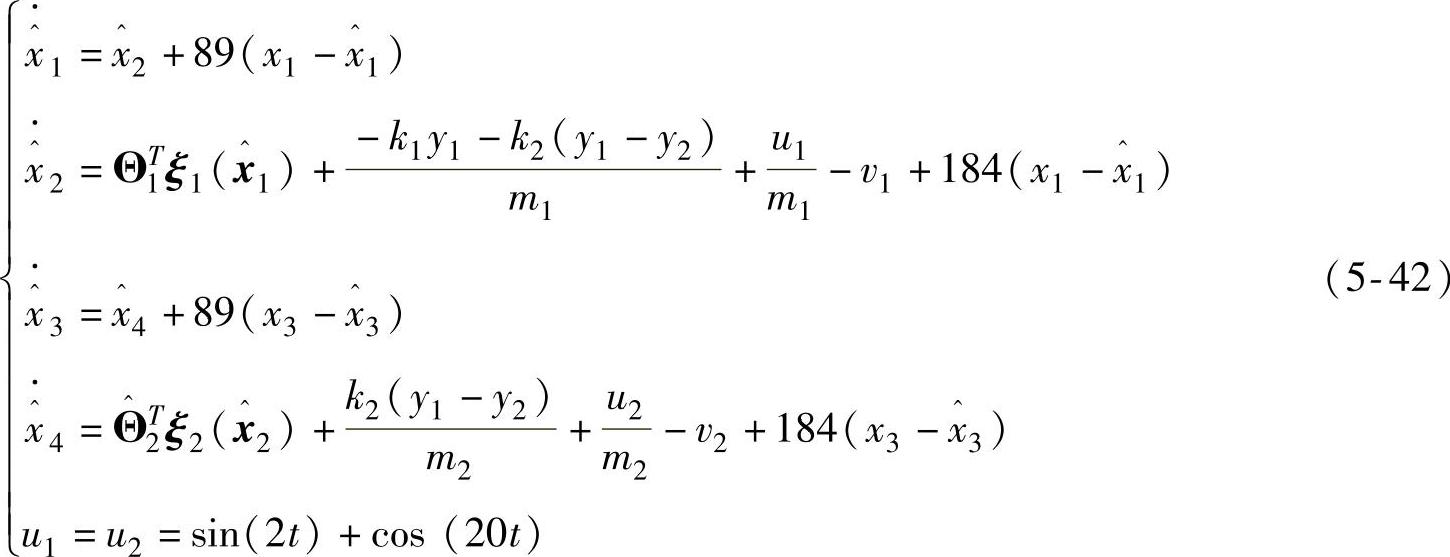
步骤4.选择下面的参数自适应律

图5-3是图5-2中的F_f1和F_f2分别取Couloumb和Couloumb+Viscous摩擦时，状态估计器所估计的位置与速度曲线和实际曲线。而图5-4是图5-2中的F_f1和F_f2分别取Stribeck和Couloumb+Viscous摩擦时，状态估计器所估计的位置与速度曲线和实际曲线。在前面两个仿真里，鲁棒补偿控制项为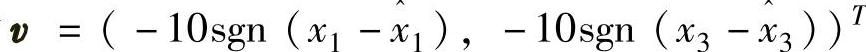，m1=m2=1.00kg，k₁=1.0N/m，k₂=2.0N/m。

图5-5是图5-2中的F_f1和F_f2分别取Couloumb和Couloumb+Viscous摩擦时，状态估计器所估计的位置与速度曲线和实际曲线。而图5-6是图5-2中的F_f1和F_f2分别取Stribeck和Couloumb+Viscous摩擦时，状态估计器所估计的位置与速度曲线和实际曲线。在后面两个仿真里，鲁棒补偿控制项为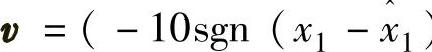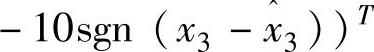），，m1=0.20kg，m₂=0.25kg，k₁=100.0N/m，k₂=200.0N/m。

从这四个仿真结果可以看出，无论摩擦力取Couloumb摩擦模型、Couloumb+Viscous摩擦模型、Stribeck摩擦模型，还是系统的质量和弹簧刚性参数在变化，我们所设计的摩擦状态估计器具有良好的状态估计效果，具有良好的自适应特性，完全可以用该估计状态对摩擦进行建模与控制补偿。

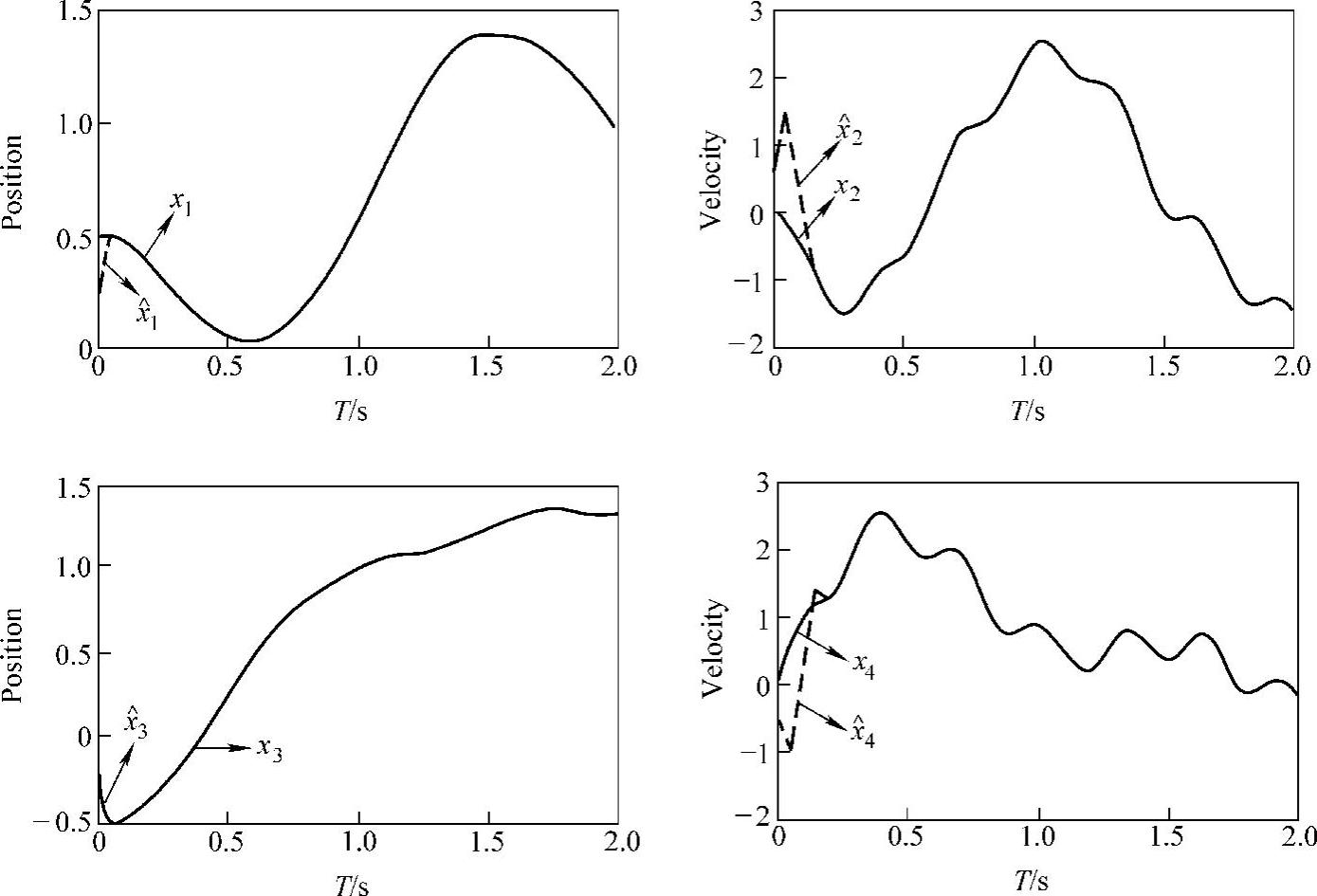
图5-3 实际状态x和估计状态x^

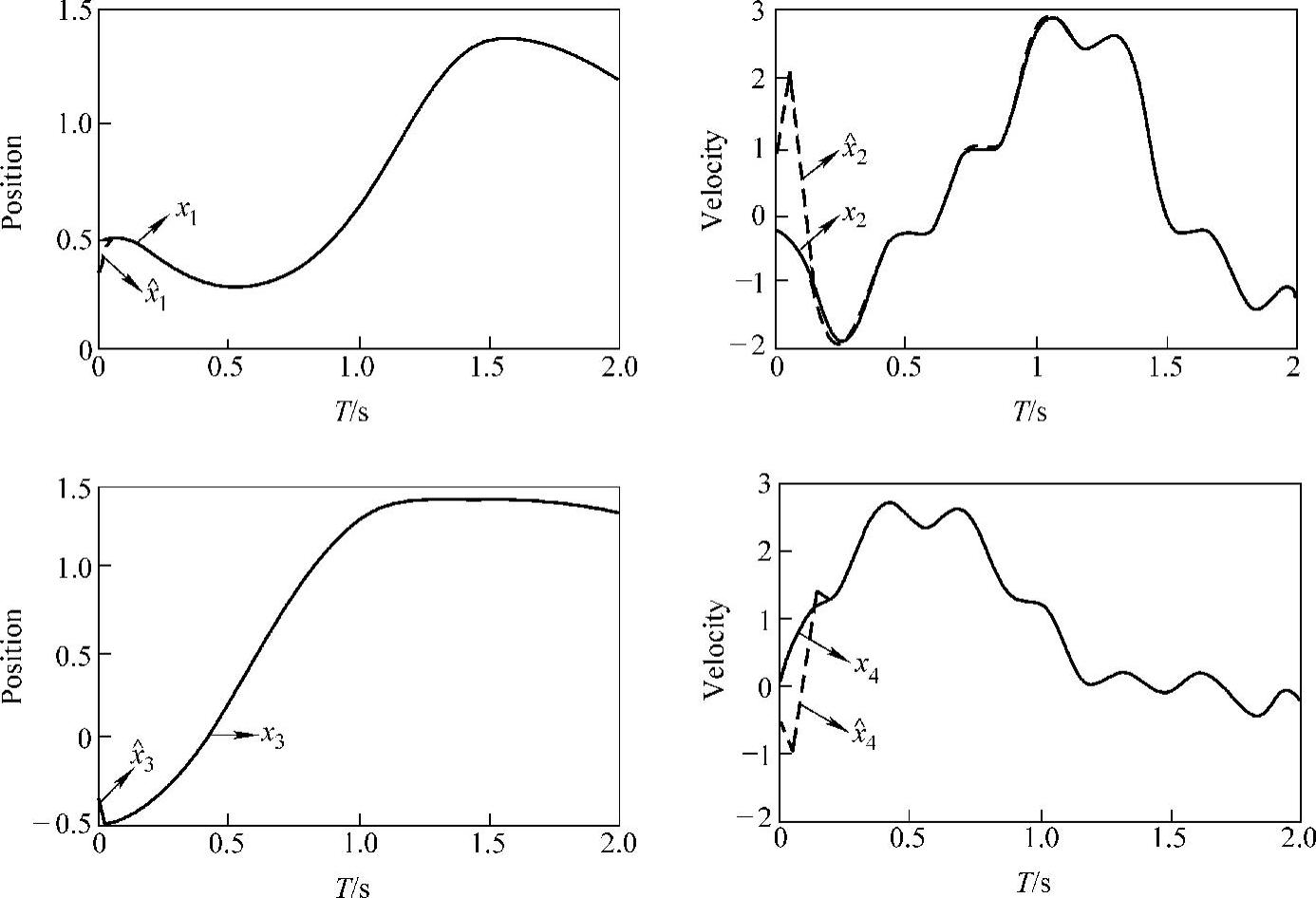
图5-4 实际状态x和估计状态x^

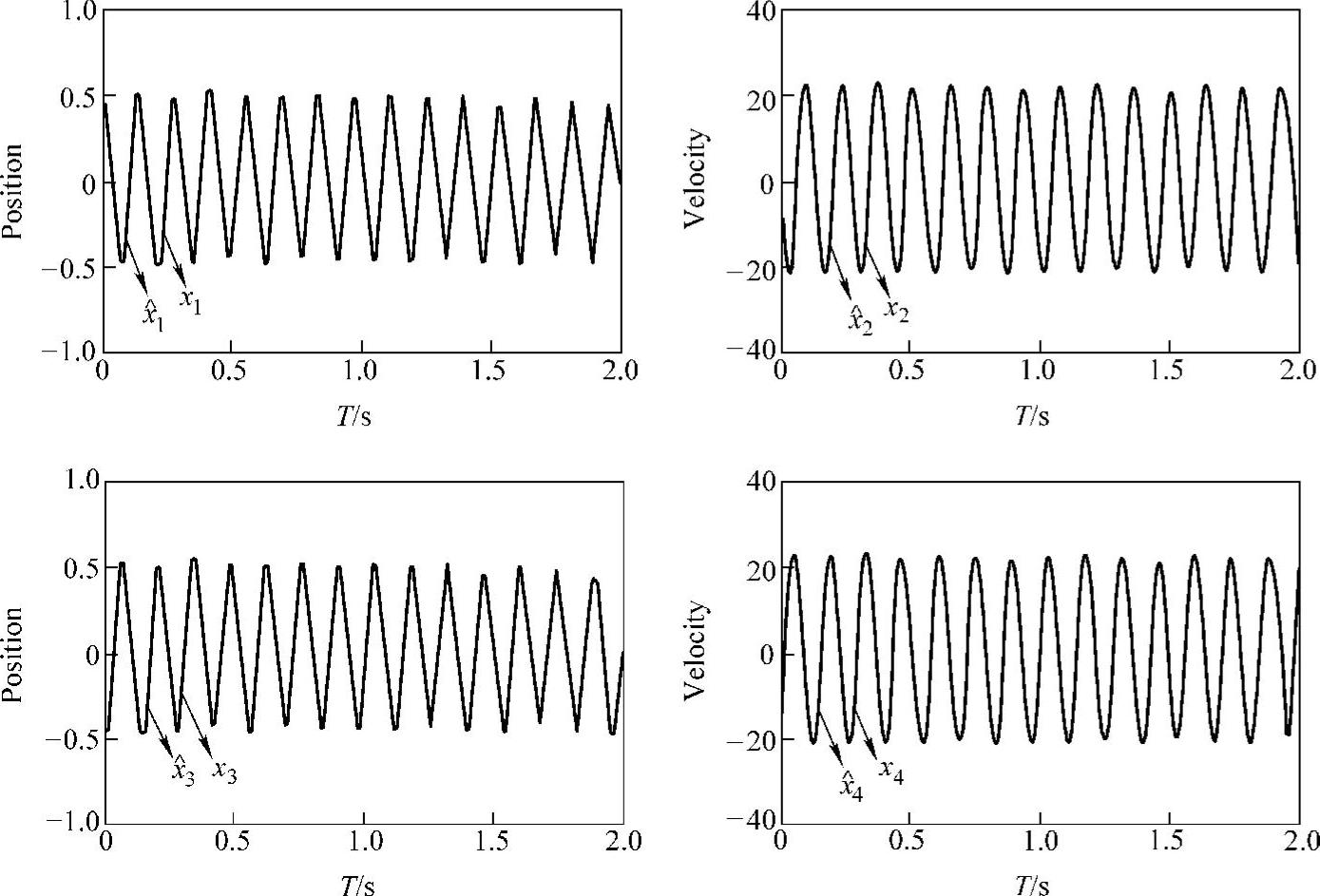
图5-5 实际状态x和估计状态x^

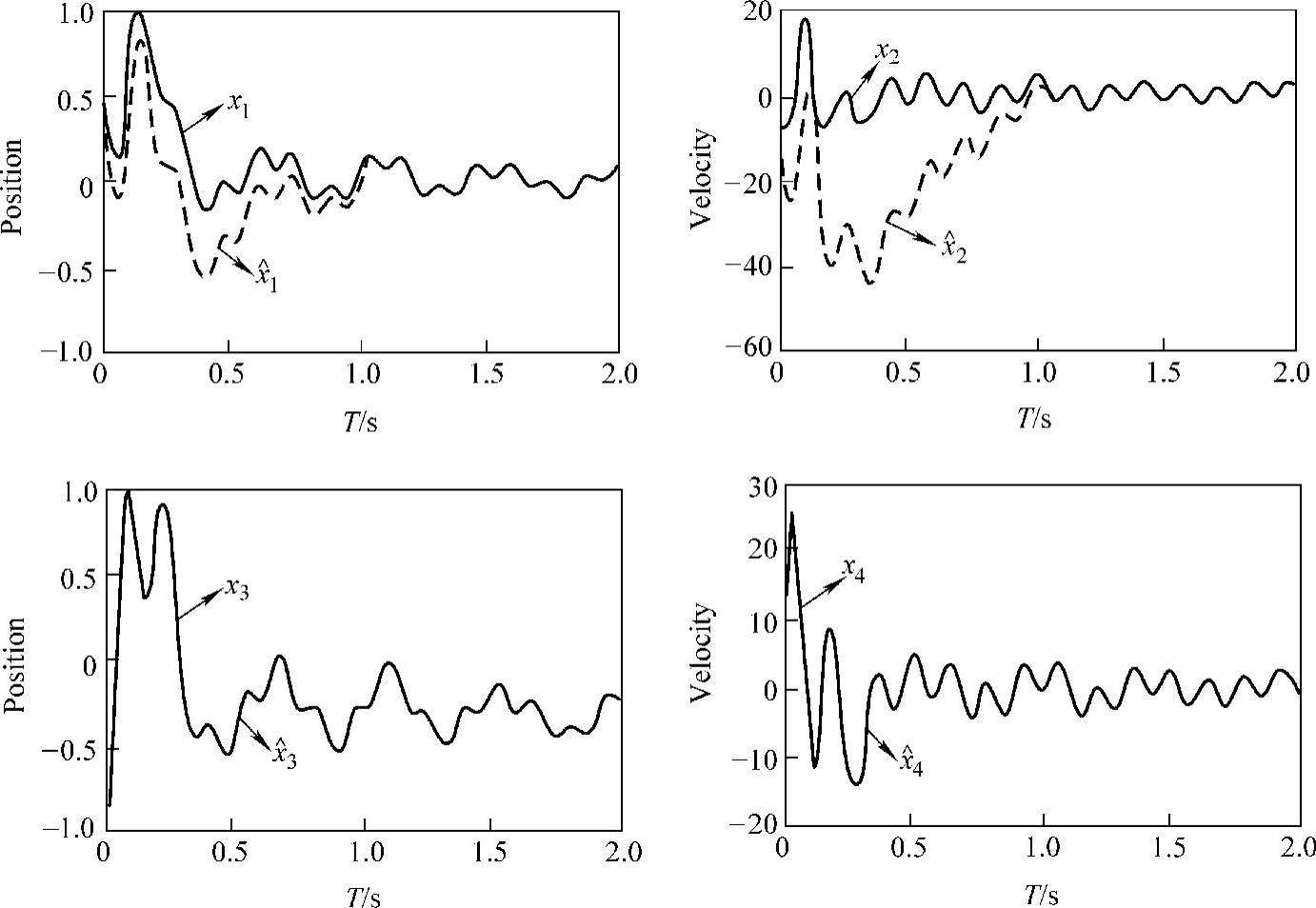
图5-6 实际状态x和估计状态x^