弦振动方程的导出及应用

弦振动方程实际上是一维波动方程。弦振动方程是在18世纪由达朗贝尔等人首先给予系统研究的。它是一大类偏微分方程的典型代表。本节主要介绍弦振动方程的数学描述。

问题描述：假设一根长度为l、两端固定拉紧的均匀柔软的细弦，当弦在外力作用下在平衡位置附近做微小的横振动时，求弦上各点的振动情况。

物理规律：

（1）动量定理。物体动量的增量等于它所受合外力的冲量。

（2）胡克（Hooke）定律。材料在弹性变形阶段，其应力和应变成正比例关系。

将实际问题归结为数学模型时，必须做一些理想化的假设，以便抓住问题最本质的特征。在考察弦振动问题时的基本假设如下：

（1）弦是均匀的，弦的截面直径与弦的长度相比可以忽略，因此弦可以视为一根曲线，它的（线）密度ρ是常数。

（2）弦在某一平面内做微小横振动，即弦的位置始终在一直线段附近，而弦上各点均在同一平面内垂直于该直线的方向上做微小振动，弦偏离平衡位置的位移量远远小于弦的长度。

（3）弦是柔软的，且有弹性的，张力方向与弦振动波形的切线方向一致，张力在法线方向无分力，而弦的伸长形变与张力的关系服从胡克定律。

（4）弦是拉紧的，弦上任一小段微元都不能再拉伸，由胡克定律可知，张力是常量。

当弦不振动时是一条直线，取这条直线作为坐标系的x轴，垂直于x轴的方向作为弦的振动方向，以u（x，t）表示弦在任意一点x处任意时刻t的位置，如图2.1所示。

弦在张力的作用下开始振动，在弦上任取一弦段（x，x＋Δx），它的弧长为

由基本假设（2）知很小，于是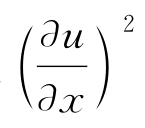为高阶小量，因此

图2.1　弦的振动示意图

点x处的张力记为T（x），其模长记T（x），点x处弦的左边部分对右边部分的拉力与弦的右边部分对左边部分的拉力大小均为T（x）。根据假设，张力T（x）的方向总是沿着x处的切线方向。作用于弦段（x，x＋Δx）的张力在x、u两个方向上的分力分别为

－T（x）cosα1，－T（x）sinα1

式中，α1为张力T（x）的方向与水平线的夹角；负号表示力的方向取与坐标轴相反的方向。在弦段的另一端x＋Δx点处作用于弦段（x，x＋Δx）的张力在x、u两个方向的分力分别为

T（x＋Δx）cosα2，T（x＋Δx）sinα2

式中，α2为张力T（x＋Δx）与水平线的夹角。

由于弦只在x轴的垂直方向做横振动，故水平方向的合力为零，即

由于假设弦仅在平衡位置附近做微小振动，所以

于是，式（2.2）变为

故T（x＋Δx）＝T（x）＝T，也就是说，T是一个常数。又由基本假设（2）知

所以张力在x轴垂直方向的合力为

从而在时间段（t，t＋Δt）内该合力产生的冲量为

在时刻t弦段（x，x＋Δx）的动量为

在时刻t＋Δt该弦段的动量为

所以从时刻t到时刻t＋Δt，弦段（x，x＋Δx）的动量增加量为

根据动量定理，

从而

由Δx，Δt的任意性可知式（2.10）中的被积函数必须为零，从而得到

记为a2，不受外力作用时弦振动所满足的方程

不受外力作用时弦振动方程即为一维齐次波动方程。

如果弦在振动过程中还受到一个与弦的振动方向平行的外力，假定单位长度所受的外力为F（x，t），则弦段（x，x＋Δx）上所受外力为(www.xing528.com)

它在时间段（t，t＋Δt）内所产生的冲量为

根据动量定理，时间段（t，t＋Δt）内外力产生的冲量和张力产生的冲量之和等于弦段动量的改变量，即

仍由Δx，Δt的任意性知

外力作用下弦振动所满足的方程为

外力作用时弦振动方程即为一维非齐次波动方程。f（x，t）称为自由项，是由于振动中有外力作用而产生的，因此f≡0的情况对应于自由振动；而f≠0的情况对应于强迫振动。

例2.1　细杆（或弹簧）受某种外界原因而产生纵向振动，以u（x，t）表示静止时在x处的点在时刻t离开原来位置的偏移，假设振动过程发生的张力服从胡克定律，试证明u（x，t）满足方程

其中ρ为杆的密度，E为杨氏模量。

证明　在杆上任取一段，其中两端于静止时的坐标分别为x与x＋Δx。现在计算这段杆在时刻t的相对伸长。在时刻t这段杆两端的坐标分别为

x＋u（x，t），x＋Δx＋u（x＋Δx，t＋Δt）

其相对伸长等于

令Δx→0，取极限，在点x的相对伸长为ux（x，t）。由胡克定律，张力

T（x，t）＝E（x）ux（x，t）

式中，E（x）为在点x的杨氏模量。

设杆的横截面面积为S（x），则作用在杆段（x，x＋Δx）两端的力分别为

E（x）S（x）ux（x，t），E（x＋Δx）S（x＋Δx）ux（x＋Δx，t）

于是得运动方程

ρ（x）S（x）·Δx·utt（x，t）

＝E（x＋Δx）S（x＋Δx）ux（x＋Δx，t）－E（x）S（x）ux（x，t）

利用微分中值定理，消去Δx，再令Δx→0得

若s（x）＝常量，则得

即得所证。

例2.2　绝对柔软而均匀的弦线有一端固定，在它本身重力作用下，此线处于铅垂平衡位置，试导出此线的微小横振动方程。

解　设弦长为l，弦的线密度为ρ，当弦不振动时为一条直线，取这条直线为x轴，以u（x，t）表示弦在任意点x任意时刻t的位移，此时x点处的张力T（x）为

T（x）＝ρg（l－x）

且T（x）的方向总是沿着弦在x点处的切线方向。仍以u（x，t）表示弦上各点在时刻t沿垂直于x轴方向的位移，取弦段（x，x＋Δx），则弦段两端张力在u轴方向的投影分别为

ρg（l－x）sinθ（x），ρg［l－（x＋Δx）］sinθ（x＋Δx）

其中θ（x）表示T（x）方向与x轴的夹角。

又

在（t，t＋Δt）时段内，弦段（x，x＋Δx）所受的冲量为

动量的变化量为

当Δx→0时，根据动量守恒，可得

得