线性方程的叠加原理及应用

如果算子L满足可加性条件

L［C1u1＋C2u2］＝C1L［u1］＋C2L［u2］

其中C1，C2为任意给定的常数，则称算子L是线性的。

如果L是线性微分算子，那么方程

Lu＝f

称为线性微分方程。特别地，当f≡0时，方程

Lu＝0

称为齐次的。

如果定解条件满足可加性条件，那就称定解条件是线性的。在前面各章中所遇到的各种定解条件（如柯西问题，第一、第二、第三边值问题等的定解条件）都是线性的。同样可以定义齐次定解条件。

对于线性方程（或线性定解条件），下面的叠加原理是显然的。

叠加原理1　设ui满足线性方程（或线性定解条件）

Lui＝fi　（i＝1，…，n）

则它们的线性组合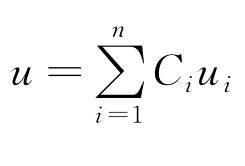（其中C1，…，Cn为任意给定的常数）必满足方程（或定解条件）

特别地，当ui（i＝1，…，n）满足齐次方程（或齐次定解条件）时，u也满足此齐次方程（或齐次定解条件）。(www.xing528.com)

在前面的讨论中，我们曾多次利用这个叠加原理，把一些复杂的定解问题化为若干简单的定解问题来求解。例如在求解非齐次方程（或非齐次定解条件）的问题中，常通过找一个满足方程（或定解条件）的函数把它化为齐次方程（或齐次定解条件）的相应问题来解决。

在实际应用中，我们不仅用有限个特解的叠加来做出问题的解，更多的情况是用无限个特解来叠加，这时就得到用级数或积分表示的（形式）解。自然在后一情况，还必须证明这些级数或积分是收敛的，而且的确是问题的解。这样，上面的叠加原理常拓广成下面的形式，在实际问题中加以应用。

叠加原理2　设ui满足线性方程（或线性定解条件）

Lui＝fi　（i＝1，2，…）

又假设它们的线性组合满足一定的条件[1]，那么u满足方程（或定解条件）

特别地，当ui（i＝1，2，…）满足齐次方程（或齐次定解条件）时，u也满足此齐次方程（或齐次定解条件）。

叠加原理3　设u（M，M0）满足线性方程（或线性定解条件）

Lu＝f（M，M0）

其中M0为参数，又假设U（M）＝∫u（M，M0）dM0满足一定的条件[2]，那么U（M）满足方程（或定解条件）

LU（M）＝∫f（M，M0）dM0

特别地，当u满足齐次方程（或齐次定解条件）时，U也满足此齐次方程（或齐次定解条件）。

这些叠加原理是线性方程许多重要解法的基础。例如，当用分离变量法解齐次方程时，就是利用方程和边界条件的齐次与线性的性质，把解表示为满足方程和边界条件的一系列特解的叠加，并使其和恰好符合初始条件。又如，在用齐次化原理求非齐次方程的解时，也是把非齐次方程的解视为一系列在特定初始条件下齐次方程的解的叠加而构造得到的。傅里叶变换法与格林函数法，也利用了叠加原理这一基本性质。

对非线性方程（或者是线性方程具有非线性定解条件）的情形，叠加原理不成立。此时，在线性问题中许多行之有效的方法就不能直接使用，而必须另外寻求新的方法，所以对于非线性方程的讨论往往比线性方程要困难得多。