多元函数极值与条件极值，高等数学应用

1.多元函数的极值及其求法

设函数z=f(x,y)在点(x0,y0)的某个邻域内有定义,如果对该邻域内任何异于(x0,y0)的点(x,y),都有

则称函数在点(x0,y0)有极大值(或极小值)f(x0,y0).极大值、极小值统称极值.使函数取得极值的点称为极值点.使fx(x,y) =0,fy(x,y) =0 同时成立的点(x0,y0)称为函数的驻点.二元函数的极值点可能是驻点,也可能是偏导数至少有一个不存在的点.

例如,旋转抛物面z=f(x,y) =x2 +y2,点(0,0)是驻点,且(0,0)处有极小值0.

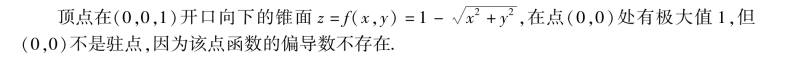
与一元函数极值类似,关于二元函数极值有以下定理:

定理8.5(必要条件)　设函数z=f(x,y)在点(x0,y0)具有偏导数,且在点(x0,y0)处有极值,则

几何上看,驻点(x0,y0)处曲面z=f(x,y)有切平面z=z0 平行于xOy 坐标面,即

由定理8.5 可知,具有偏导数的函数的极值点必定是驻点,但驻点不一定是极值点.

例如,函数z=f(x,y) =xy(马鞍面),偏导数fx =y,fy =x,点(0,0)是函数的驻点,但函数在点(0,0)处既不取得极大值也不取得极小值,因为f(0,0) =0,而在(0,0)的任意邻域内f(x,y)既能取到正值也能取到负值.

定理8.6(充分条件)　设函数z=f(x,y)在点(x0,y0)的某邻域内连续且有一阶及二阶连续偏导数,且fx(x0,y0) =0,fy(x0,y0) =0,记作

则:

(1)AC-B2 ＞0 时,f(x0,y0)取得极值.且当A ＜0 时,f(x0,y0)为极大值;当A ＞0 时,f(x0,y0)为有极小值.

(2)AC-B2 ＜0 时,f(x0,y0)不取极值.

(3)AC-B2 =0 时,f(x0,y0)可能有极值,也可能没有极值(证明略).

二元函数极值的求法:

(2)对每一个驻点(x0,y0),求出二阶偏导数的值A,B 和C.

(3)由AC-B2 的符号,判定f(x0,y0)是否极值、极大值、极小值.

如果有偏导数不存在的点,也应根据实际问题判断是否取得极值.

例4　求函数f(x,y) =x3 +y3 -3xy 的极值.

解　解方程组

得驻点为(1,1),(0,0),则

在点(1,1)处,AC -B2 =27 ＞0,又A ＞0,函数在(1,1)处有极小值f(1,1) = -1;在点(0,0)处,AC-B2 = -9 ＜0,所以f(0,0)不是极值.

2.多元函数的最大值、最小值及其求法

如果f(x,y)在有界闭区域D 上连续,则f(x,y)在D 上必定能取得最大值和最小值.求最大值和最小值的方法是:将函数f(x,y)在D 内的所有驻点和不可导点处的函数值及函数在D的边界上的最大值和最小值作比较,其中最大的就是最大值,最小的就是最小值.在实际问题中,如果根据问题的背景,知道函数f(x,y)的最大值(最小值)一定在D 的内部取得,而函数在D 内只有一个驻点,那么可肯定该驻点处的函数值就是函数f(x,y)在D 上的最大值(最小值).

例5　求函数z=3x2 +3y2 -x3 在x2 +y2≤16 上的最值.

解　在区域x2 +y2 ＜16 内求极值,解方程组

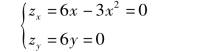
得驻点(0,0)和(2,0).又

在点(0,0),AC-B2 =36 -0 =36 ＞0,又A=6 ＞0,故点(0,0)是极小值点.

在点(2,0),AC-B2 = -36 -0 = -36 ＜0,故点(2,0)不是极值点.

因此,f(0,0) =0 是极小值.在x2 +y2 =16 上求极值:将y2 =16 -x2代入函数,则

因为z′x = -3x2≤0,即z=48 -x3 在[ -4,4]上为单调递减函数,所以:

z 在x2 +y2 =16 上的最小值为

z 在x2 +y2 =16 上的最大值为

经比较可知,z 在x2 +y2≤16 上的最小值为-16,最大值为112.

例6　生产甲乙两种产品,销售单价分别为10 万元和9 万元.若生产x 件甲种产品和y 件乙种,产品的总成本为

求企业获得最大利润时两种产品的产量各为多少?

解　设总利润为L(x,y),则

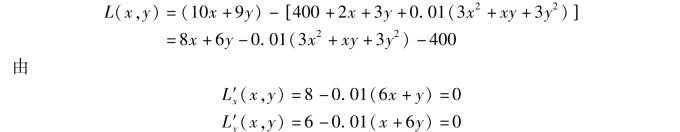
得驻点(120,80),则

(www.xing528.com)

有

因此,当x=120,y=80 时,L(120,80) =320 是极大值(也是最大值).

获得最大利润时,甲种产品生产120 件,乙种产品生产80 件.

例7　用钢板做一个容积为V 的无盖长方形水箱,问怎样选择水箱的长、宽、高才使用料最省?

解　设水箱长、宽、高分别为x,y,z,D:0 ＜x ＜+∞,0 ＜y ＜+∞.

或求二阶偏导数

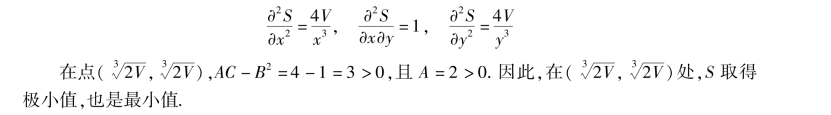
3.条件极值与拉格朗日乘数法

上面讨论的极值问题,对自变量除了限制在定义域内以外,没有其他条件限制,称这类极值为无条件极值.如果除了函数z=f(x,y)的定义域外,对自变量还有附加条件φ(x,y) =0 的极值称为条件极值.

条件极值由(目标)函数与条件构成,可表示为

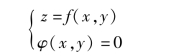
条件极值可由条件解得一个变量的表达式,将其代入目标函数就化为一元函数最值问题,按一元函数求最值的方法可求得解.但在很多情形下,将条件极值化为无条件极值并不容易.这里介绍另一种求条件极值的方法,这就是拉格朗日乘数法.

拉格朗日乘数法:要找函数z=f(x,y)在条件φ(x,y) =0 下的可能极值点,首先构造辅助函数

其中,λ 为一常数;然后求函数F(x,y,λ)的无条件极值,即解方程组

由方程组解出x,y,λ,则(x,y)就是可能的极值点.至于如何确定所求的点是否极值点,在实际问题中往往可根据问题本身来判定.

例8　在本节的例6 中增加一个附加条件,两种产品的总产量为100 件,企业获得最大利润时两种产品的产量各为多少?

解　设条件极值

其中

拉格朗日乘数法,作

解方程组

得

即两种产品生产100 件,获得最大利润时,需要生产甲种产品70 件,乙种产品30 件.

注　此题也可由条件解得一个变量,将其代入利润函数,化为一元函数求最值.

*例9　求表面积为a2 而体积最大的长方体的体积.

解　设长方体的长、宽、高分别为x,y,z,则条件极值

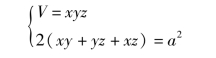
构造辅助函数

解方程组

*例10(最小二乘法)　设由观测或实验得到一系列数据点(xi,yi)(i =1,2,…,n),它们大体上在一条直线附近,即可用一条直线方程近似反映变量x 与y 之间的相关关系(见图8.12).现要确定这一条直线,使其与这n 个点的偏差平方和达到最小(最小二乘法).

图8.12

解　设所求直线方程为

由测得的n 个数据(xi,yi)(i=1,2,…,n),确定a,b,使偏差平方和

为最小.因此,令

整理并求解线性方程组,得

求此方程组的解,即得f(a,b)的驻点