函数极限的定义及其研究形式

因为数列｛x_n｝可看作自变量为n的函数

x_n=f（n），n∈N^∗

所以由数列极限的定义引出函数极限的一般概念，即在自变量的某个变化过程中，如果对应的函数值无限接近于某个确定的数，那么这个确定的数就叫作在这一变化过程中函数的极限.由于自变量的变化过程不同，函数的极限也表现为不同的形式.对于函数的极限主要研究两种情形：

（1）自变量x无限接近于x₀或者说趋近于x₀（记作x→x₀）时，对应的函数值f（x）的变化情况.

（2）自变量x的绝对值x无限增大，即趋于无穷大（记作x→∞）时，对应的函数值f（x）的变化情况.

1.自变量x趋于x₀时函数的极限

现在考虑如果函数y=f（x）在x→x₀的过程中，对应的函数值f（x）无限接近于确定的数值A，那么就说A是函数f（x）当x→x₀时的极限.这里我们首先假定函数f（x）在x₀的某个去心邻域内有定义.

由数列极限的定义可以过渡到函数极限的定义.也就是说，在x→x₀的过程中，函数f（x）无限接近于A，就是∣f（x）-A∣能任意小，即对于任意小的正数ε，f（x）-A＜ε.而x→x₀可表达为0＜∣x-x₀∣＜δ，其中δ是某个正数.从几何上来看，是适合不等式

0＜∣x-x₀∣＜δ

的x的全体，即点x₀的去心δ邻域，而邻域半径δ体现了x接近x₀的程度.因此有如下的定义：

定义1 设函数f（x）在点x₀的某个邻域内有定义，如果存在常数A，对于任意给定的正数ε（无论它多么小），总存在正数δ，使得当x满足不等式0＜∣x-x₀∣＜δ时，对应的函数值f（x）都满足不等式

∣f（x）-A∣＜ε

那么常数A就叫作函数f（x）当x→x₀时的极限，记作

特别指出，定义1中的0＜∣x-x₀∣＜δ表示x≠x₀，所以x→x₀时f（x）有没有极限与f（x）在点x₀是否有定义并无关系.

定义1也可简单表述为

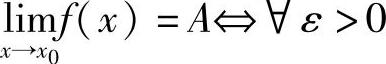，∃δ＞0，当0＜∣x-x₀∣＜δ时，有∣f（x）-A∣＜ε

函数f（x）当x→x₀时的极限为A的几何解释（见图1-10）：任给正数ε，构建平行于x轴的两条平行直线y=A+ε和y=A-ε，介于这两条直线间的是一横条区域.根据定义，对于任给ε，存在点x₀的一个δ邻域（x₀-δ，x₀+δ），当y=f（x）的图像上点的横坐标x在邻域（x₀-δ，x₀+δ）内，但x≠x₀时，这些点的纵坐标f（x）满足不等式

∣f（x）-A∣＜ε

或 A-ε＜f（x）＜A+ε

例1 证明：.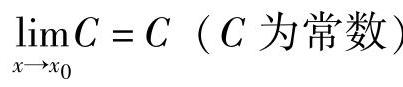

证明 ∀ε＞0，要使

∣f（x）-C∣=∣C-C∣=0＜ε

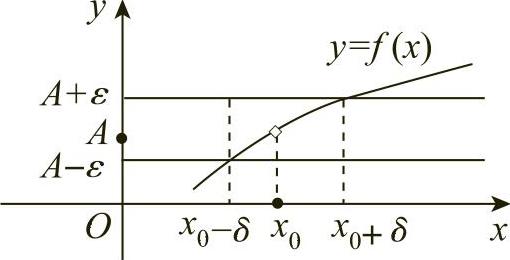
图1-10

只需要取δ=ε，则当0＜∣x-x₀∣＜δ时，有

∣f（x）-C∣＜ε

所以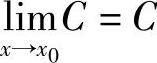

例2 证明：.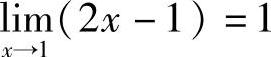

证明∀ε＞0，要使

∣f（x）-1∣=∣2x-1-1∣=2∣x-1∣＜ε

只需要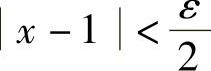

因此取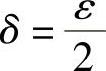，则当0＜∣x-1∣＜δ时，对应的函数值f（x）满足不等式

f（x）-1＜ε

所以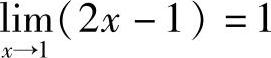

例3 证明：.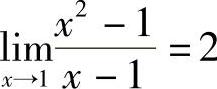

证明 ∀ε＞0，要使

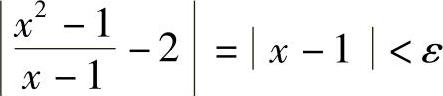
只需要取δ=ε，则当0＜∣x-1∣＜δ时，有

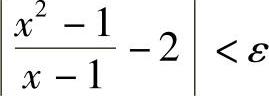
所以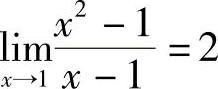

例4 证明：当x₀＞0时，.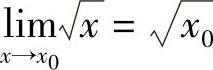

证明 ∀ε＞0，因为

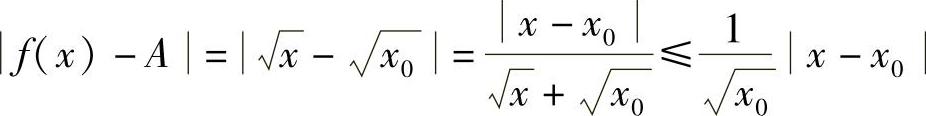
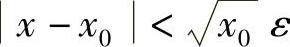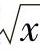要使∣f（x）-A∣＜ε，只需要.另一方面，为使x≥0，只需要∣x-x₀∣≤x₀.因此取，则当0＜∣x-x₀∣＜δ时，对应的函数值满足不等式(www.xing528.com)

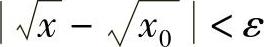
所以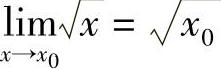

在x→x₀时，函数f（x）的极限概念中，x既从x₀的左侧也从x₀的右侧趋于x₀，但有时只能或只需要考虑x仅从x₀的左侧趋于x₀（记作x→x₀^-）的情形，或x仅从x₀的右侧趋于x₀（记作x→x₀⁺）的情形，从而有了左、右极限的概念.

设函数f（x）在点x₀的某个左邻域内有定义，如果存在常数A，若∀ε＞0，∃δ＞0，当x₀-δ＜x＜x₀时，有

∣f（x）-A∣＜ε

则称A为x→x₀^-时函数f（x）的左极限，记为

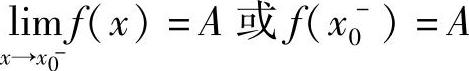
设函数f（x）在点x₀的某个右邻域内有定义，如果存在常数A，若∀ε＞0，∃δ＞0，当x₀＜x＜x₀+δ时，有

∣f（x）-A∣＜ε

则称A为x→x₀⁺时函数f（x）的右极限，记为

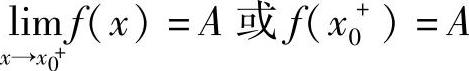
函数的左、右极限统称为单侧极限.

根据x→x₀时函数f（x）的极限定义，以及左、右极限的定义，容易证明：函数f（x）当x→x₀时极限存在的充分必要条件是左、右极限存在且相等，即

f（x₀^-）=f（x₀⁺）

因此，即使f（x₀^-）和f（x₀⁺）都存在，但若不相等，那么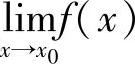也不存在.

例5 函数

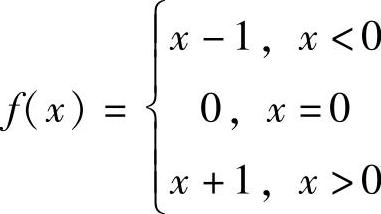
当x→0时，f（x）的极限不存在.

实际上，

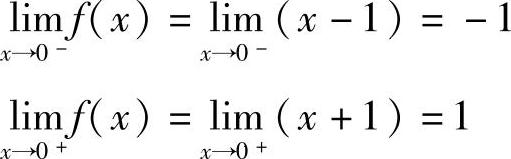
因为左、右极限存在但不相等，所以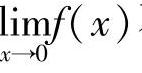不存在，如图1-11所示.

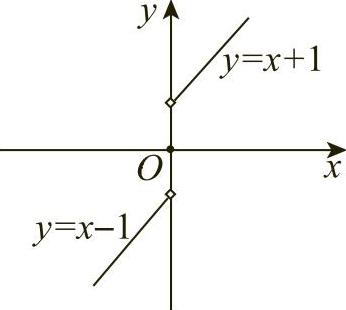
图1-11

2.自变量趋于无穷大时函数的极限

如果在x→∞的过程中，对应的函数值f（x）无限接近于确定的数值A，那么A叫作函数f（x）当x→∞时的极限.因此有如下的定义：

定义2 设函数f（x）当∣x∣大于某一正数时有定义，如果存在常数A，对于任意给定的正数ε（不论多么小），总存在正数X，使得当x满足不等式：∣x∣＞X时，对应的函数值f（x）满足不等式

∣f（x）-A∣＜ε

那么常数A就叫作函数f（x）当x→∞时的极限，记为

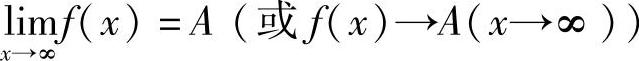
定义2 可简单表述为

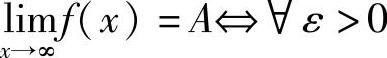，∃X＞0，当x＞X时，有∣f（x）-A∣＜ε

同理有x→+∞，x→-∞，f（x）的极限为A的定义：

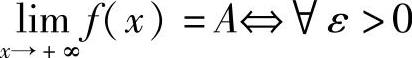，∃X＞0，当x＞X时，有∣f（x）-A∣＜ε；

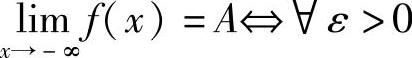，∃X＞0，当x＜-X时，有∣f（x）-A∣＜ε；

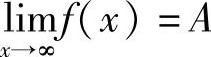的几何解释请学生思考.

例6 证明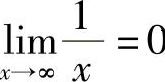：0.

证明 ∀ε＞0，要使

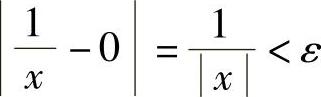
即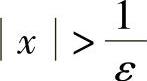只需要取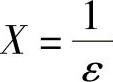，则当∣x∣＞X时，有不等式

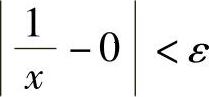
故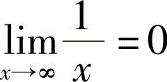

实际上，由几何意义可知y=0是函数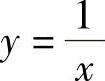的图像的水平渐近线.

一般地，如果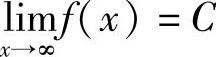，则直线y=C是函数y=f（x）的图像的水平渐近线.