为了以后计算及应用方便,首先进行如下补充规定:
(1)当a=b时,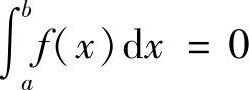 ;
;
(2)当a>b时,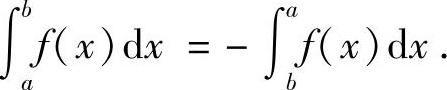
由补充规定(2)可知,交换定积分上、下限时,绝对值不变而符号相反.
假设下列性质中所列出的定积分都是存在的,则
性质1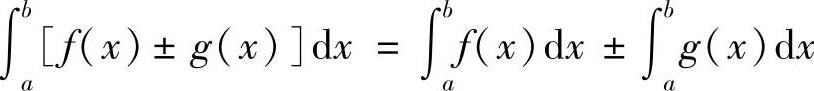
证明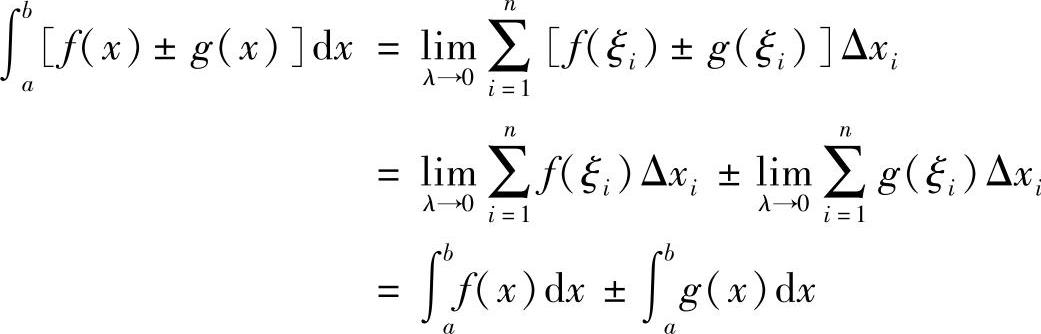
此性质可以推广到有限多个函数求和的情况.
性质2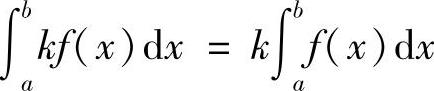 (k是常数)
(k是常数)
证明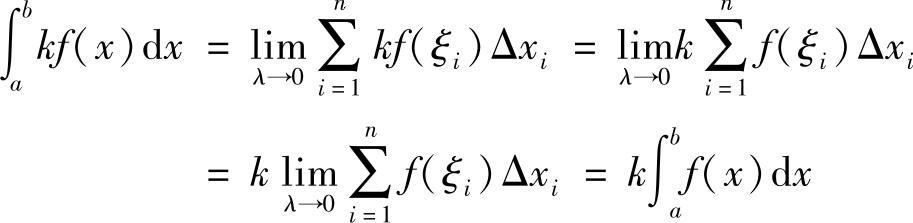
性质3 设a<c<b,则
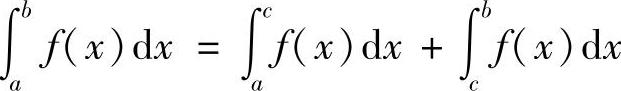
这个性质表明定积分对积分区间具有可加性,而且不论a,c,b的相对位置如何,此等式总是成立的.
性质4 如果在区间[a,b]上f(x)≡1,则
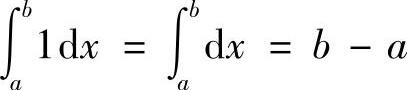
性质5 如果在区间[a,b]上f(x)≥0,则
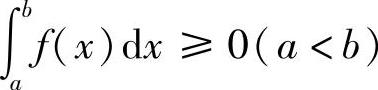
证明 由f(ξi)≥0(i=1,2,…,n),Δxi≥0,则
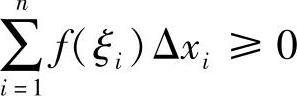
又λ=max{Δx1,Δx2,…,Δxn},则由极限的保号性有
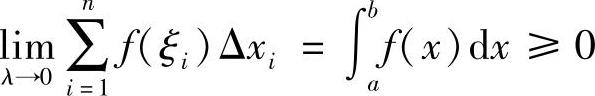
推论1 如果在区间[a,b]上有f(x)≤g(x),则
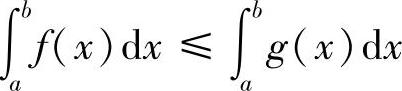
证明 由g(x)-f(x)≥0,得
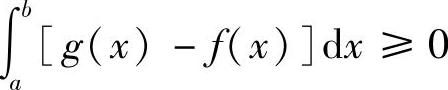
即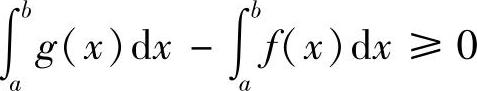
所以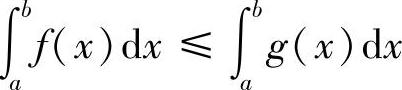
推论2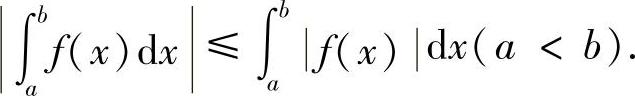
证明 由于-f(x)≤f(x)≤f(x),则
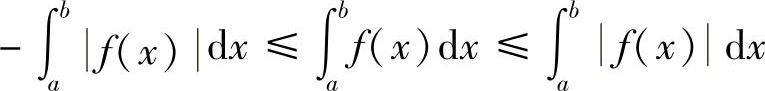 (https://www.xing528.com)
(https://www.xing528.com)
即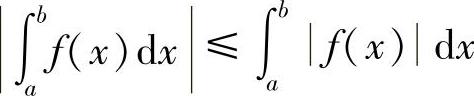
性质6 (估值不等式)设M及m分别是函数f(x)在区间[a,b]上的最大值及最小值,则
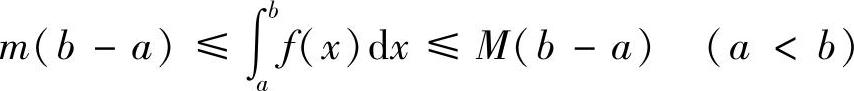
证明 由于m≤f(x)≤M,则
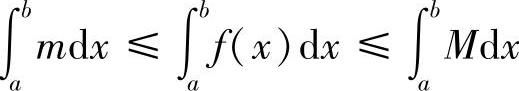
即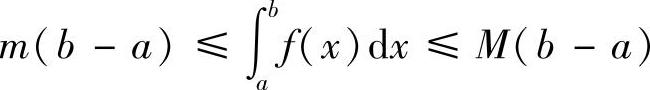
据此性质,利用被积函数在积分区间上的最大值及最小值,可以估计积分值的大致范围.
性质7 (积分中值定理)如果函数f(x)在闭区间[a,b]上连续,则在积分区间[a,b]上至少存在一点ξ,使
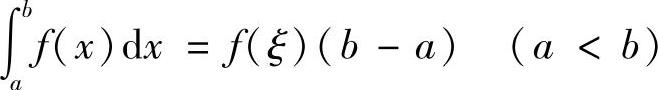
成立.这个公式叫作积分中值公式.
证明 由
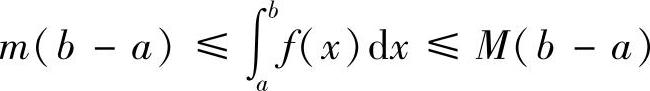
,得
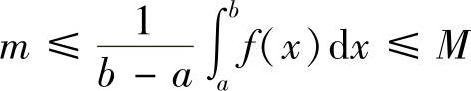
由介值定理知,在区间[a,b]上至少存在一个点ξ,使
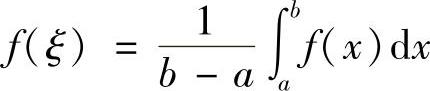
即
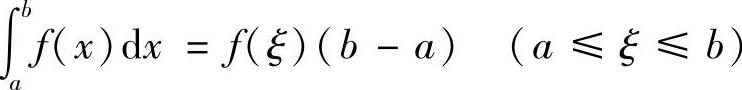
积分中值公式的几何解释:在区间[a,b]上至少存在一点ξ,使得以区间[a,b]为底边、曲线y=f(x)为曲边的曲边梯形的面积等于同一底边而高为f(ξ)的一个矩形的面积(见图5-2).
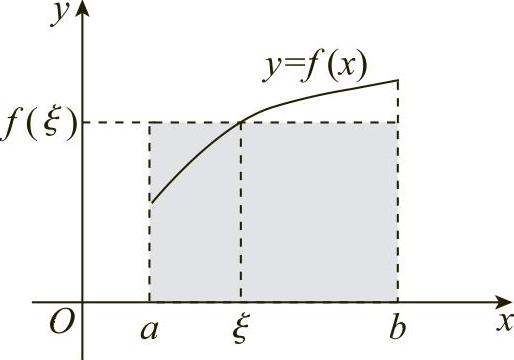
图5-2
例1 利用定积分的几何意义,求定积分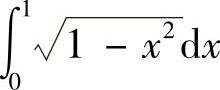 的值.
的值.
解 定积分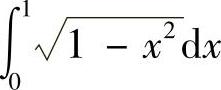 表示介于x=0,x=1,y=0,
表示介于x=0,x=1,y=0,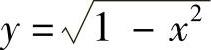 之间的面积,则
之间的面积,则
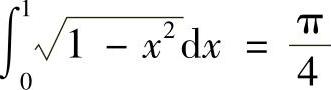
例2 证明: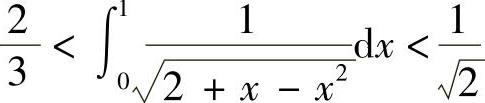 .
.
证明 因为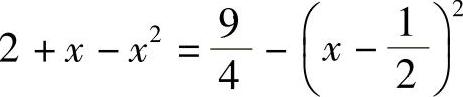 在区间[0,1]上的最大值为
在区间[0,1]上的最大值为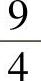 ,最小值为2,则
,最小值为2,则
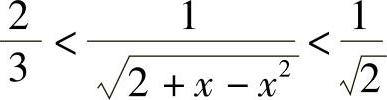
由积分估值不等式有
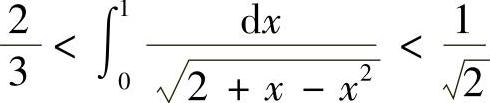
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




