局部线性嵌入(LLE)-高维数据流形学习分析方法

2.4.4.1　基本思想

LLE的基本思想是在任意一个样本点和它的邻域点之间构造局部线性平面，该样本点可以由它的邻域点线性重构而成，而且重构权值使得样本点与邻域点的线性重构误差达到最小。然后在低维空间中保持每个样本点与其邻域点的重构关系不变，并且假设低维空间的嵌入是局部线性的，通过最小化重构误差，可以得到高维向量在低维空间的嵌入结果。LLE中的最小重构误差权值能保持数据局部邻域的几何性质，即最小重构误差对于数据的平移、旋转和缩放是保持不变的。

2.4.4.2　算法步骤

(1)选择近邻点

在LLE算法中寻找近邻点的最简单的标准就是k近邻标准，以欧氏距离作为测度，来寻找离样本点距离最小的k个点作为其近邻点。另外还有其他一些标准也可以用来决定样本点之间的近邻关系，例如超球标准，即任意一个落在以样本点为球心、以ε为半径的超球内的点都可以看做近邻点。从以上两种标准可以看出，k近邻标准能够确定近邻点个数，而超球标准所确定的近邻点的个数是未知的(详见图2-4)。

(2)计算基于最小重构误差权值

图2-4　LLE的算法示意图

LLE算法的第二步就是对每一个样本点都由其近邻点进行线性重构。最小线性重构权值可通过以下表达式来计算:

其中，Wij是线性重构权值，Gjk是一个局部格莱姆矩阵。

式(2.12)是一个求解最小值的优化问题，并且要满足如下的稀疏约束条件约束和重构权值和为1条件:

所以式(2.12)可以改写为如下的约束目标函数:

(www.xing528.com)

求解此约束最小值问题可以采用拉格朗日数乘法。由于Gjk是正定的，所以其逆矩阵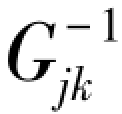是存在的，最优重构权值可以通过如下表达式来计算:

(3)特征映射

LLE算法的最后一步是根据第二步得到的最优权值矩阵W来计算输入样本的低维嵌入Y，可以通过如下表达式来计算:

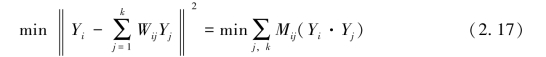
其中，Mij是一个n×n矩阵，定义如下:

式(2.17)是一个求最小值的优化过程，而且还满足一些约束条件，包括消除平移自由度和旋转自由度约束表示如下:

所以，可以将式(2.17)改写成如下约束目标函数:

满足这些约束条件下的优化嵌入可以通过多种方法来求得。但是最直接和最简单的方法是求代价矩阵M的最小的d＋1个特征值所对应的特征向量。注意到最小特征值所对应的特征向量是一个全1向量，它表示的是特征值为0所对应的自由平移模式，所以必须去掉这个向量，剩下的d个特征向量组成了经过LLE算法映射后的嵌入。

2.4.4.3　算法分析

LLE算法可以学习具有局部线性结构的任意维低维流形。它以重构权值矩阵作为高维观测空间与低维嵌入空间之间联系的桥梁，使得数据点与其近邻点在平移、旋转和缩放等变化下保持近邻关系不变。而且LLE算法具有解析的全局最优解，无需迭代。在算法的计算复杂度上，选择邻域的计算复杂度为O(Dn2)，计算重构权值矩阵的计算复杂度为O(Dnk3)，求解低维嵌入Y的计算复杂度为O(dn2)，如果采用一些专门针对稀疏、对称矩阵的特征值分解的方法可以使LLE算法中计算特征映射的计算复杂度降低到O(n2)。与ISOMAP和MVU算法相比，LLE算法的计算复杂度要小得多。但LLE算法也存在一些缺点:①由于LLE算法只是保持局部近邻的重构权值关系，并不是保持距离关系，因此，LLE算法不能很好地恢复出具有等距性质的流形；②LLE算法希望位从低维流形上的样本集中均匀稠密采样，因此，对于受噪声污染、样本密度稀疏或相互关联较弱的数据集，在从高维观测空间到低维嵌入空间的映射过程中，可能会将相互关联较弱的奇异点映射到局部近邻点的位置，从而破坏了低维嵌入结果。