功率谱及其在滤波中的应用

当我们进行图像处理时，有时可以通过计算图像之间的相关来获取一些有用信息。例如，当我们讨论两张图像的亮度模式之间的相似性时，图像之间的相关为我们提供了一个度量标准，如图9.6所示。函数a(x,y)和b(x,y)的互相关的定义为：

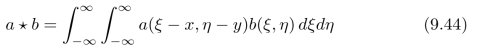
我们用ϕab(x,y)来表示式(9.44)中的积分，也就是说，ϕab=a★b。

注意，互相关和卷积

的定义很相似，它们之间唯一的区别在于：被积表达式中的第一个函数的形式。对于互相关，函数a(x,y)在和b(x,y)相乘之前，先被平移了(x,y)；而在卷积中，第一个函数a(x,y)除了平移以外，还要沿着x轴和y轴进行翻转。

我们在图像处理中常常使用的基于“滑动窗口”的相关操作，事实上是在计算相关而并非卷积。只是由于我们常常选用具有对称性的模板（或滑动窗口），使得相关和卷积的计算结果一致，我们才“习惯性地”将这些操作“称为”卷积。

如果a(x,y)=b(x,y)，那么，式(9.44)的结果被称为自相关。一个函数的自相关是对称的，也就是说，ϕaa(x,y)=ϕaa(x,y)。注意：任意函数的自相关都在(x,y)=(0,0)处取得最大值。根据Cauchy-Schw arz不等式，

其中，a(x,y)和b(x,y)是两个实函数，‖a(x,y)‖2是a(x,y)的L2范数，也就是说，。当且仅当a(x,y)=k·b(x,y)时（其中k为常数），等号才成立。因此，对于任意的(x,y)，都有：

如果b(x,y)是由a(x,y)经过移动后形成的，即：

(www.xing528.com)

图9.6　相关可以用于：对两张相似图像a(x,y)和b(x,y)进行比较；此外，它还可以被用于判断：由某种已知模式所组成的图像“片段”在图像中的位置。

那么，a(x,y)和b(x,y)的互相关将在经过一个合适的移动(x0,y0)后，取得最大值，也就是说，对于任意的(x,y)，我们都有：注意：可能存在其他的最大值点，特别是当a(x,y)为周期函数时。但是无论如何，如果b(x,y)可以被近似看作是：由a(x,y)经过移动而形成的，那么，我们可以通过计算ϕ(a,b)，来对移动量进行估计。

通常，互相关和自相关的Fourier变换是很重要的。它们被称为功率谱，分别记为：Φa,b(p,q)和Φa,a(p,q)。如果函数a(x,y)的Fourier变换为A(p,q)，那么，

其中A*(p,q)表示A(p,q)的共轭。因此，Φaa(p,q)总是一个非负实数。根据如下两个性质：1)ϕaa的对称性，以及，2)a(x,y)的Fou rier变换为A*(p,q)，我们可以直接得出式(9.50)中的结论。

对于很小的δu和δv，下式：

表示的是：频率域上u到u+δu和v到v+δv之间的长方形区域内的功率。这正是“功率谱”这个术语的原始意义。

一个有趣的例子是随机噪声。如果在一张图像中，每一个点的值都是：一个均值为0、标准差为σ的随机噪声，那么，这张图像的Fou rier变换是：一张和原图非常相似的随机图像^[1]，其均值为0，标准差为2πσ。对无数张这样的随机图像取平均，在所得到的结果的功率谱中，所有频率分量的值都会趋近于常数(2πσ)2。

图9.7　最优滤波器是使得输出结果o(x,y)与所希望得到的信号d(x,y)的“差别”最小的滤波器。将信号b(x,y)加上噪声n(x,y)以后，输入一个无限冲击响应为h(x,y)的线性移不变系统后，得到了滤波器的输出结果o(x,y)。