空穴膨胀理论的解析与应用

空穴膨胀理论是分析侵彻问题的重要理论方法。空穴膨胀理论假设弹体侵入部分在介质中以恒定速度扩展出球形（球形空穴膨胀模型，Spherical Cavity Expansion）或者柱形（柱形空穴膨胀模型，Cylindrical Cavity Expansion）空穴，扩展速度沿介质与弹体接触点法向。按照以上假定，通过求解介质中动力方程和空穴运动方程，可获得侵彻过程中不同物理参量。

基于空穴膨胀理论，空穴区域分为三个部分：锁变弹性区、锁变塑性区、无应力区或自由区，如图2.7所示。在锁变弹性区中，应力-应变满足弹性关系，但体积膨胀应变ϵ为常量ϵE。在锁变塑性区中，应力-应变满足理想的强化塑性本构关系，但体积膨胀应变ϵ为一常量ϵP，且有ϵP＞ϵE。按照动力理论，在弹性区，材料密度不变，为ρE；在塑性区中，密度也不变，为ρP，且ρP＞ρE。球形或柱形空腔区域在几何上均呈现球对称或轴对称。

球形空穴膨胀过程中，在锁变弹性区内

在锁变塑性区内

图2.7　空穴区域划分

式中，λ、G为拉梅常数；ϵE和ϵP分别为弹性区和塑性区的体积变形常数；下标r代表球面坐标系轴向方向，下标θ代表球面坐标系径向方向。

侵彻过程中，球形弹体所受压力，分为静压pS和动压pD两部分，且有

式中，r为欧拉径向坐标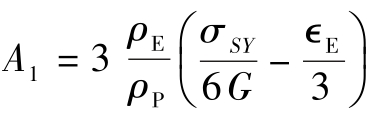；，其中σSY为材料常数；EP为线性强化塑性域的切变模量。

球形空穴膨胀的运动和球形弹体向前侵入的运动不同，球面膨胀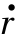速度和加速度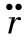均与球面垂直，且在球面上均匀分布。球面上动力压强为pD，如图2.8（a）所示。动力压强在向前半球面上的合力为

对侵入的运动弹体而言，球面上各点运动都不垂直于球面。因此，球面上各点动力压强也不是均布的。研究中假设球面上各点动力压强按cosθ规律分布，最大值在球面顶点。各点动力压强为，其中为球面顶点动力压强值。将代入式（2.38），得

式中，z为沿侵入方向延长的直线坐标。

图2.8　膨胀空穴和侵入球体压强分布

此时侵入阻力表述为

对于静压pS而言，两者相同，合力为

此时，球形弹体运动方程可表述为

式中，m为弹体质量。为使弹体运动方程更易于积分，将z z˙˙改写为改写为v0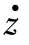，则式（2.45）变成线性微分方程

积分条件为

弹体运动的线性微分方程表述为(www.xing528.com)

其中，

结合积分条件，弹体运动线性微分方程的解为

求弹丸侵入深度P的边界条件为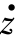=0，则

因此，弹丸侵入深度为

代入λ、Q，侵入深度表述为

对式（2.46）精确积分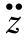，可表述为

此时，由式（2.52）和式（2.46）可得

满足初始积分条件的解为

侵深边界条件为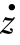=0，z=P，代入式（2.54）可得

在基本空穴膨胀理论的基础上，研究表明，弹体在侵彻过程中的轴向力，一部分来源于径向力σr，另一部分来源于剪应力σs。则弹体运动方程为

式中，系数来自σs的有效轴向分量σssinθ在球面上的积分，即

对于不同弹头，σr、σs分别为

式中，σr（ce）、σθ（ce）为空腔膨胀理论（考虑压缩性）的σr和σθ；α为弹头形状修正系数；ψ为彼斯脱数。对于锥形弹体而言

对于卵形弹头

式中，L为弹体总长；LN为弹头长；r0为弹体半径。彼斯脱数ψ为

根据可压缩空穴膨胀理论，σr（ce）、σθ（ce）为

式中，α（ch）为亲和应力；ξF为内摩阻角；I为刚性标数。