改进刚体极限平衡法

用有限单元法计算楔形体的稳定性是可行的途径，其计算精度高，比较符合楔形体变形和破坏的真实情况。但有限单元法的数据准备、输入、成果整理等工作量大，不如刚体极限平衡法简便。目前楔形体稳定分析所采用的刚体极限平衡法又因采用了法向分解假定和无矩假定，使得误差较大且偏于不安全。因此，笔者（陈胜宏，1990）考虑发展一种新的分析方法，使其既简便又有较高的精度。

有限单元法分析的结果，揭示了滑动面上应力状态的主要影响因素除强度参数外，还有滑动面的几何特性与变形特性，而楔形体和围岩的变形及强度参数的影响则很小。据此，可以把楔形体和围岩作为刚体，仅考虑滑动面的变形及强度特性，利用楔形体的力与力矩平衡方程、楔形体形心位移与滑动面变形的几何相容条件、滑动面的弹粘塑性本构方程来建立求解楔形体变形与稳定的基本方程。

一、坐标系、坐标变换及力学量记号约定

为推导方便，建立如下整体坐标系：X轴水平向北，Y轴水平向西，Z轴铅直向上，整体坐标用（X，Y，Z）表示。

图2-2-2　滑动面上的局部坐标系

每个滑动面都有一套局部坐标系：x j轴和y j轴在第j个滑动面上，且x j轴指向滑动方向，z j轴则与滑动面垂直且指向楔形体外部。局部坐标系的原点在滑动面的形心，其整体坐标为（X 0j，Y 0j，Z 0j）。楔形体形心的整体坐标则为（X 0，Y 0，Z 0）。

定义从整体坐标系到局部坐标系的变换为

二、基本方程的建立

1.楔形体的力与力矩平衡方程

对两滑动面上的应力进行积分，并向楔形体的形心简化，可在整体坐标系中写出楔形体的平衡方程为

式中：[P 1]j、[P 2]j是滑动面上积分点的局部坐标、滑动面形心整体坐标和楔形体形心整体坐标的函数。

2.楔形体形心位移与滑动面变形的几何相容方程

若楔形体形心发生位移增量{ΔU}，则在滑动面两侧的岩体将引起相对位移{Δu}j，应用运动学原理可推出两者的关系为

式中：[M]j为3×6阶矩阵，其元素为滑动面上积分点的局部坐标、滑动面形心整体坐标和楔形体形心整体坐标的函数。

3.滑动面的弹粘塑性本构方程

取滑动面的屈服函数为

(www.xing528.com)

式中：φ、c和σT分别为滑动面的摩擦角、凝聚力和抗拉强度。

滑动面的弹粘塑性本构方程可写为

弹性矩阵可由滑动面的法向和切向刚度系数k n和k s表达为

三、基本方程的求解

将相容方程（2-2-10）和本构方程（2-2-12）代入平衡方程（2-2-8），可得到关于楔形体形心位移增量{ΔU}的方程

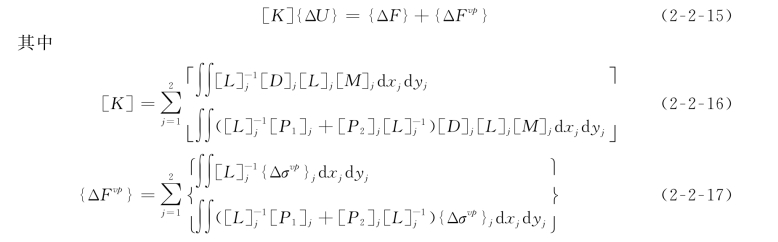
在任何时间步，首先由式（2-2-15）解出楔形体形心位移增量{ΔU}，然后用式（2-2-10）计算滑动面j上的相对位移增量{Δu}j，接着用式（2-2-12）计算滑动面j上的应力增量{Δσ}j，从式（2-2-13）和式（2-2-17）求出粘塑性应力增量{Δσvp}j和等效荷载增量{ΔF vp}后，即转入下一时步的重复计算。若滑动面的强度降到一定值时，以上计算发散，则说明楔形体已不能维持平衡，据此即得出安全系数。

四、算例

某楔形体（图2-2-1）的计算参数如表2-2-1～表2-2-3所示。

表2-2-1　几何参数

表2-2-2　滑动面的力学参数

表2-2-3　岩石的力学参数

图2-2-3给出了弹塑性有限单元法（FEM）、改进弹粘塑性法（IM）、刚体极限平衡法（LEM）、分块法（PM）等4种方法计算的强度储备安全系数。可以看出，改进弹粘塑性法的结果与弹塑性有限单元法的结果接近，刚体极限平衡法和分块法分别给出了安全系数的上、下限，当刚度比R=k n/ks增大时，改进弹粘塑性法的结果和有限单元法的结果都向上限靠近。

图2-2-3　楔形体的安全系数