自由振动中的粘性阻尼现象

如图1.9所示为有粘性阻尼的单自由度振动模型。质量为m的机器用橡胶垫做隔振处理，就可用此模型近似表示。图中的活塞符号表示粘性阻尼（Dash-pot）。由受力分析，容易推出该系统的运动方程式为

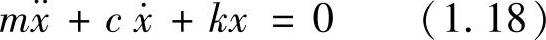
该方程的特解并不显而易见。这里，令x=e^λt，λ为常数。代入方程式（1.18），可求得

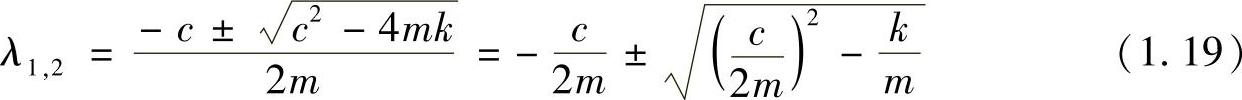
因此，可得两个特解e^λ1t，e^λ2t。于是，该方程的通解为

其中，C₁、C₂为两个由初始条件确定的常数。

这个解随着粘性阻尼c的不同取值而有着不同的特性。式（1.19）根号下的值为0时的阻尼定义为临界阻尼

引入阻尼比

可见，临界阻尼对应于ζ=1。而当ζ＞1时，称为过阻尼；当ζ＜1时，称为欠阻尼。

引入以上参数定义，式（1.19）可以重新写成

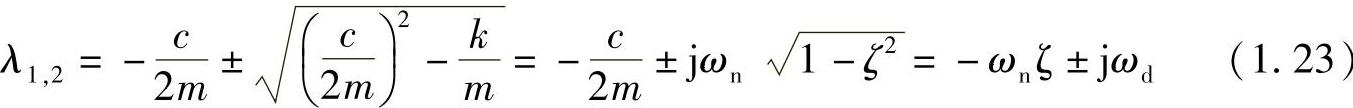
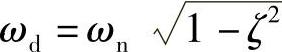称为有阻尼固有角频率。显然，对于欠阻尼的情况，该式才有意义。

以下来考查不同情况下通解（1.20）的特点。

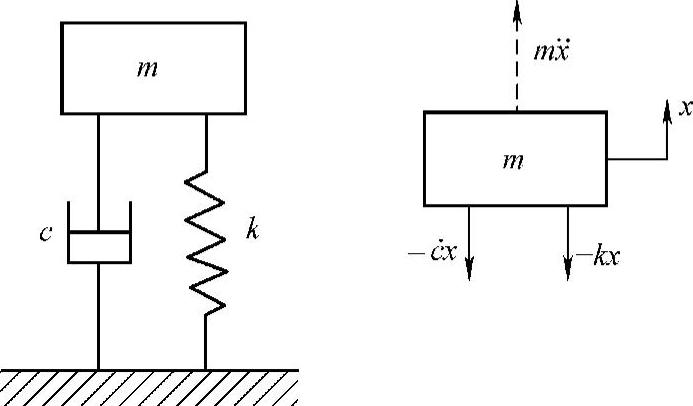
图1.9 有粘性阻尼的单自由度振动模型

1.临界阻尼的情况（ζ=1）

由于λ_1，2=-c/2m=-ω_nζ，特解为两个重根，通解为

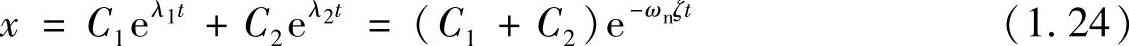
显而易见，这是一个指数衰减函数，表示初始状态的位移将随着时间的增加而单调地衰减至0。例如把物体从平衡位置拉开然后释放，物体将缓慢地返回原位而停止下来，不发生振动。

2.过阻尼的情况（ζ＞1）

这时式（1.23）成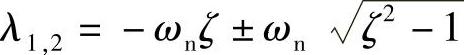为，通解为

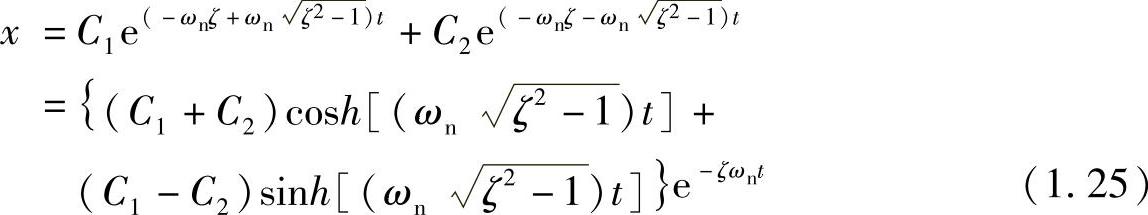
在式（1.25）的演变中，用到了双曲函数定理e±θ=cosh（θ）±sinh（θ）。这也是一个随时间增加而单调衰减的函数，振动现象不会发生。

假设如图1.9所示系统的无阻尼固有频率为2Hz，初始条件为x（0）=x₀，x·（0）=0。将这些初始条件代入公式（1.20）及其微分，可求得两个积分常数为

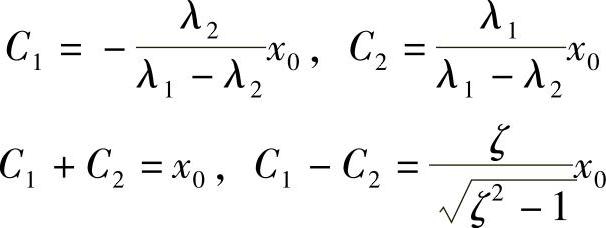(www.xing528.com)

这里取x₀=1mm，则对于ζ=1.0（临界阻尼）与ζ=1.1（过阻尼）两种情况，系统的位移如图1.10所示。由图可见，过阻尼时，物体返回原位的过程更缓慢。

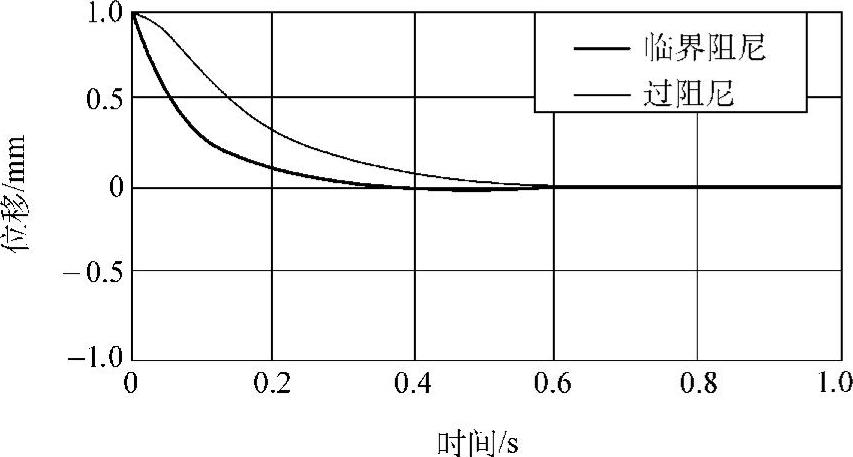
图1.10 临界阻尼和过阻尼情况下的系统响应

3.欠阻尼的情况（ζ＜1）

此时，将式（1.23）代入式（1.20），可得

在上述公式演变中，用到了欧拉公式e^±jθ=cosθ±jsinθ。这里，C′₁=C₁+C₂，C₂′=j（C₁-C₂）。

如果已知初始位移为x₀，初始速度为v₀，则可以推导出C′₁=x₀，C₂′=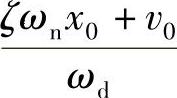，代入式（1.26）并变形可得

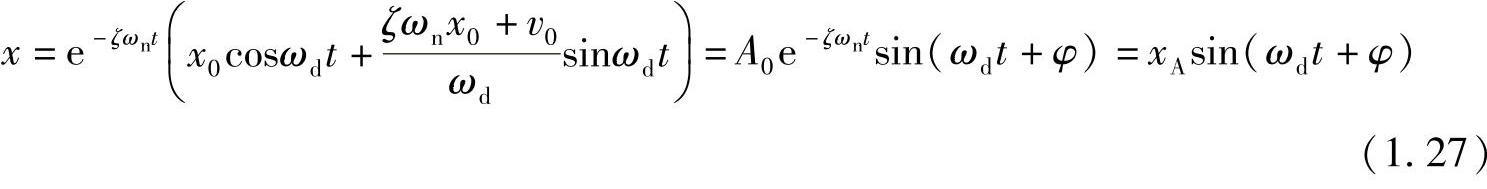
这里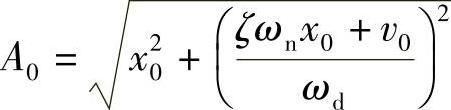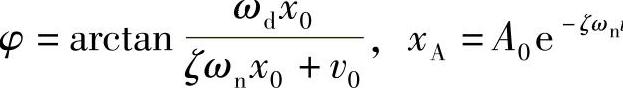，，t。

可见，这是一个有着正弦函数特性的振动解，其振幅x_A是一个指数衰减函数。

如图1.11所示为在相同的初始条件下（x₀=1，v₀=0），ζ=0.05以及ζ=0.2时的自由振动响应曲线（作为对比，图中细线表示临界阻尼的情况）。阻尼越大，振幅衰减得越快，同时，振动周期稍微变长。

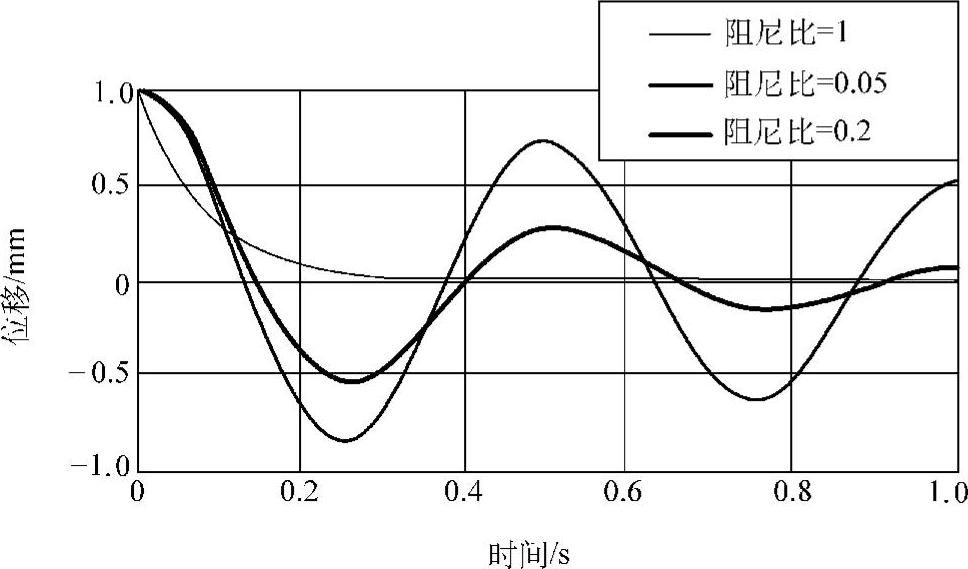
图1.11 欠阻尼情况的自由振动

这里，对自由振动的衰减特性做一考察。在给定阻尼的情况下，自由振动的周期一定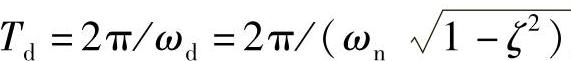，。每经过一个周期，振幅都会变小（参见图1.12）。在每个峰值处，式（1.27）中的正弦函数的值为1，于是，峰值的大小可以表示为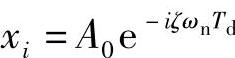，i=0，1，2，3，…。因此，第（i+1）个峰值与第i个峰值之比为。这是一个小于1的常数，它说明粘性阻尼系统的自由振动的振幅依照等比级数的规律衰减。这里，定义对数衰减率（Logarithmic Decrement）为δ=ln（x_i/x_i+1），则有下列关系

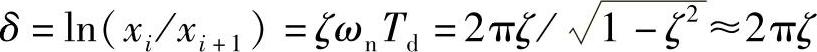
可见，对数衰减率大约是阻尼比的6倍。尽管在大多数情况下，阻尼比远小于1，但对数衰减率却可能大于1。例如对于汽车减振器，一般δ=2。

测量到对数衰减率，由上式可以得到阻尼比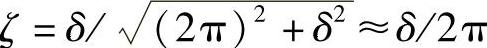，这是确定系统阻尼比的简单方法。当阻尼很小时（δ<<1），对数衰减率可由以下更简便的方法得到：

由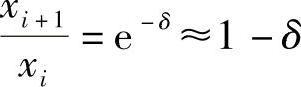推算得

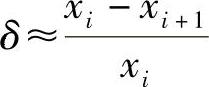
作为参考，表1.1列出一些材料及结构的阻尼比的常见值。

表1.1 常见材料或结构的阻尼比ζ（仅作参考）

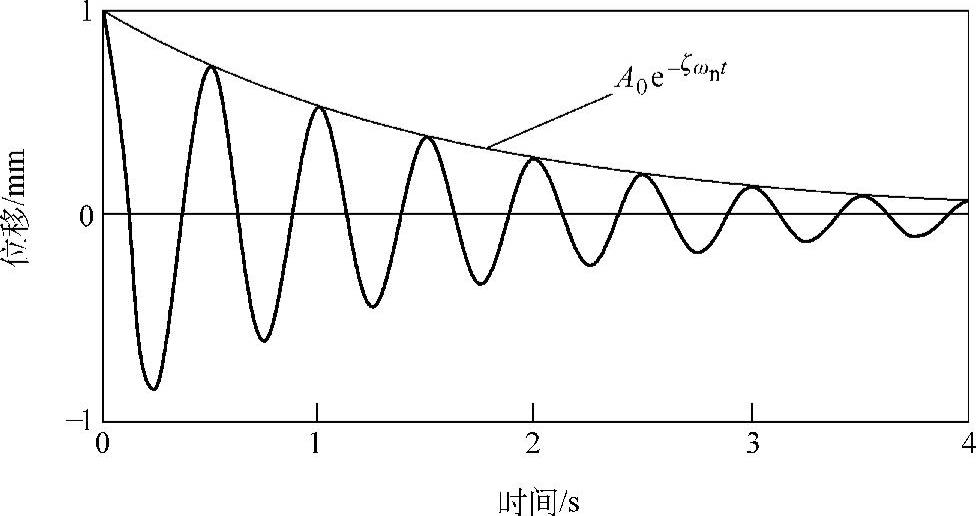
图1.12 自由振动的衰减率

式（1.27）中的指数函数描述了自由振动响应的衰减特性（参见图1.12）。影响自由振动衰减特性的参数有两个：一个是阻尼比ζ，一个是自由振动角频率ω_n（固有角频率）。阻尼比越大，振动衰减得越快；在阻尼比不变的情况下，固有频率越大，振动衰减得越快。在此，把二者之积定义为衰减指数σ=ζω_n（单位：rad/s），则用σ一个量即可客观地衡量衰减的程度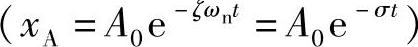。σ越大，振动衰减得越快。

实际结构的自由振动响应虽不像单自由度系统那样单纯，有时也可以用一个等价的衰减指数来衡量阻尼的大小。如图1.13所示为某薄板结构在阻尼处理前后的冲击响应（Impulse Response）。图中的指数衰减曲线是根据最小二乘法对测量结果的包络线作线性回归分析（lnx_A=lnA₀-σt）得到的。阻尼处理前，σ=2.4rad/s；处理后，σ=11.7rad/s。可见，用σ可以定量地评价阻尼处理的效果。