随机减量法和Prony方法的优化应用

随机减量法（Random Decrement Technique，简称RDT）是为进行结构模态参数时域识别所进行的预处理过程，以单自由度为例说明采用随机减量技术由结构随机振动响应数据获得结构自由振动响应数据的方法。任意激励下测点的受迫振动响应可表示为：

式中：D（t）是初始位移为1、初始速度为0的系统自由振动响应；V（t）是初始位移为0、初始速度为1的系统自由振动响应；y（0）、˙y（t）分别为系统振动初始位移和初始速度；h（t）是结构单位脉冲响应函数；f（t）是外部激励。

选取一个适当的振幅A去截取一个结构实测随机振动响应信号，可得到一系列交点ti（i=1，2，3，…，n）。对于自ti时刻开始的响应y（t-ti），可以表示为：

将式（14.2）的时间起始点ti移至坐标原点，可获得一系列随机过程的子样本函数x i（t）（i=1，2，3，…，n）：

取x i（t）的统计平均：

由于激励f（t）是均值为0的平稳正态过程，E[f（t）]=0，且y（t）、˙y（t）也是均值为0的平稳正态过程，则˙y（ti）是均值为0的随机变量，E[˙y（ti）]=0。故

由此获得了某一测点初始位移为A、初始速度为0的自由振动响应，然后采用Prony法去识别结构的模态参数。该方法是根据结构的自由振动响应可以表示为复指数函数和的形式，在求解过程中构造了Prony多项式，然后用线性方法确定未知参数。

将tk=kΔt时刻的结构自由振动反应表示为：

为了求振型，令式（14.6）中的k=0，1，2，…，M-1，此时Zi已知，则由M个线性方程，可解得M个未知数φri（i=1，2，3，…，M）。

14.1.2 NEx T法

自然激励技术（Natural Excitation Technique）简称NEx T法的基本思想是：白噪声环境激励下结构两点之间响应的互相关函数和脉冲响应函数有相似的表达式，求得两点之间响应的互相关函数后，再运用时域模态识别方法进行模态参数识别。其基本原理如下。

对于自由度为N的线性系统，当系统的k点受到力f k（t）的激励，系统i点的响应x ik（t）可为：

式中：φir为第i测点的第r阶模态振型；akr为仅同激励点k和模态阶次r有关的常数项。

当系统的k点受到单位脉冲力激励时，就得到系统i点的脉冲响应h ik（t），可表示为：

对系统k点输入力f k（t）进行激励，系统i点和j点测试得到的响应分别为x ik（t）和x jk（t），这两个响应的互相关函数的表达式为：

假定激励f（t）是理想白噪声，根据相关函数的定义，则有

式中：δ（·）为脉冲函数；ak为仅同激励点k有关的常数项。

将式（14.17）代入式（14.16）并积分，得到：

对式（14.18）的积分部分进行计算并化简，可得：

bjr仅为同参考点j和阶次r有关的常数项。

比较式（14.15）和式（14.19），线性系统在白噪声激励下两点的响应的互相关函数和脉冲激励下的脉冲响应函数的数学表达式是完全一致的，互相关函数确实可以表征为一系列复指数的叠加的形式。互相关函数具有和系统的脉冲响应函数同样的性质。因此互相关函数可以用于基于时域的模态参数识别中，用来代替脉冲响应函数。

14.1.3 奇异熵定阶降噪的ERA方法

特征系统实现算法（ERA）利用实测脉冲响应或自由振动响应数据，通过Hankel矩阵及奇异值分解，寻找系统的一个最小实现，并将该实现变换为特征值规范型。因此，在系统最小实现理论的基础上发展起来的特征系统实现算法，可用于脉冲激励下或结构自由衰减的时域模态参数识别，该算法只需响应数据，识别所需数据短、速度快，能得到系统的最小实现，便于控制应用，与其他时域方法相比，该方法有最佳的精度，是目前结构环境振动模态参数识别最先进的方法之一[3]。结构振动的状态方程在线性离散空间内可表达为：

式中：k为采样点序号；x（k）为在kΔ时刻系统的状态向量；Δ为采样时间间隔；u（k）为输入向量；y（k）为输出向量；A、B、C分别为系统矩阵、控制矩阵和输出矩阵。

在kΔ时刻，由各测量点的脉冲响应可构成系统脉冲响应函数矩阵h（k）={hij（k）}，其中hij（k）为k时刻激励点和响应点j之间的脉冲响应函数值，常数矩阵h（k）称为马可夫（Markov）参数矩阵。经典的Hankel矩阵由Markov参数矩阵按下列形式构成：

对0阶Hankel矩阵H（0）进行奇异值（SVD）分解，得：(www.xing528.com)

其中，H（0）为（r+1）×（s+1）维实矩阵，P为（r+1）×l维正交矩阵，Q为（s+1）×l维正交矩阵，Dr=diag（d 1，d 2，…，dr），r=rank[H（k）]，（r＜l且di≠0，i=1，2，…，r）。设Pr、Qr分别为P、Q矩阵的前r列，则由系统最小实现论可得系统矩阵为：

对系统矩阵A进行特征值分解：

式中：Z为特征值矩阵；ψ为特征向量矩阵。

由振动理论和状态方程的解可求得：

式中：T为采样时间间隔；ωi、ζi分别为结构无阻尼角频率和阻尼比。由此可得：

时域系统识别时系统的阶次是一个最重要的参数，在特征系统实现法识别过程中，需要构造Hankel矩阵，并确定Hankel矩阵的阶次大小，同时系统矩阵A的阶次也需要确定，才能最终识别出系统的各项模态参数（频率、阻尼、振型）。环境激励下的结构模态参数识别，系统是未知的，真正的系统阶次究竟是多少，并不可能知道，只能用一个近似等于系统阶次的阶次来代替这个未知系统的阶次才可以开始计算，这个近似阶次所包含的对应特征信息应是尽量的多，以免丢失信息，这必将会引入噪声模态。针对结构系统定阶难的问题，本文引入熵的概念，提出利用奇异熵增量的变化首先对原始信号进行初步定阶、降噪与重构，利用奇异熵增量对H（0）（即脉冲响应构造的矩阵）进行进一步定阶与消噪，最后确定结构系统的真实工作模态阶数，也即系统矩阵A的阶次。

1.熵的定义

熵（Entropy）是由德国物理学家克劳修斯在1865年提出的，是应用范围非常广泛的一门学科理论，熵既是一个物理学概念，又是一个数学函数，也是一种自然法则。对于一个广义的系统来说，熵可作为系统状态的混乱性或无序性的度量。一般来说熵值越小，系统不稳定性、无序性和不确定性的程度就越小。目前，熵的应用已经远超出热力学和统计物理的概念，在信息学、数学、天体物理、生物医药等领域也有着广泛应用。熵是系统状态不确定性的一种度量，假设系统可能处于n种状态，处于每种状态的概率为p i（i=1，2，…，n），则系统的熵为[4]：

2.奇异熵与奇异谱

根据信号奇异值分解原理[5 6]，对于一个m×n维的实矩阵D，必然存在一个m×l维的矩阵R，一个l×l维的对角线矩阵Λ和一个n×l维的矩阵S，使得如下关系成立：

式中，对角元素矩阵Λ的主对角元素λi（i=1，2，…，l）是非负的，并按降序排列，即λ1≥λ2≥…≥λl≥0，这些对角元素便是矩阵D的奇异值。

当信号无噪声或具有较高信噪比时，对其进行奇异值分解后得到的Λ矩阵可以描述为：

而当信号具有较低信噪比时，其奇异值分解后得到的Λ矩阵可描述为：

显然，Λ矩阵中非零主对角线元素的多少与信号所含频率成分的复杂与否有着密切的联系。Λ矩阵中非零值主对角线元素越多，信号成分越复杂，甚至当信号受到噪声干扰后，Λ矩阵的主对角元素有可能均为非零值；而Λ矩阵中的非零值主对角元素越少，则说明信号的频率成分越简单。由此表明，Λ矩阵可对工程结构振动信号的信息量作出客观反映。基于Λ矩阵的特性，引入了信号奇异熵的概念，即信号的奇异熵定义式为：

式中：k为奇异熵的阶次；ΔEi为奇异熵在阶次i处的增量。可通过下式计算得到：

则由σi（i=1，2，…，l）组成的序列便为矩阵A经奇异值分解后得到的奇异谱。可见，信号的奇异熵值越大，说明信号越复杂，信号所含的信息也就越丰富。

3.基于奇异熵的信号降噪原理

假设一结构动力响应测试信号X，为对其进行降噪处理，利用延时嵌陷技术，将原始信号x（t）=[x（t）x（t+τ）x（t+2τ）x（t+3τ）…]（τ为延时）映射到m×n维相空间内，得到重构吸引子轨道矩阵D[7]：

将矩阵A进行奇异值分解，按式（14.23）～式（14.25）可求得信号的奇异熵及其增量。对于Λ矩阵中高阶次下的非零对角元素完全是因噪声干扰所致。因此若只保留奇异值矩阵Λ中的前k个主对角线元素，而将后（l-k+1）个主对角线元素均取为零，再将所得新主对角矩阵代回式（14.28），便可得到：

则通过式（14.34）计算出的矩阵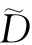便可认为是原轨道矩阵D的一个估计。于是根据重构吸引子轨道矩阵的重构原理，通过矩阵便可得到原信号X经降噪处理后的信号X～。由此看出，信号的奇异谱降噪实际上相当于对原信号进行了低通滤波处理：

式中，W表示一低通滤波器，其数学表达式为：

对于确定的信号重构吸引子轨道矩阵D，对其进行奇异值分解后，矩阵Λ和V是确定的。因此，通过公式（14.36）可知，低通滤波器W主要决定于矩阵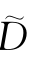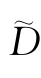，的构造直接决定着信号最终的降噪效果。

4.基于奇异熵的系统定阶

在对原始信号经奇异值分解降噪处理后，可利用NEx T法求得结构某点的系统脉冲响应，再利用ERA算法识别结构模态参数。ERA识别算法首先需要构造Hankel矩阵，求出系统矩阵A，对A进行奇异值分解可求得系统特征值。理论上系统的特征值个数为2N，虽然原始信号已进行降噪处理，但仍有部分噪声存在，此时对H（0）进行奇异值分解时，奇异值对角矩阵元素往往大于2N，单凭奇异值大小确定系统的阶次往往比较困难。通过比较H（0）和吸引子轨道矩阵D可以发现，H（0）的构造和D的构造形式完全相同，H（0）反映的信息是结构脉冲响应信息矩阵，D反映的是结构原始信号信息矩阵。因此，H（0）的定阶可用奇异熵理论来确定。通过计算H（0）经奇异值分解后的奇异谱和奇异熵增量，对于同一脉冲响应信号而言，无论信号受噪声干扰的严重程度如何，对其有效特征信息进行完整抽取所需的奇异谱阶次是一定的（也即系统的阶次是一定的）。选取奇异熵增量开始降低到渐近值时的阶次来作为系统结构定阶是非常合理的，可见，这一系统定阶过程是基于奇异熵消噪与定阶的两个过程同时进行，即对脉冲响应信号再一次进行了消噪，同时也确定了结构的阶次。