寻求简捷解法——构造几何和向量模型

许多代数形式具有几何图形的特征，许多几何问题通过构造辅助图形变为规则的几何图形之后，可以巧妙地解决这些问题，使所构造的图形更具操作性，将题设条件及数量关系直接在图形中展现，然后在构造的图形中寻求问题的结论.

向量集数与形于一体，它沟通了代数、几何与三角函数的内在联系，构造向量模型解题被称为数形结合的典范，应用非常广泛，平面向量可以用来求解解析几何中的许多问题，在解立体几何问题时，运用空间向量法，可以使解题过程简洁明快，避免了作辅助线、证明等烦琐过程，通过向量的加(减)法、向量的数量积计算等轻松求解.

例1　(1)已知a，b为正数，且a≠b，证明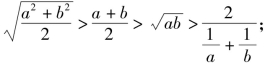

(2)对于正整数n，定义Sn为和式的最小值，其中a1，a2，…，an是正实数，它们的和是17，存在唯一的正整数n，使Sn也是一个正整数，求这个正整数n.

解题策略　第(1)问为二元基本不等式及其变形公式，用代数方法证明很简单，下面给出的是构造几何图形来证明，实质也是不等式的几何解释.第(2)问，形似勾股定理，故可以联想构造一系列的直角三角形来求解.

证明　由于

可先构造Rt△ABC,使得

此时斜边

再以为斜边，为直角边构造Rt△BCD.

则

最后，作Rt△BC′D≌Rt△BCD,过D作DE⊥BC′交BC′于E.

图2-7

如图2-7所示.

由图形直观得AB>BC>BD>BE,

即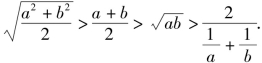

图2-8

(2)如图2-8所示，作AB1=1，C1B2=3，…，Cn-1Bn=2n-1;B1C1=a1,B2C2=a2,…，Bn-1Cn-1=an-1,BnC=an，那么

BC=a1+a2+…+an=17.

因为

所以n4+172=m2，n∈N*，即(m-n2)(m+n2)=289，

因为m+n2为正整数，且m+n2>m-n2，

所以m-n2=1，m+n2=289，所以n=12(舍去负根).

即当n=12时，S12=145.

例2　(1)已知正三棱锥P-ABC，点P，A，B，C都在半径为的球面上，若PA，PB，PC两两相互垂直，则球心到截面ABC的距离为________；

(2)若α，β，γ均为锐角，且满足sin2α+sin2β+sin2γ=1.

求证：

解题策略　第(1)问，利用补体方法，把正三棱锥扩展为棱长为2的正方体，以便于从整体上宏观把握，这种方法便是整体构造，目的在于从更广阔的范围内处理局部问题，是一种重要的解题方法.在本书数形结合的思想方法一章中，也会介绍过数形结合的桥梁——构造法，其中有一道例题是：已知α，β，γ均为锐角，且cos2α+cos2β+cos2γ=1.求证:其题设正是长方体的一个重要性质(读者可在本书相关章节中查阅).本例第(2)问正是上述这道例题的拓展,所不同的是上面所举的例题中,α，β，γ是长方体的体对角线与从一端点出发的三条棱所成的角，而本小题中的α，β，γ是长方体的体对角线与从一端点出发的三条面对角线所成的角,证明过程中除了运用二元基本不等式之外还需运用柯西不等式,这类题从三角函数角度证明极其烦琐,构造立体图形则证明过程简捷明快.

解：(1)依题意构造一个棱长为2的正方体,则正三棱锥P-ABC即为该正方体的一个角(从顶点P出发的3条棱分别为PA，PB，PC),且球心刚好就是以点P为一个端点的体对角线PQ的中点,易知平面ABC与PQ交于PQ的一个三等分点,且PQ⊥平面ABC,进而可得球心到截面ABC的距离

(2)证明　如图2-9所示，设a，b，c为长方体ABCD-A1B1C1D1的3条棱，其对角线AC1与3个面，即与面AC、面AD1、面AB1所成角分别为

图2-9

则

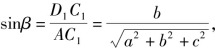
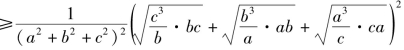
当且仅当a=b=c，即α=β=γ时取等号.

例3　(1)已知7sinα+24cosα=25，求tanα的值；

(2)求函数的最值；

(3)求函数的最小值；

(4)设x，y∈R+，且x+2y=10，求函数w=x2+y2的最小值；

(5)若实数x，y满足方程x2+y2-2x-4y+1=0，求代数式的取值范围.

解题策略　这一组题在其相应的知识范围内都是可以解决的，但是若构造向量，利用向量知识求解显得既简洁又巧妙.

对于(1)，在三角函数范围内可以有多种解法，运用向量运算则别具一格.(www.xing528.com)

对于(2)，变形后构造向量，利用即可求得函数最值，

对于(3)，在向量中有不少含不等式结构的式子，如： 对所给函数解析式通过构造向量，利用上述不等式求有关函数的最值.

对于(4)，设向量则与的数量积为：从而有：当且仅当与同向时取等号:得当且仅当与同向时取等号，上式结论可以推广到空间向量，读者可自行推导.

对于可以看作圆上一点P(x，y)与定点(-2,0)连线斜率，求斜率的范围，若构造向量，利用即可求得其取值范围.

解：(1)注意到系数满足72+242=252，可构造向量由可得即7=25sinα，24=25cosα，故

(2)由原函数解析式变形得2sinx+(3-y)cosx=4-2y，

构造向量

则解得

(3)所给函数为根式的和，通过对根号内的二次三项式配方，使之转化为向量的模，即原函数可化为

设

(4)设由定义有从而

当且仅当与同向，即时取等号，

∴当x=2，y=4时，w=x2+y2取得最小值20.

(5)设=k，则y=kx+2k　　①

∵方程x2+y2-2x-4y+1=0可化为(x-1)2+(y-2)2=4.

故可将①式写成-k·(x-1)+1·(y-2)=3k-2.

构造向量

则

由得(3k-2)2≤4(k2+1)，解得

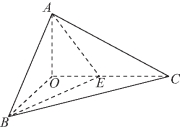
图2-10

故所求的取值范围是

例4　如图2-10所示，已知三棱锥O-ABC的侧棱OA，OB，OC两两垂直，且OA=1，OB=OC=2，E是OC的中点.

(1)求O点到面ABC的距离；

(2)求异面直线BE与AC所成的角；

(3)求二面角E-AB-C的大小.

解题策略　运用空间向量解立体几何问题，体现了“数”与“形”的结合，淡化了传统立体几何从“形”到“形”的推理方法，是构造法思想的体现，通过构造向量把立体几何问题转化到空间向量系统内求解，从而降低了思维难度，使问题变得程序化，这是用空间向量求解立体几何问题的独到之处，在建立恰当的空间直角坐标系的条件下，本题的解法归纳如下：

(1)点面距离：P为平面α外一点，分别为平面α的斜向量和法向量，d为P到α的距离，则

(2)异面直线的夹角：设两异面直线a、b所成角为分别是a、b的方向向量，注意到异面直线所成角的范围是则有

(3)二面角：设θ是两相交平面α、β所成的二面角(或其补角)，是平面α的一个法向量，是平面β的一个法向量，则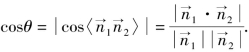

图2-11

解：(1)如图2-11所示，以O为原点，OB，OC，OA分别为x，y，z轴建立空间直角坐标系，则有A(0，0，1)，B(2，0，0)，C(0，2，0)，E(0，1，0)，设平面ABC的法向量为

则由知

由知

取

则点O到面ABC的距离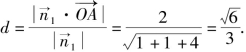

(2)

所以异面直线BE与AC所成的角为

(3)设平面EAB的法向量为

则由知

由知取

由(1)知平面ABC的法向量为

则

故二面角E-AB-C的大小为