高中数学：立体几何-高中数学高频考点例题精析

高考导航

1.关于立体几何，每年必考大题.第1问多为证明平行垂直问题，第2问多为计算问题，求空间角较多，其特点：证明过程中一般要用到初中平面几何的重要定理.

2.根据考查的角度不同，可以将考查分为两种类型：①直接考查，直接由题目所给关系判定平行、垂直关系或直接求角的大小；②逆向考查，即由给出平行、垂直关系或给出角的大小来判定点、线的位置，常以探索性问题出现.

例题精析

【例1】（2019年全国Ⅱ卷）如图5.1所示，长方体ABCD-A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.

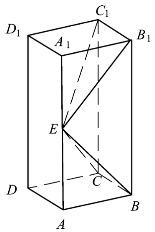
图5.1

（1）证明：BE⊥平面EB1C1.

（2）若AE＝A1E，求二面角B-EC-C1的正弦值.

▶　解题指南

（1）罗列条件（初审题）：①长方体ABCD-A1B1C1D1；②ABCD是正方形；③BE⊥EC1.

作分析图：

（2）几何法基本步骤：一作（难点）二证三计算.

几何法（难点——如何作二面角的平面角）突破思维流程：①有垂直于棱EC的面吗？如果有，用平面法作平面角；②半平面内有垂直于棱EC的线吗？如果有，用定义法作平面角；③有垂直于某半平面的线（或面）吗？如果有，用三垂线法作平面角（或射影面积法求）.

向量法（难点——如何建立空间直角坐标系）突破思维流程：①有没有两两垂直的三条棱？如果有，直接以这三条棱为坐标轴建系；②有没有线面垂直？如果有，则以垂足为原点建系；③有没有面面垂直？如果有，过面内一点作交线的垂线转化为②建系.

（3）规范书写解答过程.

▶　解析

（1）由已知得，B1C1⊥平面ABB1A1，BE⊂平面ABB1A1，故B1C1⊥BE.

又BE⊥EC1，所以BE⊥平面EB1C1.

（2）向量法（几何法略）：

由（1）知∠BEB1＝90°，由题设知Rt△ABE≌Rt△A1B1E，则∠AEB＝45°，故AE＝AB，AA1＝2AB.

以D为坐标原点，的方向为x轴正方向，为单位长，建立如图5.2所示的空间直角坐标系D-xyz，则

图5.2

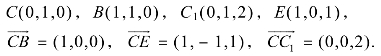
设平面EBC的法向量为n＝（x，y，x），则

变式1　1.如图5.3所示，在直四棱柱ABCD-A1B1C1D1中，底面ABCD是矩形，A1D与AD1交于点E，AA1＝AD＝2AB＝4.

图5.3

（1）证明：AE⊥平面ECD.

（2）求直线A1C与平面EAC所成角的正弦值.

▶　解析

（1）证明：因为四棱柱ABCD-A1B1C1D1是直四棱柱，所以AA1⊥平面ABCD，则AA1⊥CD.

又CD⊥AD，AA1∩AD＝A，所以CD⊥平面AA1D1D，则CD⊥AE.

因为AA1⊥AD，AA1＝AD，所以AA1D1D是正方形，则AE⊥ED.

又CD∩ED＝D，所以AE⊥平面ECD.

（2）因为四棱柱ABCD-A1B1C1D1是直四棱柱，底面ABCD是矩形，所以以A为坐标原点建立如图5.4所示的空间直角坐标系A-xyz，则

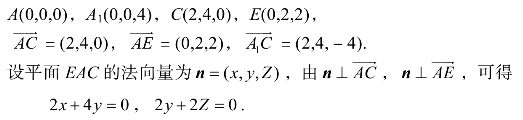
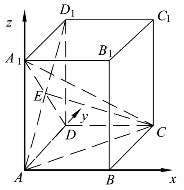
图5.4

令Z=1，则n=（2，-1，1），设直线A1C与平面EAC所成的角为α，则

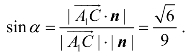
所以直线A1C与平面EAC所成角的正弦值为

2.如图5.5所示，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB＝2，∠BAD＝60°.

（1）求证：BD⊥平面PAC.

（2）若PA＝AB，求PB与AC所成角的余弦值.

（3）当平面PBC与平面PDC垂直时，求PA的长.

图5.5

规范解答

【例2】（2019年全国I卷）如图5.6所示，直四棱柱ABCD-A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，N分别是BC，BB1，A1D的中点.

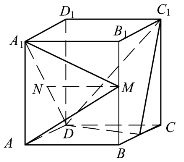
图5.6

（1）证明：MN∥平面C1DE.

（2）求二面角A－MA1－N的正弦值.

▶　解题指南

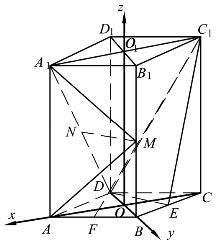
图5.7

变式2　1.如图5.8所示，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF∥AC，

（1）求证：AF∥平面BDE.

（2）求证：CF⊥平面BDE.

（3）求二面角A-BE-D的大小.

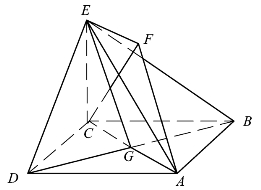
图5.8

▶　解析

（1）证明：设AC与BD交于点G.

因为EF∥AG，且EF＝1，AC＝2，AG＝1，

所以四边形AGEF为平行四边形，则AF∥EG.

因为EG⊂平面BDE，AF⊄平面BDE，

所以AF∥平面BDE.

（2）证明：因为正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，

所以CE⊥平面ABCD.

如图5.9所示，以C为原点，建立空间直角坐标系C-xyz，则

图5.9

2.如图5.10所示，在四棱锥S-ABCD中，底面ABCD是正方形，SA⊥底面ABCD，SA＝AB＝2，点M是SD的中点，AN⊥SC，且交SC于点N.

（1）求证：SB∥平面ACM.

（2）求点C到平面AMN的距离.

图5.10

▶　解析

（1）证明：如图5.11所示，连结BD交AC于E，连结ME.

因为ABCD是正方形，所以E是BD的中点.

因为M是SD的中点，所以ME是△DSB的中位线.

故ME∥SB.

又因为ME⊂平面ACM，SB⊄平面ACM，

所以SB∥平面ACM.

（2）由条件有DC⊥SA，DC⊥DA，

所以DC⊥平面SAD，DC⊥AM.

又因为SA＝AD，M是SD的中点，则SD⊥AM，

所以AM⊥平面SDC，SC⊥AM.

图5.11

由已知有SC⊥AN，则SC⊥平面AMN，

于是CN⊥面AMN，则CN为点C到平面AMN的距离.

在Rt△SAC中，SA＝2，

又Rt△SAC～Rt△ANC，于是AC2＝CN·SC，(www.xing528.com)

故点C到平面AMN的距离为

【例3】如图5.12所示，在直四棱柱ABCD-A1B1C1D1中，DB＝BC，DB⊥AC，M是棱BB1上一点.

（1）求证：B1D1∥平面A1BD.

（2）求证：MD⊥AC.

（3）试确定点M的位置，使得平面DMC1⊥平面CC1D1D.

图5.12

▶　解题指南

求解条件探索性问题的主要途径：①先猜后证，即先观察与尝试，猜出条件再证明；②先通过命题成立的必要条件探索出命题成立的条件，再证明充分性.

▶　解析

（1）证明：由直四棱柱ABCD-A1B1C1D1，得BB1∥DD1，且BB1＝DD1，

所以四边形BB1D1D是平行四边形，

则B1D1∥BD.

而BD⊂平面A1BD，B1D1⊄平面A1BD，

所以B1D1∥平面A1BD.

（2）证明：因为BB1⊥平面ABCD，AC⊂平面ABCD，

所以BB1⊥AC.

又因为BD⊥AC，且BD∩BB1＝B，

所以AC⊥平面BB1D.

而MD⊂平面BB1D，则MD⊥AC.

（3）当M为棱BB1的中点时，平面DMC1⊥平面CC1D1D.

证明如下：

如图5.13所示，取DC的中点N，D1C1的中点N1，连接NN1交DC1于点O，连接OM，BN.因为N是DC中点，BD＝BC，所以BN⊥DC.

图5.13

又因为DC是平面ABCD与平面DCC1D1的交线，而平面ABCD⊥平面DCC1D1，所以BN⊥平面DCC1D1.

易证O是NN1的中点，所以BM∥ON，且BM＝ON，

即四边形BMON是平行四边形，则BN∥OM，

所以OM⊥平面CC1D1D.

因为OM⊂平面DMC1，

所以平面DMC1⊥平面CC1D1D.

变式3　1.如图5.14所示，平面ABCD⊥平面BCE，四边形ABCD为矩形，BC＝CE，F为CE的中点.

（1）求证：AE∥平面BDF.

（2）M为CD上任意一点，在线段AE上是否存在点P，使得PM⊥BE？若存在，确定点P的位置，并加以证明；若不存在，请说明理由.

图5.14

▶　解题指南

涉及“点的位置”的探索性问题一般是先根据条件猜测点的位置再给出证明，探索点存在问题，点多为中点或三等分点中的某一个，也可以根据相似知识找出点的位置.

▶　解析

（1）证明：如图5.15所示，连接AC交BD于点O，连接OF.

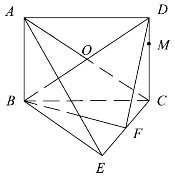
图5.15

因为四边形ABCD是矩形，

所以O为AC的中点.

又因为F为EC的中点，

所以OF∥AE.

因为OF⊂平面BDF，AE⊄平面BDF，

所以AE∥平面BDF.

（2）当点P为AE的中点时，有PM⊥BE.证明如下：

如图5.16所示，取BE的中点H，连接DP，PH，CH.

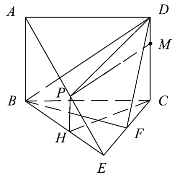
图5.16

因为P为AE的中点，H为BE的中点，所以PH∥AB.

又因为AB∥CD，所以PH∥CD.

故P，H，C，D四点共面.

因为平面ABCD⊥平面BCE，平面ABCD∩平面BCE＝BC，CD⊥BC，CD⊂平面ABCD，所以CD⊥平面BCE.

又因为BE⊂平面BCE，所以CD⊥BE.

因为BC＝CE，且H为BE的中点，

所以CH⊥BE.

又因为CH∩CD＝C，CH，CD⊂平面DPHC，

所以BE⊥平面DPHC.

又因为PM⊂平面DPHC，所以PM⊥BE.

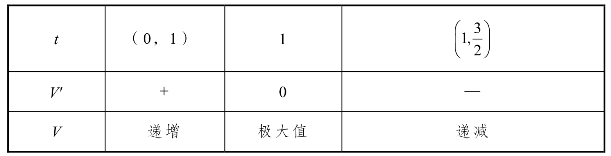
2.如图5.17所示，侧棱垂直于底面的三棱柱ABC-A1B1C1中，AB⊥AC，AA1＋AB＋AC＝3，AB＝AC＝t（t＞0），P是侧棱AA1上的动点.

（1）当AA1＝AB＝AC时，求证：A1C⊥平面ABC1.

（2）试求三棱锥P-BCC1的体积V取得最大值时的t值.

（3）若二面角A-BC1-C的平面角的余弦值为，试求实数t的值.

图5.17

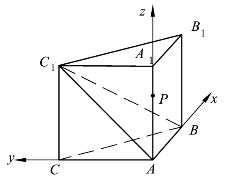
图5.18

巩固提高

1.如图5.19所示，三棱柱ABC-A1B1C1中，D是AB的中点.

（1）求证：AC1∥平面CDB1.

（2）若AA1⊥平面ABC，AC⊥BC，AA1＝1，，求二面角B1-C-B的大小.

图5.19

2.（2019年全国Ⅲ卷理科改编）如图5.20（a）所示，在直角△ABC中，∠ABC＝90°，，D，E分别为AC，BD的中点，连接AE并延长交BC于点F，将△ABD沿BD折起，使平面ABD⊥平面BCD，如图5.20（b）所示.在图5.20（b）中，回答下列问题.

（1）求证：AE⊥CD.

（2）求平面AEF与平面ADC所成锐二面角的余弦值.

图5.20

3.如图5.21所示，在四棱锥P-ABCD中，PA⊥平面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点.证明：

（1）CD⊥AE.

（2）PD⊥平面ABE.

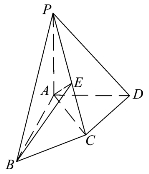
图5.21

4.（2019年黄冈二模）在如图5.22所示的几何体中，平面ADNM⊥平面ABCD，四边形ABCD是菱形，四边形ADNM是矩形，，AB＝2，AM＝1，E是AB的中点.

（1）求证：平面DEM⊥平面ABM.

（2）在线段AM上是否存在点P，使二面角P－EC－D的大小为若存在，求出AP的长；若不存在，请说明理由.

图5.22

5.（2019年湖北省高三适应性考试）如图5.23所示，多面体ABCDB1C1为正三棱柱ABC-A1B1C1沿平面DB1C1切除部分所得，M为CB1的中点，且BC＝BB1＝2.

（1）若D为AA1的中点，求证：AM∥平面DB1C1.

（2）若二面角D-B1C1-B的大小为＝，求直线DB1与平面ACB1所成角的正弦值.

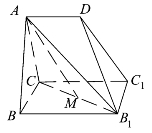
图5.23

6.如图5.24所示的四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是平行四边形，若AD＝2，.AP＝AB＝1.

（1）求证：平面PAC⊥平面PCD.

（2）求棱PD与平面PBC所成角的正弦值.

图5.24