砂性土宏细观特征的颗粒方向统计模型

6.5.4.1　von Mises分布模型

Von Mises分布是一种对圆形数据分析经常采用的对称单峰分布统计模型（Fisher，1993；Jammalamadaka and SenGupta，2001）。Von Mises分布的概率密度函数（Probability Density Function，PDF）计算公式如下：

f（θ）=［2π·I0（κ）］-1exp［κcos（θ-θr）］（0≤θ≤2π，0≤κ≤∞）　（6.19）

式中，θr是颗粒平均方向，κ是集中参数，I0（κ）为修正零阶贝塞尔函数：

一阶修正贝塞尔函数公式与上式相似，且：

θr和r可以通过式（6.16）和式（6.17）算得，则κ可以通过式（6.21）算得。

Von Mises分布的分布函数公式如下：

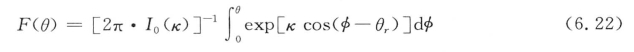
在圆形统计分析中，常常把Von Mises分布看作正态分布，这种分布模型经常被一些学者所采用（Yang，2002）。但对于颗粒方向分布，首先要分析Von Mises分布是否合适。Fisher（1993）认为，在圆形统计分析中，集中参数κ非常重要。当κ≥2时，对模型中一些问题近似处理可以成立，可以采用该模型；当κ＜2时，很难建立与数据分布相一致的模型函数，因此无法采用该模型对数据进行统计分析。所以，κ=2是圆形数据统计分析中的最小可接受值。本书中，平面应变、三轴压缩、直剪试验中的最大κ值分别为0.335、0.532、0.496。所有κ值都小于2，这表明颗粒方向并不服从Von Mises分布。还可以通过拟合度测试来看颗粒方向是否服从Von Mises分布。有两种方法可以对拟合度进行测试：图解法和标准法。在图解法中，首先计算：

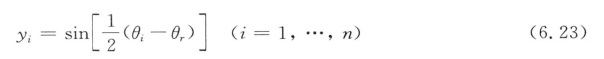
并将它们重新按升序排列，即y1＜…＜yn。按Von Mises分布最佳拟合计算分位数q1，…，qn。最后，绘出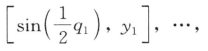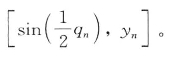如果Von Mises模型与数据拟合度高，那么这一系列点是在通过原点与轴成45°角的直线附近，如图6.34所示。从图中可以看出，颗粒方向并不服从Von Mises分布。

在标准法检验拟合度时，首先通过式（6.22）计算累计频率值fi，再将它们重新按升序排列，即fl＜…＜fn，最后计算统计值：(www.xing528.com)

图6.34　图解法拟合度测试示例（PS-D75-10）

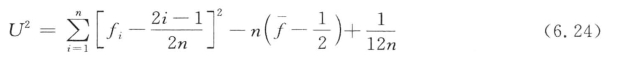
式中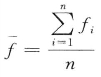，。如果U2比相应κ值对应的临界值大，那么Von Mises分布的假设不成立，说明颗粒方向不服从Von Mises分布。本书中大部分数值模拟试验结果的U2远大于临界值，所以认为颗粒方向不服从Von Mises分布。

6.5.4.2　结构张量与傅里叶级数拟合法

结构可以用来表示集合体内颗粒和孔隙的细观排列方式。在研究颗粒材料时提出了一个重要的概念——结构张量，一些学者采用这一概念研究颗粒材料的细观结构和细观力学（Satake，1978；Oda et al.，1980；Oda et al.，1982；Mehrabadi et al.，1982；Kuo et al.，1998）。有学者做了大量有关结构张量的研究（Rothenburg and Bathurst，1989；Bathurst and Rothenburg，1990；Ouadfel and Rothenburg，2001），提出了一些重要的参数，如接触方向各向异性、接触矢量、接触力各向异性等等，并提出应力—力—结构概念来研究外荷载和这些细观结构参数间的关系（Rothenburg，1980；Ouadfel and Rothenburg，2001）。在这些研究中，Rothenburg和Bathurst（1989）提出了采用傅里叶级数近似分析接触方向、法向接触力和切向接触力分布的方法。研究证明，采用不同级数的傅里叶分析法可以对圆形数据和球形数据进行很好的拟合。这一方法也被一些学者（Ouadfel and Rothenburg，2001）用来分析颗粒方向的分布特征。本书采用傅里叶级数分析法来分析颗粒集合体中颗粒方向的分布。

尽管傅里叶分量的阶数越高计算结果越精确，但是在研究颗粒方向分布时二阶傅里叶分量已经足够满足计算精度要求。对颗粒方向分布，函数P（θ）在θ和θ+π实际上是相等的，所以颗粒方向分布函数P（θ）可以只用傅里叶级数的偶数项表示为：

式中，N为角度分段数，a为表征颗粒方向分布各向异性的参数，θa为各向异性的方向。这种方法不仅可以较好地拟合极状图，还可以求得颗粒方向分布各向异性的程度和角度。a=0时，P（θ）=1/N，表示颗粒方向均匀分布，材料各向同性。需要说明的是，虽然式（6.25）中采用二阶傅里叶分量，但采用更高级数的傅里叶分量可以得到更精确的计算结果。

确定颗粒方向极状图的拟合模型后，下一步需要确定每个极状图的a和θa。以MINPACK算法为基础的Levenberg-Marquardt法是拟牛顿法的一个变化方法，这种方法可以在约束条件下找到误差平方和最小时的参数。本书采用这种算法来确定a和θa的值。

需要注意的是，在傅里叶近似法中，拟合曲线的长轴并不一定与颗粒方向百分比极状图的最大方向相一致。因为拟合曲线的长轴不仅仅由极状图中最大百分比分布的方向决定，还会受到最大百分比颗粒方向周围方向颗粒极状图百分比的影响。也就是说，如果某一方向颗粒方向百分比最大，而这一方向周围的颗粒方向百分比很小，那么这一方向有可能不是拟合曲线长轴的方向。

颗粒方向分布的极状图和相对应的傅里叶级数拟合曲线如图6.35所示。这些图显示了平均方向、平均合向量长度、Rayleigh测试符合程度、各向异性程度、各向异性角度等重要基本参数。采用这一方法，可以对不同荷载条件下不同密实度试样在不同应变条件时颗粒方向的分布特性进行研究。

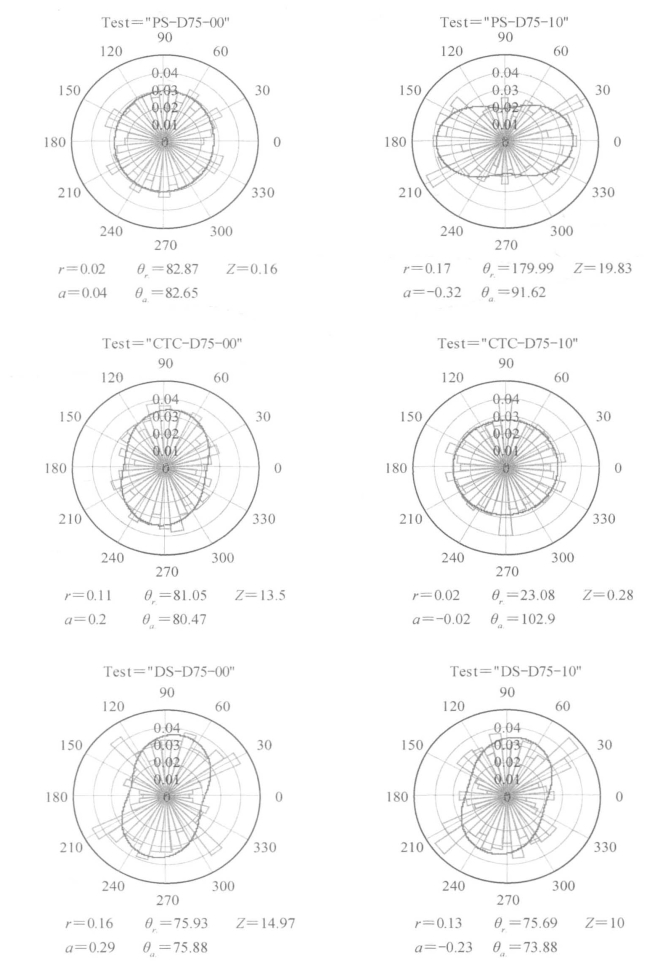
图6.35　试样颗粒方向分布极状图和傅里叶级数拟合曲线示例