非参数方法：协整的表示

1.协整的三角形表示

对于一个存在协整关系的(n×1)向量时间序列yt～I(1)，设其协整矩阵为前述矩阵An×k，则有A′yt的各分量αi′yt～I(0),i＝1,2,…,k 。由于矩阵形式并不唯一，而协整矩阵的秩是不变的，基于此，Phillips（1991）给出了一个协整的三角形表示形式。

设r(A)＝k，则总可以通过初等行变换将An′×k化为如下三角形矩阵：

以使B′yt～I(0)的各分量为平稳过程。

令E(B′yt)＝μ1，则vt＝B′yt－μ1为(k×1)的零均值平稳过程。现将yt分块，形如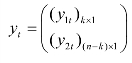：，从而有等式：

式（2-30）可进一步写为：

因为y2t的各分量仍为I(1)序列，根据Wald分解（MA(∞)表述），令E(Δy2t)＝δ2，那么有：

从而得：

联合式（2-31）与（2-32），可表述为矩阵形式：

式（2-33）为协整的三角形表述。显然，该表述形式简洁明了，揭示了协整的内在结构。在进行MC仿真模拟时，可以很方便地表述时间向量的协整关系。利用该表述形式，可进一步研究协整向量的估计及其性质以及假设检验。

2.向量协整的三角形式表述推广：共同趋势形式

将式（2-32）的零均值平稳项u2t＝Δy2t－δ2＝Ψ(L)εt，代入式（2-32）并展开得：

由Beveridge、Stephen与Nelson（1981）观察到Beveridge-Nelson分解，则有：

这里。

令，那么协整的三角形表述形式可化为如下的共同趋势形式：

注意到δ2与ξ2t均为(k×1)向量，故而由式（2-36）可知，协整序列yt是由k个确定趋势的线性组合与k个随机趋势的线性组合之和构成，也即yt的每个分序列都受到共同的确定性趋势和随机趋势的影响，从而表现出亦步亦趋的关系。

3.协整的误差修正模型ECM（Error Corrected Model）表示

当向量yt序列存在协整时，还可以从水平向量自回归和向量移动平均两个角度进行考察。

（1）对于自回归形式，设(n×1)向量yt序列可以表示为p阶水平向量自回归的形式：

记Φ(L)＝In－Φ1L－Φ2L2－…－ΦpLp，则式（2-37）可表示为：

由yt～I(1)，则Φ(L)＝0有一个根在单位圆上，其余在圆外，Φ(L)不可逆。

又由于yt存在协整，A′yt～I(0)，则Φ(1)的各分量可被A′线性表示，即存在一个(n×k)矩阵B使得Φ(1)＝BA′，因而yt可以表为下述向量自回归形式：

其中Φ(1)为(n×n)奇异矩阵。这表明，协整系统可表为受限的VAR形式。

（2）对于移动平均形式，yt～I(1)序列，根据Wald分解（MA(∞)表述），令E(Δyt)＝δ，那么有：(www.xing528.com)

这里εt～i.i.d (0,Ω)，。

又由Beveridge-Nelson分解，式（2-40）可写为：

这里。

式（2-41）两边同时左乘A′，则等式左边A′yt～I(0)，这就要求等式右边也是平稳的，因此有：

从而A′ψ(1)＝0。这也说明ψ(L)不可逆。

因此，yt可以表为下述向量移动平均形式：

对于式（2-42），由于ψ(L)不可逆，因此存在协整关系的向量不能用差分后的变量的有限阶向量自回归表示，即对于存在协整关系的向量不能盲目建立差分VAR模型。

由上述分析可知，存在协整的向量系统，其向量自回归形式和向量移动平均形式都需要一定的限制条件，从而大大限制了这两种形式的应用。

Granger（1987）整合了上述两种形式：

对式（2-39），令

则向量自回归形式可化为：

而Γ0＝Φ1＋Φ2＋…＋Φp－In＝－(Φ(1))，又Φ(1)＝BA′，从而上式可表为：

式（2-44）为误差修正模型ECM形式。由于其具有明显的经济含义，因而得到广泛的应用。

由上述推导可以得到Granger表示定理：

对于(n×1)向量yt序列，其Δyt表述为q阶向量移动平均形式（2-40），满足：εt～i.i.d (0,Ω)，；设yt有k个协整关系，即存在An×k使得A′yt～I(0)，则A满足A′ψ(1)＝0。另外，若yt序列表述成p阶向量自回归形式（2-37），那么存在(n×k)矩阵B使得Φ(1)＝BA′，进一步还存在(n×n)矩阵Γi,i＝1,2,…,p－1，使得式（2-37）等价表述为ECM形式（2-44）。

根据Granger表示定理，任何一个协整关系都可由对应的误差修正模型（ECM）表出，且协整关系对变量的短期变化起调节作用。由于协整关系可以分为确定性协整和随机性协整两种，故而对应了三种ECM设定：

（1）ECM设定1：确定性协整。协整关系中无确定性趋势，ECM中无截距，即

（2）ECM设定2：随机协整。独立的截距出现在ECM中，协整关系中无确定性趋势，即

这一设定意味着各元素具有不同的均值。虽然水平变量具有共同的随机趋势，但截距的各个元素不尽相同，这说明支配各个元素的数据图形的主导因素即确定性趋势不尽相同。因此这是大多数应用研究中应采用的设定形式。

（3）ECM设定3：ECM中无独立的截距，截距只体现在误差修正项中，因而这也是随机协整，即

显然，这种设定的第一项为B(A′yt－1＋A0)，因此，设定3只是设定2的约束(BA0＝μ)表述。

设定2和设定3意味着数据具有确定性趋势。王少平（2002）指出，经验的做法是：若Δyt有不相同的均值，可直接选取设定2，若Δyt有相同的均值，则可选取设定3，或者对单位根使用带截距（趋势）的ADF方程且截距（趋势）项系数显著，选取设定2合适。

协整理论的出现有效防止了人们盲目使用时间序列数据进行回归，而ECM模型的各参数具有明确的含义，从而使该部分成为宏观经济研究的重要组成部分。