二元函数连续性、可偏导性、可微性

例4.3（江苏省2000年竞赛题）　若都存在，则f（x，y）在（x0，y0）　（　）

A.极限存在但不一定连续

B.极限存在且连续

C.沿任意方向的方向导数存在

D.极限不一定存在，也不一定连续

解析　应用二元函数在某点极限存在与可偏导之间无因果关系的结论，A，B皆错.C显见是错的，故选D.

例4.4（江苏省2008年竞赛题）　设

试讨论f（x，y）在（0，0）处的连续性、可偏导性、可微性.

解析　由于

所以，于是f（x，y）在（0，0）处不连续.

由于皆不存在，故f（x，y）在（0，0）处不可偏导.

由于连续性与可偏导性皆是可微性的必要条件，故f（x，y）在（0，0）处不可微.

例4.5（江苏省2002年竞赛题）　设

试讨论f（x，y）在点（0，0）的连续性、可偏导性与可微性.

解析　因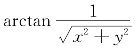有界，所以(www.xing528.com)

故f（x，y）在（0，0）处连续.因为

所以f（x，y）在（0，0）处可偏导.

下面考虑可微性.令

所以ω＝o（ρ），故f（x，y）在（0，0）处可微.

例4.6（江苏省2006年竞赛题）　设

证明f（x，y）在（0，0）处可微，并求.

解析　根据题意可得

所以f在（0，0）处可微，且.

例4.7（江苏省2000年竞赛题）　已知z＝uv，且x＝eucosv，y＝eusinv，求.

解析　由x＝eucosv，y＝eusinv解得

例4.8（江苏省1996年竞赛题）　函数u＝xyz23在点（1，2，－1）处沿曲面x2＋y2＝5的外法向的方向导数为________.

解析已知F＝x2＋y2－5，n＝2（x，y，0），点P（1，2，－1），故曲面在点P的外法向的方向余弦为.又因

例4.9（全国大学生2015年决赛题）　设lj（j＝1，2，…，n）是平面上点P0处的n（n≥2）个方向向量，相邻两个向量之间的夹角为，若函数f（x，y）在点P0有连续的偏导数，证明：.

解析　设