5.4.1 参数估计概述
在许多实际问题中,总体被理解为我们所研究的那个统计指标,它在一定范围内取数值,而且以一定的概率取各种数值,从而形成一个概率分布,但是这个概率分布往往是未知的。例如为了制定绿色食品的有关规定,我们需要研究蔬菜中残留农药的分布状况,对这个分布我们知之甚少,以至于它属于何种类型我们都不清楚。有时我们可以断定分布的类型,例如在农民收入调查中,根据实际经验和理论分析如概率论中的中心极限定理,我们断定收入服从正态分布,但分布中的参数取何值却是未知的。这就导致统计估计问题。统计估计问题专门研究由样本估计总体的未知分布或分布中的未知参数。直接对总体的未知分布进行估计的问题称为非参数估计;当总体分布类型已知,仅需对分布的未知参数进行估计的问题称为参数估计。本节我们研究参数估计问题。本节及以后假定抽样方法为放回简单随机抽样,样本的每个分量都与总体同分布,它们之间相互独立。
5.4.2 参数估计的基本方法
5.4.2.1 估计量与估计值
参数估计就是用样本统计量去估计总体参数。
用来估计总体参数的统计量的名称称为估计量,如样本均值、样本比例、样本方差等都可以是一个估计量。
估计量的具体数值称为估计值。
5.4.2.2 点估计与区间估计
参数估计方法有点估计与区间估计两种方法。
(1) 参数估计的点估计法。
设总体X的分布类型已知,但包含未知参数θ,从总体中抽取一个简单随机样本(X1, X2,…,Xn),欲利用样本提供的信息对总体未知参数θ进行估计。构造一个适当的统计量 =T(X1,X2,…,Xn)作为θ的估计,称
=T(X1,X2,…,Xn)作为θ的估计,称 为未知参数θ的点估计量。当有了一个具体的样本观察值(x1,x2,…,xn) 后,将其代入估计量中就得到估计量的一个具体观察值T(x1,x2,…,xn),称为参数θ的一个点估计值。今后点估计量和点估计值这两个名词将不强调它们的区别,通称为点估计,根据上下文不难知道此处的点估计究竟是点估计量还是点估计值。
为未知参数θ的点估计量。当有了一个具体的样本观察值(x1,x2,…,xn) 后,将其代入估计量中就得到估计量的一个具体观察值T(x1,x2,…,xn),称为参数θ的一个点估计值。今后点估计量和点估计值这两个名词将不强调它们的区别,通称为点估计,根据上下文不难知道此处的点估计究竟是点估计量还是点估计值。
通俗地说,用样本估计量的值直接作为总体参数的估计值称为点估计。
(2) 参数估计的区间估计法。
在参数估计中,虽然点估计可以给出未知参数的一个估计,但不能给出估计的精度。为此人们希望利用样本给出一个范围,要求它以足够大的概率包含待估参数真值。这就是导致区间估计问题。
定义5.3 设θ是未知参数,(X1,X2,…,Xn)是来自总体的样本,构造两个统计量 =T1(X1,X2,…,Xn)
=T1(X1,X2,…,Xn) =T2(X1,X2,…,Xn),对于给定的α(0<α<1),若
=T2(X1,X2,…,Xn),对于给定的α(0<α<1),若 满足
满足
 ,则称随机区间
,则称随机区间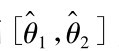 是参数θ的置信水平为1-α的置信区间,1-α称为
是参数θ的置信水平为1-α的置信区间,1-α称为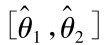 的置信系数
的置信系数 称为置信限。
称为置信限。
这里有几点需要说明:
第一,区间 的端点
的端点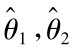 及长度
及长度 都是样本的函数,从而都是随机变量,因此
都是样本的函数,从而都是随机变量,因此 是一个随机区间。
是一个随机区间。
第二 表明随机区间
表明随机区间 以1-α的概率包含未知参数真值,区间长度
以1-α的概率包含未知参数真值,区间长度 描述估计的精度,置信水平1-α描述了估计的可靠度。
描述估计的精度,置信水平1-α描述了估计的可靠度。
第三,因为未知参数θ是非随机变量,所以不能说θ落入区间 的概率是1-α,而应是随机区间
的概率是1-α,而应是随机区间 包含θ的概率是1-α。
包含θ的概率是1-α。
通俗地说,在点估计的基础上,给出总体参数的一个范围称为区间估计。
5.4.3 总体均值的区间估计
区间估计必须同时具备三个要素,即具备估计值、抽样极限误差和概率保证程度三个基本要素。抽样误差范围决定抽样估计的准确性,概率保证程度决定抽样估计的可靠性,二者密切联系,但同时又是一对矛盾,所以,对估计的精确度和可靠性的要求应慎重考虑。
在实际抽样调查中,区间估计根据给定的条件不同,有两种估计方法:(1) 给定极限误差,要求对总体指标做出区间估计;(2) 给定概率保证程度,要求对总体指标做出区间估计。
[例5.3]某企业对某批电子元件进行检验,随机抽取100只,测得平均耐用时间为1000小时,标准差为50小时,合格率为94%,求:
(1)以耐用时间的允许误差范围Δx=10小时,估计该批产品平均耐用时间的区间及其概率保证程度。
(2) 以合格率估计的误差范围不超过2.45%,估计该批产品合格率的区间及其概率保证程度。
(3) 试以95%的概率保证程度,对该批产品的合格率做出区间估计。
解:(1) 求样本指标:
 =1000(小时) σ=50(小时)
=1000(小时) σ=50(小时)
μx= =5(小时)
=5(小时)
根据给定的Δx =10小时,计算总体平均数的上、下限:
下限 -Δx=1000-10=990(小时)
-Δx=1000-10=990(小时)
上限 +Δx=1000+10=1010(小时)
+Δx=1000+10=1010(小时)
根据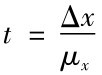 =2,查概率表得:
=2,查概率表得:
F(t) =95.45%
由以上计算结果,估计该批产品的平均耐用时间为990 ~1010小时,有95.45%的概率保证程度。
(2) 求样本指标:
p=94% σ2p=p(1-p) =0.0564
μp= =2.38%
=2.38%
根据给定的Δp =2.45%,求总体合格率的上、下限:
下限p-Δp =94% -2.45% =91.55%
上限p+Δp =94% +2.45% =96.45%
根据t=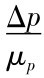 =1.03,查概率表得:
=1.03,查概率表得:
F(t) =69.70%
由以上计算结果,估计该批产品的合格率为91.55% ~96.45%,有69.70%的概率保证程度。
(3) 求样本指标:
σ2p=p(1-p) =0.0564
μp= =2.37%(https://www.xing528.com)
=2.37%(https://www.xing528.com)
ΔP=t·μp=0.046
下限p-Δp =94% -4.6% =89.4%
上限p+Δp =94% +4.6% =98.6%
所以,以95%的概率保证程度估计该批产品的合格率在89.4% ~98.6%。
情况一:当σ2已知时,求μ的置信区间。
[例5.4]某种零件的长度服从正态分布,从该批产品中随机抽取9件,测得它们的平均长度为21.4毫米,已知总体标准差为σ=0.15毫米,试建立该种零件平均长度的置信区间,假定给定置信水平为0.95。
解:已知 =21.4,因为U=
=21.4,因为U= ~N(0,1),所以对于给定的置信水平0.95,有
~N(0,1),所以对于给定的置信水平0.95,有 。当α=0.05时,分位点Uα/2=1.96,有:
。当α=0.05时,分位点Uα/2=1.96,有:
即总体均值的置信区间为[21.302,21.498]。有95% 的概率保证该种零件的平均长度为21.302 ~21.498毫米。
情况二:当σ2未知时,求μ的置信区间。
不知道总体方差时,一个很自然的想法是用样本方差来代替,这时,需要考虑的问题是,用样本方差代替总体方差后,统计量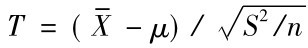 服从的是什么分布,以下定理给出了统计量T的分布形式。
服从的是什么分布,以下定理给出了统计量T的分布形式。
定理 设x1,x2,…,xn是来自总体N(μ,σ2)的一个样本,则:
t分布具有如下特性:
第一,t分布与标准正态分布相似,是以x=0为对称轴的钟形对称分布,但是t分布的方差大于1,比标准正态分布的方差大,所以从分布曲线看,t分布的曲线较标准正态分布平缓。
第二,t分布的密度函数为: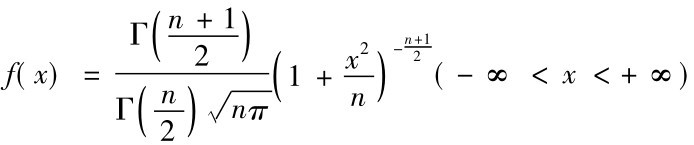
t分布的密度函数中只有一个参数,称为自由度。如果随机变量X具有以上形式的分布密度,则称X服从自由度为n的t分布,记为X~t(n)。随着自由度的增大,t分布的变异程度逐渐减小,其方差逐渐接近1,当n→∞时,t分布成为正态分布。
第三,随机变量X落在某一区域内的概率,等于t分布曲线下相应区域的面积,对于不同的n,同样的区域下的概率不同。如n=10,X落入[-1.372,+1.372]区间的概率为0.9;而当n =20时,概率为0.9所对应的区间为[-1.325,+1.325];当n =30时,概率为0.9所对应的区间为[-1.31,+1.31]。
关于t分布的特性就讨论到此,现在回到如何应用t分布求解置信区间的问题,既然定理已经证明了统计量 服从n个自由度的t分布,则对于给定的显著性水平α,不难找出tα/2(n-1),使得
服从n个自由度的t分布,则对于给定的显著性水平α,不难找出tα/2(n-1),使得 。于是得到以1-α置信水平保证的置信区间为:
。于是得到以1-α置信水平保证的置信区间为:
[例5.5]某研究机构进行了一项调查来估计吸烟者一月花在抽烟上的平均支出,假定吸烟者买烟的月支出近似服从正态分布。该机构随机抽取了容量为26的样本进行调查,得到样本平均数为80元,样本标准差为20元,试以95%的把握估计全部吸烟者月均抽烟支出的置信区间。
解:已知 =80,S=20,n=26,1-α=0.95。由于不知道总体方差,所以用样本方差代替。因为
=80,S=20,n=26,1-α=0.95。由于不知道总体方差,所以用样本方差代替。因为 。
。
根据α=0.05,查阅t分布表得:t0.05/2(25) =2.06
所以有 ,代值得总体的置信区间为[71.92,88.08],即有95%的把握认为吸烟者月均抽烟支出在71.92 ~88.08元。
,代值得总体的置信区间为[71.92,88.08],即有95%的把握认为吸烟者月均抽烟支出在71.92 ~88.08元。
情况三:单个非正态总体或总体分布未知,求U的置信区间。
当总体为非正态分布,或不知总体的分布形式时,只要知道总体方差,那么当n很大时,统计量 就近似服从标准正态分布,经验上,n >30就可以认为是大样本。
就近似服从标准正态分布,经验上,n >30就可以认为是大样本。
[例5.6]设某金融机构共有8042张应收账款单,根据过去记录,所有应收账款的标准差为3033.4元。现随机抽查了250张应收款单,得平均应收款为3319元,求98%置信水平的平均应收款。
解:已知 =3319元,n=250>30,1-α=0.98,σ=3033.4。
=3319元,n=250>30,1-α=0.98,σ=3033.4。
因为 近似服从标准正态分布,Uα/2=2.33,则总体均值的置信区间为:
近似服从标准正态分布,Uα/2=2.33,则总体均值的置信区间为:
根据调查结果,我们有98%的把握认为全部账单的平均金额至少为2871.99元,至多为3766元。
以上例题虽然不知总体分布形式,但总体的方差是已知的,而在实际中往往并不知道总体的方差,在实际应用中,只要是大样本,则仍然可以用样本方差代替统计量中的总体方差,并以标准正态分布近似作为统计量的抽样分布。
5.4.4 总体方差的区间估计
数理统计证明,对于容量为n的正态总体样本方差S2,若总体方差为σ2,则 服从自由度为n-1的χ2分布。对给定的置信系数1-α,查χ2分布表可得上
服从自由度为n-1的χ2分布。对给定的置信系数1-α,查χ2分布表可得上 分位点
分位点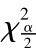 (n- 1)和下1-
(n- 1)和下1- 分位点
分位点 (n-1),使得:
(n-1),使得:
有 ,取
,取 ,则
,则 即σ2的置信水平为1-α的置信区间,也即
即σ2的置信水平为1-α的置信区间,也即 。
。
[例5.7]食品厂从生产的罐头中随机抽取15个称量其重量,得样本方差S2=1.652,设罐头重量服从正态分布,试求其方差的置信水平为90%的置信区间。
解:1-α=0.9,α=0.1,查χ2分布表得:
故总体方差的置信水平为90%的置信区间为[1.61,5.8]。
5.4.5 样本大小的确定
5.4.5.1 影响样本大小的因素
在抽取样本时样本容量应多大是一个很实际的问题。样本容量取得比较大,收集的信息就比较多,从而估计精度比较高,但进行观测所投入的费用、人力及时间就比较多;样本容量取得比较小,则投入的费用、人力及时间就比较少,但收集的信息也比较少,从而估计精度比较低。这说明精度和费用对样本量的影响是矛盾的,不存在既使精度最高又使费用最省的样本量。一个常用的准则是在使精度得到保证的前提下寻求使费用最省的样本量。由于费用通常是样本量的正向线性函数,故使费用最省的样本量也就是使精度得到保证的最小样本量。
5.4.5.2 估计总体均值时样本大小的确定
在简单随机重复抽样下,设样本(X1,X2,…,Xn)来自正态总体N(μ,σ2),总体均值μ的点估计为样本均值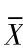 。如果要求以
。如果要求以 估计μ时的绝对误差为d,可靠度为1-α,即要求
估计μ时的绝对误差为d,可靠度为1-α,即要求 。由
。由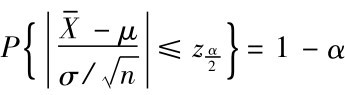 知
知 ,故只需取绝对误差
,故只需取绝对误差 ,从而解得
,从而解得 。
。
[例5.8]在某企业中采用简单随机抽样调查职工月平均奖金额,设职工月奖金额服从标准差为10元的正态分布,要求估计的绝对误差为3元,可靠度为95%,应抽取多少名职工?
解:已知σ=10,d=3,1-α=0.95 =1.96,则:
=1.96,则:
即需抽取43名职工作为样本进行调查。
5.4.5.3 估计总体比例时样本大小的确定
在简单随机重复抽样条件下估计总体比例时,可以定义绝对误差 ,从而得到样本容量:
,从而得到样本容量:
[例5.9]根据以往的生产统计,某种产品的合格率为90%,现要求绝对误差为5%,在置信水平为95%的置信区间时,应抽取多少个产品作为样本?
解:π=90%,d=5%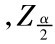 =1.96,则:
=1.96,则:
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




