用矩阵相似变形法解决特征值问题

利用矩阵相似变形来求解特征值的方法，基于以下两个矩阵的性质：

①相似矩阵A、B的特征值相同。所谓相似，是指二者满足A=C^TBC，其中，C为正交矩阵（C^-1=C^T）。

②对角矩阵的特征值等于其对角项上的元素。

对于动力学问题，对刚性矩阵和质量矩阵进行相似变换，达到

则对角矩阵Λ的对角项就是系统的特征值，Φ为系统的特征向量矩阵。

因此，构建以下迭代关系

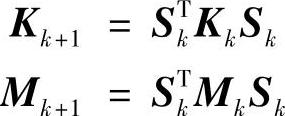
选择变换矩阵S，经过n次迭代使得刚性矩阵和质量矩阵趋于对角化，并满足关系式（5.73），则有

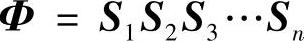
1.Jacobi变换法

对于M=I的标准特征值问题Kφ=λφ，传统的相似变形方法是利用Jacobi变换的方法。对于大规模系统来说，尽管该方法已被更有效的方法所取代，但由于该方法是理解和掌握其他方法的基础，所以本节结合一个具体例子，对该方法的原理进行说明。

对于对称矩阵K，为了使非对角元素K_ij变为0，定义下列Jacobi变换矩阵（也称Jacobi旋转矩阵）

其中，θ由以下关系式给出

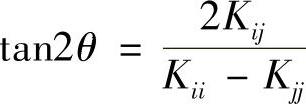
如果K_ii=K_jj，则θ=π/4。于是，相似变形后的矩阵S^T_kKS_k在第i行，第j列上的元素K_ij变为0。

作为举例，考察下列刚性矩阵的特征值

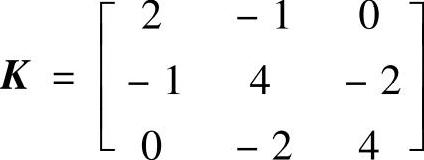
把上述矩阵作为K₁，为了使位置i=1，j=2上的元素-1变为0，构建下列Jacobi矩阵

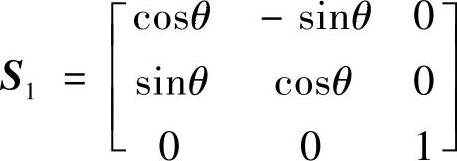
这里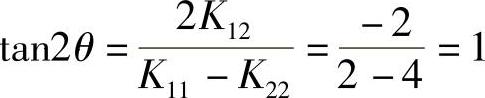，，得cosθ=0.9239，sinθ=0.3827。变形后的刚性矩阵为

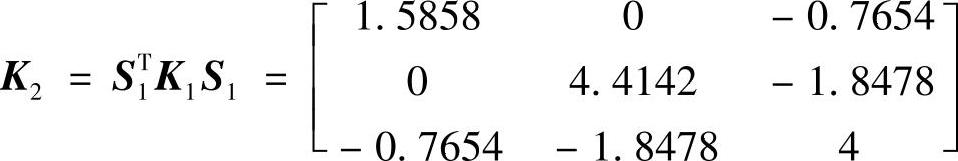
下一步，为了使位置i=1，j=3上的元素-0.7654变为0，构建下列Jacobi矩阵

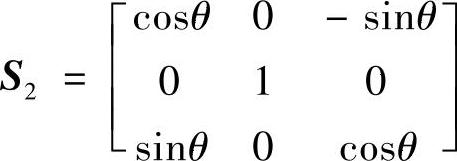
其中，cosθ=0.9604，sinθ=0.2788。

得到

注意：在前面的变换中已经变为0的元素，在以后的变换中可能又不为0。

再下一步，为了使位置i=2，j=3上的元素-1.7745变为0，构建下列Jacobi矩阵

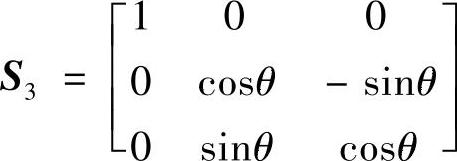
其中，cosθ=0.7260，sinθ=0.6877。

得到

以上就是经过一轮变换运算后的结果。尽管矩阵K₄的非对角项变小了，但是远没有达到对角矩阵的要求。因此，还需要重新扫描一遍以上变换过程。

省略掉具体步骤，经过第二轮迭代变换后，得到以下结果

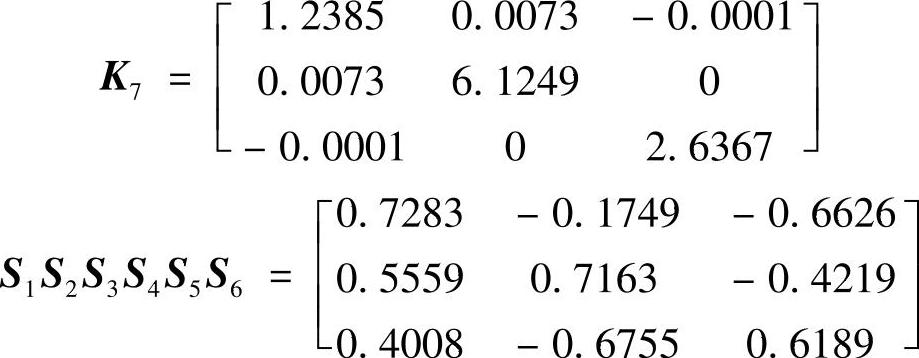
再经过一轮迭代变换，得到满足要求的以下结果

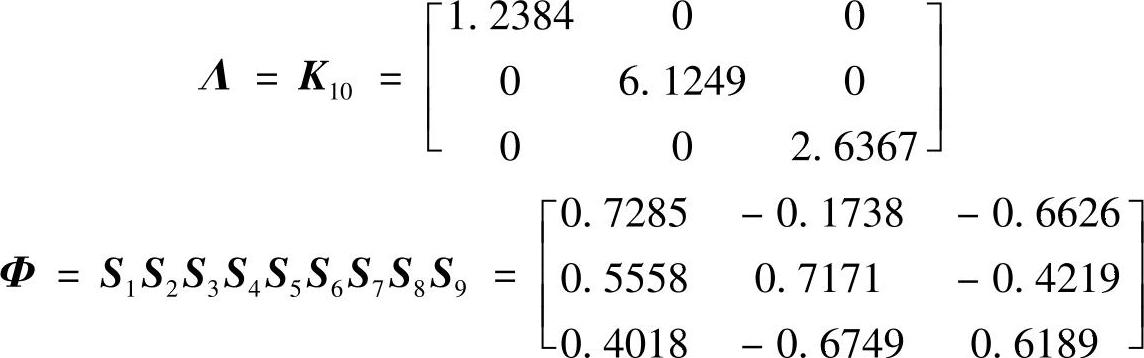
可见，该系统的特征值与特征向量为

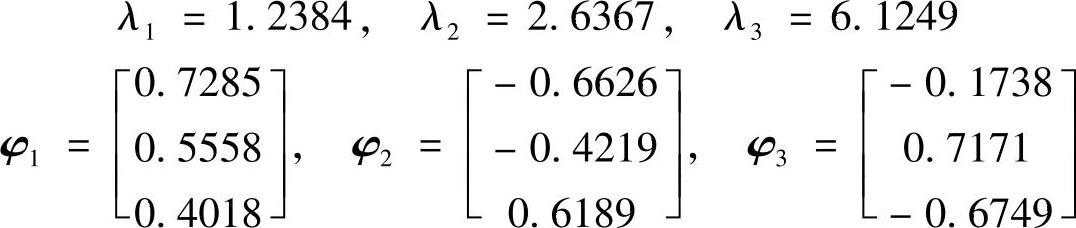
以上是针对标准特征值问题的Jacobi方法。对于一般化特征值问题，可以先转化为标准问题，再应用上述方法。此外，现在已开发出了直接针对一般化特征值问题的扩展Jacobi方法，这里就不做介绍。

Jacobi方法的特点是：可以同时得到全部的特征值以及特征向量，结构简单，稳定性好。对于小规模系统，该方法仍然不失为一种有效的方法。

2.Householder-QR变换法

上面介绍的Jacobi法，是利用矩阵相似变形的迭代运算，把刚性矩阵变换为对角阵。对于大规模有限元模型来说，这个方法的计算效率不高。现在，在处理矩阵特征值问题时，通常先把矩阵转换为一个3重对角矩阵，然后再变换为对角阵。最初出现的3重对角化方法是Givens法，它是对Jacobi法的变形；后来开发出来的Householder法的运算次数减半，因而得到了普及。对于大型稀疏矩阵，更有效的方法是Lanczos法。这里，我们对Householder法做以简要介绍；至于Lanczos法，由于属于混合法，单独作为一节在5.4.4节中介绍。

首先，对3重对角矩阵的定义做一说明。所谓3重对角矩阵，是指对角线及其相邻的上下位置的元素不为0，而其他位置的元素为0的矩阵。例如以下矩阵就是3重对角矩阵

3重对角矩阵是Hessenberg矩阵的特殊形式。如果上面矩阵中的右上方的3个0元素不为0，则为一般形式的上方Hessenberg矩阵；相反，如果上面矩阵中的左下方的3个0元素不为0，则为一般形式的下方Hessenberg矩阵。

Householder变换是把一个向量或矩阵以一个平面或超平面为镜面进行反射的变换方法。如图5.14所示，在XY坐标系上有一单位向量w，把它以向量u所在的垂直于纸面的平面为镜面进行反射，得到新的单位向量w′。现在来考察w与w′的关系。设超平面的法线方向为v，则在UV坐标系中，单位向量w与w′可以分别表示为

w=au₀+bv₀ （5.75a）

w′=au₀-bv₀ （5.75b）

这里，a、b为常数，且有a²+b²=1。u₀、v₀分别为u、v方向上的单位向量。由于u正交于v，给式（5.75a）两边同乘以v₀，并利用v₀v₀=1，u₀v₀=0可得

b=wv₀

另外，对式（5.75b）做以下变形，并将b=wv₀代入得

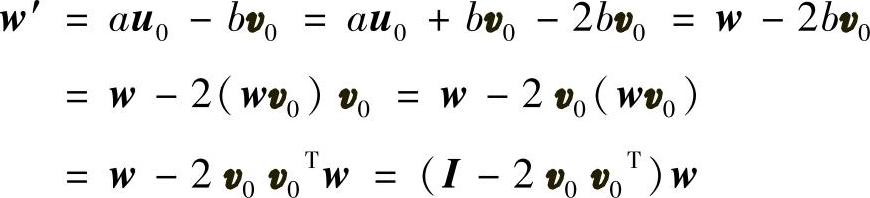
可见，向量w的镜面反射w′可以由下列矩阵变换得到

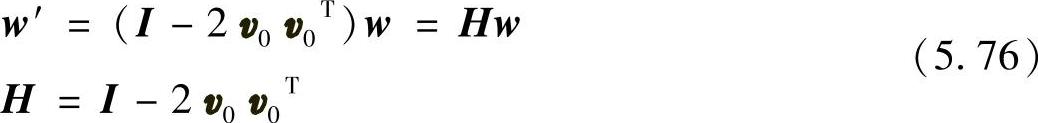
其中，H为Householder反射矩阵，I为单位矩阵。式（5.76）所代表的变换称为向量的Householder变换。显然，单位向量v₀与（w-w′）同向，因而有以下关系

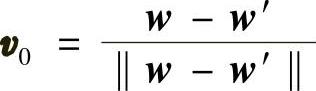(www.xing528.com)

Householder变换矩阵既是对称矩阵，又是正交矩阵，即H^T=H，H^TH=I。由于Householder变换是镜面反射变换，因此变换前后向量的长度（模）保持不变。根据此性质，如果变换后的向量中有一个元素的大小等于变换前的向量的模，则其余元素必为0。所以，应用Householder变换，可以把一个向量转换为一个元素不为零、其余元素均为零的向量。下面通过一个例子来说明。

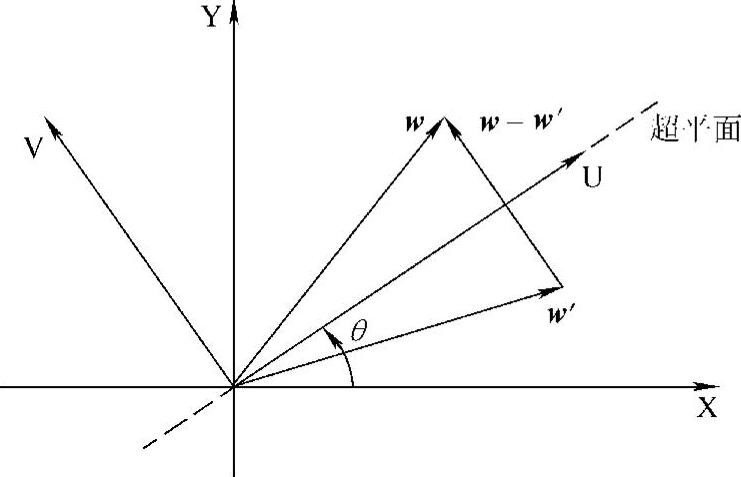
图5.14 镜面反射的原理

有一个向量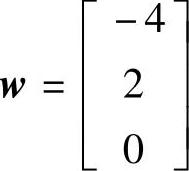，现在来决定一个Householder变换，以使该向量变为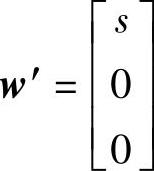的形式。这里，s代表不为0的元素。由于Householder变换后向量的模不变，因此有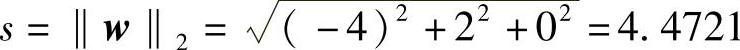。构建以下向量

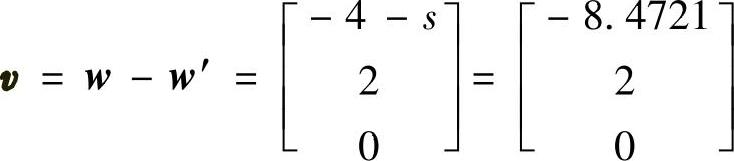
则可以得到Householder矩阵

作为验证，。

利用以上方法，我们可以把一个一般矩阵K通过以下变换，转化为一个3重对角阵

K′=H^TKH=HKH （5.77）

为了说明该方法，假定K为n阶对称矩阵，把矩阵表示如下

K₁=K=[k₁k₂…k_n]

其中，k_i为矩阵的第i列，k_i=[K_1iK_2i…K_ni]^T。对每列进行适当的Householder变换，就可以把矩阵变为3重对角阵。

例如为了将第1列k₁的次对角项下方的所有元素变为0，变换矩阵可以取为以下的形式

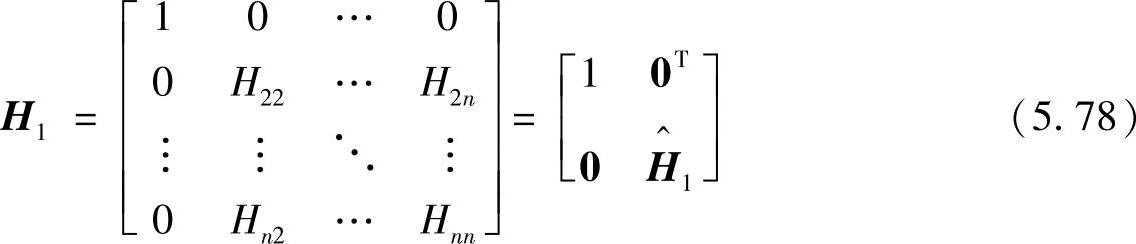
并且使

这里，0代表n-1阶零向量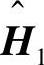，代表n-1阶变换矩阵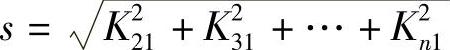，。根据矩阵乘法规则可以得到

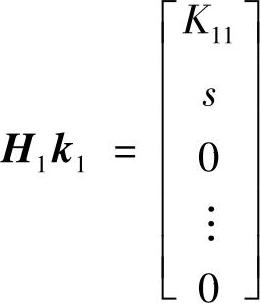
即向量k₁被变换成了第3个元素以下（次对角项下方）均为0的新向量。

满足式（5.79）的Householder变换矩阵为

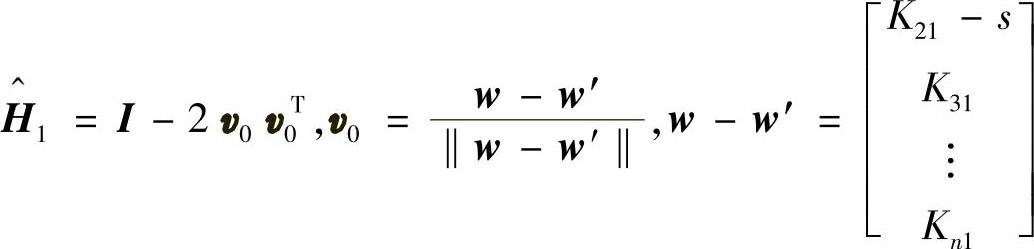
于是可得变换后的矩阵为（利用K对称的性质）

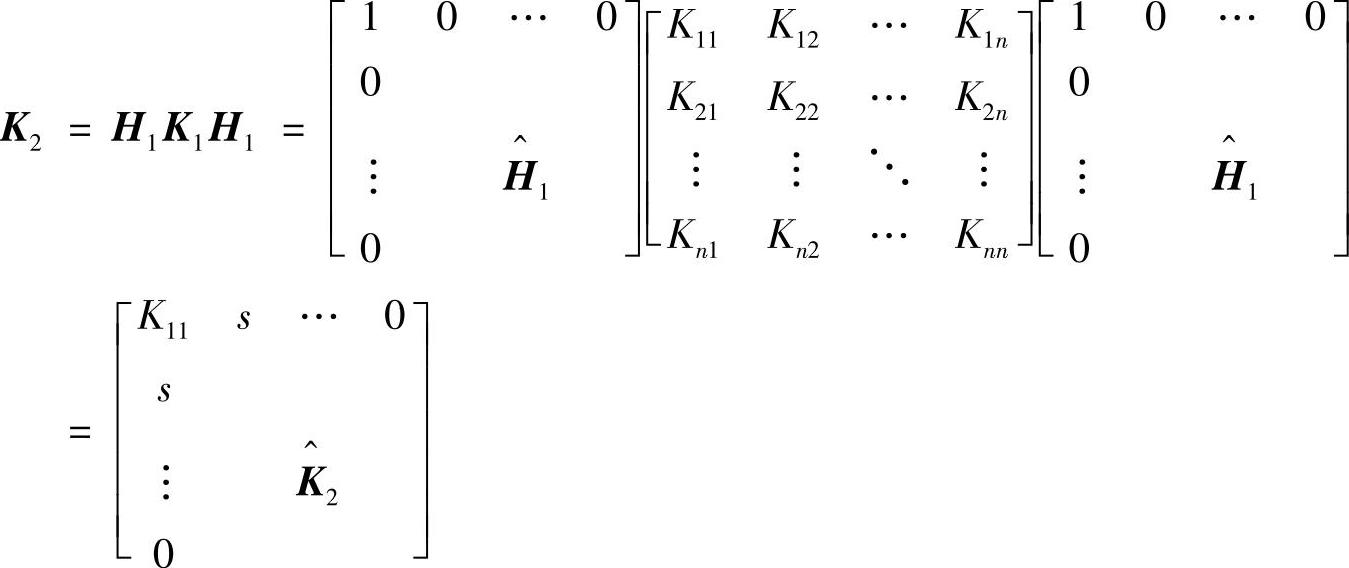
对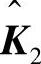进行同样的处理，并以此类推，总共经过n-2次变换，可以把K变为3重对角阵。

作为举例，对下列矩阵进行Householder变换

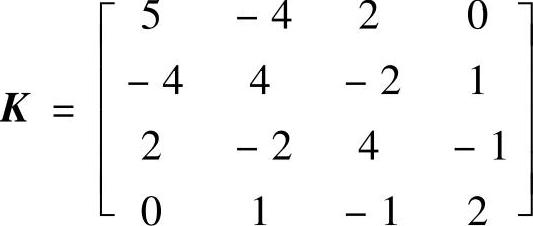
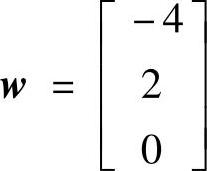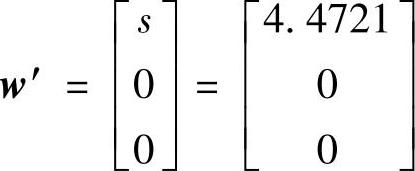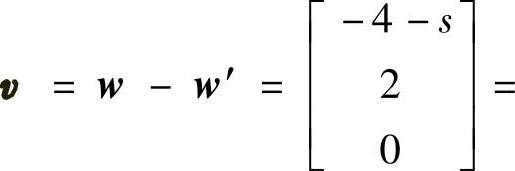
首先构建向量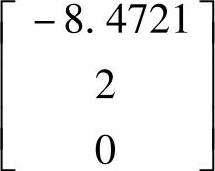，，，可得

然后构建向量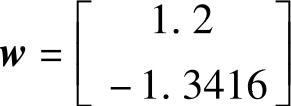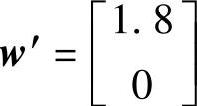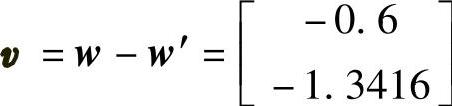，，，可得

可见，经过二次变换，就把原有矩阵变为3重对角阵。

矩阵3连乘H^TKH的计算量为2n³，对于大规模系统来说，计算负荷会很大。因此，在实际的算法中，利用Householder矩阵的特点对3连乘予以回避。具体方法请参阅有关书籍。

利用Householder变换把矩阵K转化为3重对角阵后，还需要进一步利用相似变形把它转化为对角阵才能得到特征值的解。QR变换就是常用的方法。

以下是关于QR分解和QR变换的定义。

一个实矩阵A，不论是否对称，可以唯一地分解为一个正交矩阵Q与一个上三角矩阵R的乘积，即A=QR。上述分解称为矩阵的QR分解。

对于线性动力学系统来说，一般刚性矩阵K为对称矩阵。应用QR分解可得

K=QR

由于Q是正交矩阵，Q^TQ=I。现在我们来考察矩阵RQ

RQ=IRQ=Q^TQRQ=Q^TKQ

可见，矩阵RQ原来是矩阵K的相似变换，称为QR变换。

据此，我们可以得到基于QR变换的迭代算法的步骤为

① 对K进行QR分解，K=QR。

② 令K₁=RQ=Q^TKQ。

③ 对K₁进行QR分解，K₁=Q₁R₁。

④ 令K₂=R₁Q₁=Q^T₁K₁Q₁。

⑤ 对K₂进行QR分解，K₂=Q₂R₂。

⑥ 令K₃=R₂Q₂=Q₂^TK₂Q₂。

⑦ 依次类推。经过r次迭代运算，最终可以把对称矩阵K变为对角阵Λ，其对角项就是系统的特征值。与特征值对应的特征向量矩阵为Φ=Q₁Q₂…Q_r（对于K为非对称矩阵的情况，上述变换最终把K变为上三角矩阵）。

上述方法的关键是进行QR分解。利用Gram-Schmidt正交化方法对矩阵K的每个列向量进行处理，即可得到K的QR分解。也可以利用前面介绍的Jacobi变换方法。对一个n阶一般矩阵进行QR分解需要的计算量为O（n³），而对一个3重对角阵进行QR分解只需O（n）的运算量。因此，在进行QR分解之前，先用House-holder变换把矩阵转化为3重对角阵，从而可以提高计算效率。这正是把House-holder变换与QR分解结合起来构成Householder-QR算法的原因。

下面，我们利用Matlab的函数qr（ ）来进行QR迭代，对象为前面的例子中利用Householder变换得到的3重对角阵

利用表5.4所示的Matlab程序，当迭代16次时，可以得到满意的结果，如Λ与Φ所示。

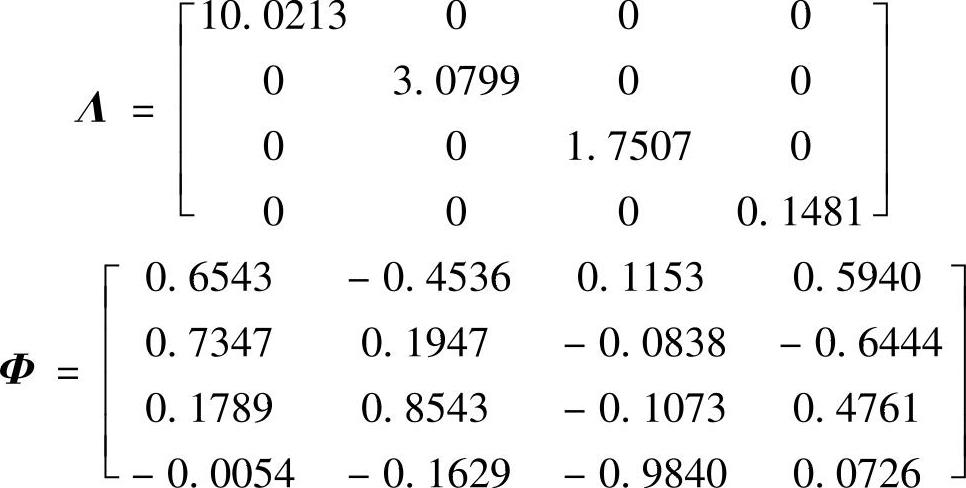
最后需要指出的是，Householder-QR变换法只适用于标准特征值问题。对于一般化特征值问题，首先应转化为标准特征值形式，才能应用该方法。

表5.4 进行QR迭代变换的Matlab程序