多载波微放电中二次电子横向扩散的概率分析

上述的多载波微放电统计理论均是针对理想平行平板结构，不适用于电场非均匀分布的情况。而绝大多数的大功率微波部件均采用矩形波导、同轴波导和圆波导等具有非均匀场分布模式的结构实现。因此，研究非均匀电场中二次电子的演化过程，进而得到多个包络周期多载波微放电阈值，对大功率微波部件设计具有重要的指导意义。

由于多载波微放电统计理论计算过于耗时，并且只适用于平行平板结构，为了实现复杂结构微波部件多个包络周期微放电“最坏状态”分析，Anza等［6］提出了准稳态方法（Quasi－Stationary，QS），即将多载波信号看作幅度按多载波瞬时幅度变化、频率为中心频点的单载波信号，采用非稳态单载波微放电统计理论进行电子增长和吸收过程的计算，并采用平行平板等效来实现方波导类结构微波部件的多载波微放电的等效分析。由于将多载波处理为中心频率的单载波，该方法只适用于窄带的情况，对于实际的多载波宽带微波部件微放电分析误差过大。

进行非均匀场条件下二次电子累积计算的关键是得到微放电过程中二次电子在大功率腔体中横向扩散的物理描述。在均匀场条件下，二次电子的横向扩散在概率上是均匀、各向同性的，因此在二次电子累积计算中不必考虑横向扩散的因素；但在非均匀场中，二次电子的横向扩散不再各向同性，因此必须在理论计算中计入横向扩散的影响。

本节采用概率方法对非均匀场中的多载波微放电进行理论分析，通过引入随机漫步（Random Walk）和Branching Levy漫步（Branching Levy Walk）模型，对微放电过程中二次电子横向扩散所需遵循的概率模型进行了严格的推导，并采用所得的概率密度函数，给出了主模为TE10模式的矩形波导中多载波微放电二次电子积累过程的理论计算［7］。

上述所有的微放电统计理论均基于二次电子发射模型中二次电子出射速率和角度的概率密度分布［8］。二次电子发射的方位角φ和极角θ的定义如图3－6所示，碰撞于固体表面的微观粒子，其逸出表面的方向与原入射方向无关，并按与表面法线方向所成角度的余弦进行分布［8］。微观粒子离开固体表面时，处于立体角dΩ中的概率为：

图3－6　二次电子发射的方位角φ和极角θ示意图

其中，立体角dΩ＝sinθdθdφ，代入式（3－26）可得：

为了求得方位角φ的概率密度函数f（φ），对式（3－27）在θ∈［0，π／2］范围内进行积分：

式（3－28）的积分部分等于1／2，因此可以得到二次电子发射的方位角φ的概率密度分布为均匀分布：

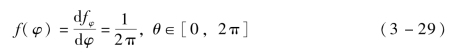
同样，为了求得极角θ的概率密度函数f（θ），对式（3－27）在φ∈［0，2π］范围内进行积分：

进而得到二次电子发射的方位角θ的概率密度分布为：

对二次电子角度余弦分布的一种常见错误解读是认为极角θem的概率密度分布就是余弦分布f（θ）＝cosθ。这种误解通常发生在二维问题建模时，误解的原因是没有认识到三维立体角与二维平面角度之间还存在sinθ的关系。本节将基于上述模型和概率密度分布，同时引入随机漫步理论，利用概率方法，严格推导二次电子横向扩散的概率密度分布。

以矩形波导的TE10模式为例进行非均匀场条件下的多载波微放电分析。图3－7为非均匀场中多载波微放电的理论分析模型。由图可见，在x－y截面，电场沿着x方向并非均匀分布，因此Anza给出的均匀场条件下的理论分析方法并不适用［5］。

图3－7　非均匀场中多载波微放电的理论分析模型［7］

（a）在x－y－z坐标系中的矩形波导；（b）TE10模式的横向电场分布

为了计算上述非均匀场中的多载波微放电，可以将其横向截面均匀分割成若干区域，如图3－7（b）所示。当这些区域的数量足够多时，每个区域内的电场可以视为均匀场，从而每个区域内积累的二次电子可以采用Anza的方法进行计算。但是，在将每个区域的二次电子数量累加、计算腔体内部总的二次电子累积时，我们还需要知道不同区域之间的二次电子的横向扩散，从而在迭代计算中将总的二次电子数量合理地分配到各个区域。

首先将图3－7中的均匀场区域等效为平行板波导，并考虑二次电子在平行板间的碰撞和横向扩散，如图3－8中的俯视图（左）和侧视图（右）所示。其中，图3－8（a）中SEY恒为1，即电子的每次碰撞仅导致1个二次电子的逸出；图3－8（b）中SEY恒为1.28，即单个电子经9次碰撞后，累积二次电子的概率数量为11。通过将图3－8中二次电子的运动与布朗运动进行类比，可以引入随机漫步和Branching Levy漫步模型对二次电子的随机运动行为进行概率分析。

首先，考虑SEY＝1的情况，此时二次电子的运动与布朗运动（Brownian motion）类似，不同之处是：布朗运动中微小颗粒（如灰尘）的随机漫步来源于与大量周边粒子（如空气分子）的随机碰撞；而本节中，二次电子的随机漫步来源于与平行导体平面的大量随机碰撞。如前所述，在每次碰撞后，二次电子的逸出角度θ满足概率密度函数f（θ）＝sin2θ。同时，其逸出方位角φ满足概率密度函数f（φ）＝1／2π。在图3－8（a）中，平行板间二次电子的运动由一系列随机路径组成，每条路径都对应一个由f（θ）和f（φ）决定的反射角。理论上，二次电子在平行板之间的渡越时间由逸出速度和加速电场共同决定的，其中逸出速度满足麦克斯韦概率分布。但在本节中，由于二次电子在平行金属表面间的随机碰撞与多载波加速电场完全不同步，对于大量的随机碰撞而言，粒子被电场加速和减速的宏观概率相等，因此，加速电场对横向扩散的影响可以忽略，可认为上述随机漫步路径与加速电场无关［9］。

假设二次电子在指定的横向方向（如x方向）扩散的概率密度函数为f（lx）。其中，lx是每次碰撞后二次电子横向扩散在x方向的分量，如图3－8（a）所示。如果第i次碰撞引起的横向扩散在x方向的分量为lx，i，经n次碰撞后沿x方向总的横向扩散位移为：

图3－8　均匀场中二次电子横向扩散［7］

（a）随机漫步；（b）Branching Levy漫步(www.xing528.com)

根据概率论中心极限定理，如果f（lx）的两类距量

均为有限值时，二次电子横向扩散的特征与一维布朗运动一致，Ln的分布将符合高斯形式，其中μ为Ln的均值，σ为标准高斯分布G（0，σ2）的标准差；如果其中一种距量趋于无穷，则Ln满足具有特殊标准差σ的高斯分布。

由于f（θ）＝sin2θ且f（φ）＝1／2π，每次碰撞后的lx总可以表示为lx＝dtanθcosφ。因此可得d lx＝dcosφcos－2θdθ，以及dθ＝1／（dcosφ）cos2θd lx。由f（θ）＝sin2θ和∫f（lx，φ）d lx＝∫f（θ）dθ，可得：

当，则θ→π／2，sinθ→1，同时cosθ→arctanθ，可得：

最后

式（3－36）说明当时，f（lx）→l－（μ＋1）x，其中μ＝2。这种情况下，〈l2x〉趋向无穷大。根据中心极限定限，当μ＝2时，

此时，x方向的横向扩散位移，即Ln，满足方差σ2＝n ln n的特殊高斯分布，即：

式中，α和β分别为归一化常量和校正系数，其中β由f（lx）的具体分布决定。可见，尽管二次电子逸出角度的概率分布并不均匀，但其横向扩散的概率分布总体上仍呈现高斯分布，而其标准差是碰撞次数的函数。

当SEY≠1时，二次电子的横向扩散理论上需用Branching Levy漫步模型进行分析。图3－8（b）给出了SEY＝1.28时的二次电子横向扩散的模拟计算。当单个电子的碰撞统计上可以导致多个二次电子逸出时，总的二次电子数量将随碰撞次数指数增长。但由于每个二次电子的逸出速度和角度均遵守相同的、在导体平面各向同性的随机分布，因此对于指数增长的大量二次电子，向某一方向（如x方向）扩散某一距离的二次电子数量与向相反方向（如－x方向）扩散相同距离的二次电子数量概率上相同。因此可以判断，SEY＞1时，二次电子的Branching Levy漫步与SEY＝1时的随机漫步将满足相同的概率密度分布f（Ln）。

为验证以上结论，本节沿用图3－7所示的模型，计算一个初始电子分别在SEY＝1的随机漫步假设、以及SEY＝1.28的Branching Levy漫步假设下经过40次碰撞后的横向扩散。为得到准确的概率分布曲线，将上述过程分别重复40 000次和40次，并根据计算数据进行概率统计，得到了相应的概率密度拟合曲线。需要注意的是，对于SEY＝1.28的Branching Levy漫步，40次碰撞将会产生比40 000次随机漫步更多的二次电子数量，足以保证所得概率密度拟合曲线的准确性。图3－9给出了由式（3－38）计算的概率密度曲线（绿色实线），以及随机漫步（蓝色十字）和Branching Levy漫步（红色圆圈）相对应的拟合曲线。其中，式（3－38）中的系数α＝0.017 6及β＝0.66由随机漫步的数据标定。由图3－9可见，随机漫步和Branching Levy漫步的概率密度拟合曲线与理论曲线相互符合得很好。

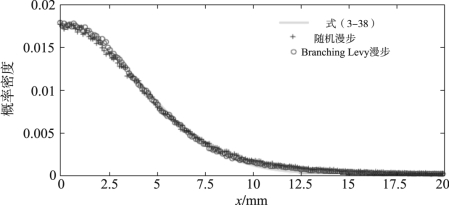
图3－9　随机漫步和Branching Levy漫步的拟合与对比［7］（见彩插）

需要说明的是，尽管本节中仅选取了1和1.28两个SEY值进行分析，但所得式（3－38）适用于任意SEY值的微放电过程。在常用SEY模型中，SEY的值大体介于0～2.2。其中，SEY＜1意味着电子的吸收，不足以维持随机漫步，因而不在本节讨论范围以内；SEY＝1意味着二次电子数量的零增长，对应随机漫步情形；SEY＞1意味着二次电子数量的指数增长，对应Levy Walk情形。当SEY＞1时，不同的SEY值仅引起所推导横向扩散概率密度函数常数项的变化，因此SEY在1～2.2之间任意取值，对于研究结论没有影响。本节中SEY取值1.28，是综合考虑了计算容量、碰撞次数和二次电子数量等方面的因素。对于概率密度的仿真分析而言，碰撞次数和二次电子数量越多，所得概率密度分布越准确；但对于Levy Walk，由较大的SEY数值引起的指数增长会很快耗尽计算机内存，并且只能得到较少的碰撞次数。1.28的取值是在扫描了多个SEY数值之后，选择了在现有计算条件下能够得到最多碰撞次数和二次电子数量时的SEY值。

根据式（3－38），可以继续完成矩形波导TE10模式下多载波微放电过程的理论计算。为验证式（3－38）的准确性，本节同时利用商用软件CST Particle Studio中的粒子模拟功能进行了同一矩形波导微放电过程的仿真。计算和仿真中所用的矩形波导模型，其宽度定为与标准波导WR229相同的58.17 mm，另外设定其高度d为0.43 mm、长度为100 mm。选择0.43 mm的高度是为了使得微放电更容易发生，从而减少粒子仿真所需的时间。对于上述矩形波导，在2.58～5.16 GHz频率范围内只有TE10模式可以被激励。为了方便进行结果的比较，我们采用与文献［5］相同的6路多载波信号。各个载波频率分别为3.57 GHz、3.67 GHz、3.77 GHz、3.87 GHz、3.97 GHz和4.07 GHz，场强均为70 000 V／m。最后，我们假设矩形波导内腔表面镀银，粒子仿真和理论计算中采用的SEY模型均为标准银表面边界的Furman模型［10］。

在理论计算中，将半余弦分布的TE10模式电场等间距分为11个区域，如图3－7（b）所示。在每一个区域中，二次电子随时间积累的数量可根据文献［5］中提出的统计理论进行计算。

在计算过程中，将多载波信号的时间周期等距离分为20个时间片段，并在每个时间段的结尾，根据式（3－38）提供的概率密度函数计算每个区域的二次电子横向扩散，然后将所有区间的电子数量累加，得到波导腔体内总的二次电子分布。上述计算过程与文献［5］完全相同。

为了分析初始电子数量对理论计算的影响，我们在计算中设置初始电子数分别为1、5、11和15，并沿x方向均匀分布在矩形波导中间的子区域内。图3－10（a）为二次电子累积的理论计算和粒子仿真结果的对比图，其中蓝色点划线为粒子仿真结果，其他曲线分别代表初始电子数为1、5、11和15的理论计算结果。为了方便比较仿真和理论计算结果的累积趋势，对图3－10（a）中的曲线进行了低通滤波，所得结果见图3－10（b）。

图3－10　微放电的粒子仿真和理论计算结果［7］（见彩插）

（a）低通滤波前；（b）低通滤波后

可以明显看出，当二次电子数量累积较大时（如20 ns以后），图3－10中的粒子仿真和理论计算曲线具有相近的斜率。其中，当初始电子数大于10、二次电子数量足够多时，理论计算曲线接近重合，且与仿真曲线几乎平行。其中，20 ns后初始电子数为15的理论计算曲线斜率角约为12.35°，仿真曲线的斜率角约为12.26°，两者之差小于0.8%。与发生在单个多载波包络周期内的“Single－event”微放电不同，多个包络周期微放电缘于多个多载波包络周期中剩余二次电子累积引发的放电，其放电阈值取决于不同多载波初始相位配置条件下二次电子的累积趋势。因此，由于初始电子数量及设置方法不同造成的粒子仿真与理论计算在总二次电子数量上的差别并不重要。

以上结果有效地验证了由式（3－38）描述的二次电子横向扩散概率密度函数的准确性。与此同时，由图3－10中亦可以看出初始电子数量对理论计算结果的影响。上述影响表明，将矩形波导划分为11个计算区域不够多。此时，尽管各个区域内的电场可以视为均匀场，但区域的空间尺寸对于二次电子的横向扩散仍然较大。增加初始电子数，相当于等效地加密了二次电子交换的区间，从而提高了二次电子横向扩散累积计算的精确度。与文献［5］中给出的相同间隙平行平板和多载波配置条件下均匀场中的结果相比，图3－10中二次电子增长速度相对较为缓慢，清楚地体现了TE10模式的非均匀场对多载波微放电中二次电子横向扩散的影响。

本节基于随机漫步和Branching Levy漫步模型，提出了一种分析非均匀场下大功率微波部件中多载波微放电过程的概率方法，严格推导了微放电过程中二次电子在平行金属表面间横向扩散的概率密度函数。基于所得的概率分布，本节给出了TE10模式矩形波导中多个包络周期多载波微放电过程中二次电子累积的纯理论计算演示，所得结果与采用商业粒子仿真工具所得结果相符合。