例8.17 众所周知血液中酒精浓度高会影响驾驶员的驾车能力，从而引发交通事故。《交通法》规定驾驶员血液中酒精浓度达20mg／100mL至80mg／100 mL为饮酒驾车，酒精浓度超80mg／100mL为醉酒驾车。但是血液中酒精浓度不是一成不变的。有一种药物动力学模型指出：一般人较长时间（例如一周以上）未饮酒可使血液中酒精浓度几乎为0，饮酒后血液中酒精浓度随时间的变化规律是
其中，c是酒精浓度（因变量），单位是毫克／升；t是时间（自变量），单位是小时；a，b，d是待定正参数，它们由该人的生理指标和饮酒量决定。由于存在种种其他因素的影响，具体血液中酒精浓度模型应当改为
其中，ε是随机误差，通常假设
某人一周内未饮酒，某时间饮酒后在不同时刻测量得血液中酒精浓度如表8-18所示。试确定关于该人的a，b，d的值，并判断他饮酒后多长时间再驾车，才有95%的概率不属于饮酒驾车。
表8-18 某人的血液酒精浓度数据
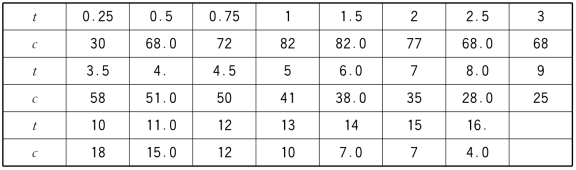
和线性回归情况相同的是，这儿也要从已知观测数据出发估计参数（a，b和d），从而得到经验回归方程；和线性回归情况不同是，线性回归模型中待估参数总是和自变量（或其平方、立方等）相加或相乘，称线性回归的待估参数是线性出现的，而式（8-3）中待估参数b和d出现为指数，不是线性出现的，这样的统计模型称为非线性回归模型。非线性回归模型的计算和线性回归模型大不一样。后文将算出估计值a=114.4，b=0.1853，d=1.9716，从而可以得到该人血液中酒精浓度的经验公式为
7.1.1节已根据经验公式画出图形，当时认为饮酒9.5小时后可以驾车。但是实际血液中酒精浓度的分布带有随机性，应当还需要进一步考虑：饮酒后多少小时驾车，才能有95%的可能性不会被判为饮酒驾车，即只有不到5%的可能性会被判为饮酒驾车。
许多实际问题和例8.17一样，待定参数不全以线性形式出现，这样的回归模型称为非线性回归模型。
许多经济模型都是非线性回归模型。例如：
Logistic模型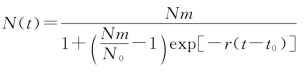
Gompertz模型 y=aexp（-exp（β-γx））+ε
Richards模型 y=（1+exp（β+γx））1／δ+ε
线性回归模型中待估参数个数等于自变量个数+1，而非线性回归模型中待估参数个数则与自变量个数无关，如例8.15中自变量只有1个，即t，而待估参数却有3个。
非线性回归模型的一般表达式是(www.xing528.com)
其中，x1，…，xp是自变量；b0，b1，…，bk是未知参数；f（x1，…，xp，b0，b1，…，bk）称为确定性部分，b0，b1，…，bk不全是以线性形式出现；ε是随机变量，有Eε=0，Var（ε）=σ2。当观测次数n不是太大时，假设ε服从正态分布。
若令
非线性回归模型可写为
非线性回归分析和线性回归分析的计算有两点相似：①通过对自变量和因变量的多次观测（表8-18），设法估计出非线性回归模型的参数；②常常通过最小二乘法，即使得
最小，从而估计β的值。对于例8.17，即令
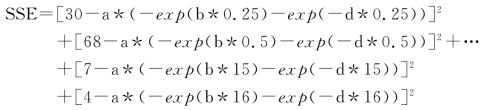
当选定某个参数a，b，d，使SSE=∑（yi-f（xi，β））2达到最小值时，参数a，b，d的值就是所需估计值。
非线性回归分析和线性回归分析之间的不同点之一是：由于待估参数中有些是以非线性形式出现，一般对于式（8-5）求最小值没有式（8-2）那样的公式可用，因而计算起来特别麻烦。所用的方法是非线性最小二乘法，即用最优化方法选择合适的β使残差平方和最小。
有时也用LAD（Least Absolute Deviation）方法即最小一乘法估计参数，就是选择合适的参数使
达到最小值，从而估计参数。这种得到参数估计值，从而得到经验回归方程的方法称为LAD回归。
式（8-5）中的SSE和式（8-6）中的S（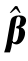
）称为目标函数，非线性最小二乘法和非线性最小一乘法都是通过最优化理论使目标函数最小，从而得到参数的估计值。
最优化的理论和方法非常丰富复杂，有多种最优化方法（使目标函数极小的方法），本书不可能细述最优化原理和算法，感兴趣的读者们可以阅读陈宝林的书［6］和其他有关最优化的文献，最优化也称为优化。但无论采用哪种最优化方法，都必须从一个预先给出参数的初始估计出发；经过多次迭代，每次迭代都改善参数估计值，从而使目标函数变小（如图8-8，仅考虑1个待估参数）。图8-8中，初估计是1.56，经过1次迭代，参数估计改善为2.5；经过第2次迭代，参数估计改善为1.9；经过第3次迭代，参数估计值改善为2.36；经过第4次迭代，参数估计改善为最优值2.2，这时目标函数经过4次下降达到最小值。可以得到参数的近似最优估计，即非线性最小二乘的最优解。由于最优化原理复杂，编程麻烦，最好调用SAS过程来计算。对于一个目标函数SAS有多种数学方法实施最优化，8.2.2重点介绍nlin过程的使用方法，8.2.4重点介绍nlp过程的用法。
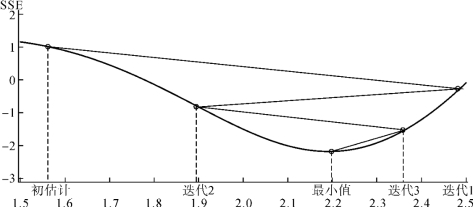
图8-8 优化过程示意图（只画出一元函数优化过程）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
