离散数学上册范式及主范式介绍

由上节可知，一个公式，在等价意义下，可以有许多种不同的写法，反过来说，几个形式上不同的公式完全可能是同一个公式（在等价意义下）。那么，在一个公式的诸多表示形式中，有没有一种标准形式呢？更进一步说，有没有一种标准形式是一个公式的唯一表示形式呢？回答是肯定的，这就是将要介绍的范式和主范式的概念。

定义1 原子或原子的否定称为文字；有限个文字的析取式称为一个子句；有限个文字的合取式称为一个短语。

例如，P，」P是文字；P∨Q∨」Q∨」R是一个子句；P∧」P∧R∧Q是一个短语。

特别地，一个文字既可以称为一个子句，也可以称为一个短语。

定义2 有限个短语的析取式称为析取范式；有限个子句的合取式称为合取范式。

例如，（P∨」Q）∧（」P∨」Q∨R）是合取范式，（」P∧Q）∨（P∧」R）∨（」Q∧R）是析取范式。

特别地，一个文字既可以称为一个合取范式，也可以称为一个析取范式。一个子句，一个短语可以看作是一个合取范式，也可以看作是一个析取范式。

例如，」P∨Q∨R既可说成是析取范式，也可说成是合取范式，文字P既可说成是合取范式，也可说成是析取范式。

定理1 对于任意公式，都存在等价于它的析取范式和合取范式。

证明 对于任意公式G，通过如下算法可得出等价于G的范式：

第一步，使用基本等价式，将G中的逻辑联结词→，↔删除。

第二步，使用」（」A）⇔A和德·摩根律，将G中所有否定词」移至原子之前。

第三步，反复使用分配律，即可得到等价于G的范式。证毕。

例1 将」（P∨Q）⇆（P∧Q）化为析取范式和合取范式。

解 因为有公式A⇆B⇔（A∧B）∨（」A∧」B），故」（P∨Q）⇆（P∧Q）⇔（」（P∨Q）∧（P∧Q）∨（（P∨Q）∧」（P∧Q）⇔（」P∧」Q∧P∧Q）∨（（P∨Q）∧（」P∨」Q）⇔（」P∧」Q∧P∧Q）∨（P∧」P）∨（Q∧」P）∨（P∧」Q）∨（Q∧」Q）为析取范式。

因为有公式A⇆Q⇔（A→B）∧（B→A），故」（P∨Q）⇆（P∧Q）⇔（」（P∨Q）→（P∧Q））∧（（P∧Q）→」（P∨Q））⇔（（P∨Q）∨（P∧Q））∧（」（P∧Q）∨」（P∨Q））⇔（P∨Q∨P）∧（P∨Q）∧（（」P∨」Q）∨（」P∧」Q））⇔（P∨Q）∧（」P∨」Q）为合取范式。

可见，给出一个公式G，它的范式不是唯一的，但是它有唯一的表示形式，那就是下面要介绍的主范式概念。

在介绍主范式概念之前，我们先介绍命题逻辑的一个重要性质——对偶性质。

在有关∨和∧的基本等价式中，不难发现如下一个现象：即它们都是成对出现的。例如，有G∨G⇔G，就有G∧G⇔G；有G∨（G∧H）⇔G，就有G∧（G∨H）⇔G。这些成对出现的等价式有如下一个特点：只要将一个等价式中的符号∨换成符号∧，将符号∧换成符号∨，其他符号（原子符号和否定符号」）不变，就能得到另一个等价式，这样成对的等价式，就互称为对偶式。

对偶式的一般说法是：在一个不含联结词→和⇆的公式里，将∧换成∨，∨换成∧，T换F，F换T，得一新公式，称为原公式的对偶式。

将一个等价式的等价号两端换成其对偶式，得一新等价式，称为原等价式的对偶式。

例2 写出下列表达式的对偶式。

(1)(P∨Q)∧R;

(2)(P∧Q)∨T;

(3)」(P∨Q)∧(P∨」(Q∨」S))。

解 这些表达式的对偶式是：

(1)(P∧Q)∨R;

(2)(P∨Q)∧F;

(3)」(P∧Q)∨(P∧」(Q∧」S))。

例3 求等价式（P∨Q）∧」（」P∧」（Q∨R））∨」（P∨Q）∨」（P∨R）⇔（（P∨Q）∧（（P∨Q）∨（P∨R）））∨」（（P∨Q）∧（P∨R））的对偶等价式。

解 原等价式的对偶等价式为（P∧Q）∨」（」P∨」（Q∧R））∧」（P∧Q）∧」（P∧R）⇔（（P∧Q）∨（（P∧Q）∧（P∧R）））∧」（（P∧Q）∨（P∧R））。

命题逻辑中的对偶性质为：如果一个等价式是成立的，其对偶等价式也成立。

如果有一个关于某一等价式的推导过程，只需将该过程中的每一步都换成其对偶式，我们就能得到其对偶等价式的推导过程。例如

因此，正因为命题逻辑中有如此好的性质，在下面的讨论中，我们只要能证明一个等价式，另一个对偶等价式就不证自明了，有事半功倍之效。

下面介绍主范式使用的一个重要概念：

定义3 设P1，…，Pn是n个原子，一个短语如果恰好包含所有这n个原子或其否定，且排列顺序与P1，…，Pn的顺序一致，则称此短语为关于P1，…，Pn的一个极小项。

例如，对原子P，Q，R而言，P∧」Q∧R，」P∧」Q∧R，P∧Q∧R都是极小项，但是，P，」P∧Q不是极小项，而」P∧Q对原子P，Q而言是极小项。(www.xing528.com)

显然，对于n个原子P1，…，Pn而言，其不同的解释共有2n个，对于P1，…，Pn的任一个极小项m，2n个解释中，有且只有一个解释使m取1值。

例如，对P，Q，R而言，」P∧Q∧」R是极小项，解释（0，1，0）使该极小项取1值，其他解释都使该极小项取0值。

如果将真值1，0看作是数，则每一个解释对应一个n位二进数。

假设使极小项m取1值的解释对应的二进数为i，今后将m记为mi。

例如，对P，Q，R而言，」P∧Q∧」R是极小项，解释（0，1，0）使该极小项取1值，解释（0，1，0）对应的二进数是2，于是」P∧Q∧R记为m2。对P，Q，R而言，8个极小项与其对应的解释见表1：

表1

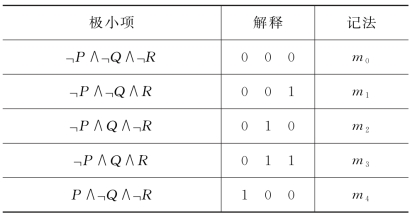
续表

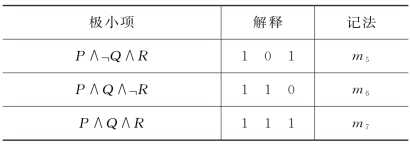
因此，一般地，对P1，…，Pn，2n个极小项为m0，m1，…，m2n-1。

下面给出主范式的概念。

定义4 设公式G中所有不同原子为P1，…，Pn，如果G的析取范式G′中的每个短语，都是关于P1，…，Pn的一个极小项，则称G′为G的主析取范式。

定理2 对于任意公式G，都存在等价于它的主析取范式。

证明 由定理1知，存在析取范式G′，使得G⇔G′。设G中所有不同原子为P1，…，Pn。对于G′中每一个短语G′i进行检查，如果G′i不是关于P1，…，Pn的极小项，则G′i中必然缺少某些原子Pj1，…，Pjk，而

于是，G′中非极小项G′i化成了一些极小项之析取。

对G′中其他非极小项也做如下处理，最后得等价于G的主析取范式。证毕。

在定理2的证明中，实际上已经给出了求公式的主析取范式的方法，例如：

G⇔」(R→P)∨Q∧(P∧Q)

⇔」(」R∨P)∨(Q∧P)

⇔(」P∧R)∨(Q∧P)

⇔((」P∧R)∧(Q∨」Q))∨((Q∧P)∧(R∨」R))

⇔(」P∧Q∧R)∨(」P∧」Q∧R)∨(P∧Q∧R)∨(P∧Q∧」R)

定理3 设公式G，H是关于原子P1，…，Pn的两个主析取范式，如果G，H不完全相同，则G，H不等价。

证明 因为G，H不完全相同，所以，或者G中有一个极小项不在H中，或者反之。不妨设极小项mi在G中而不在H中，于是，根据极小项的性质，二进数i所对应的关系P1，…，Pn的解释Ii，使mi取1值，从而使公式G取1值，Ii使所有不是mi的极小项取0值，从而使公H取0值，故G，H不等价。证毕。

定理3给出了判断两个公式是否等价的一个有效方法，只要求出两个公式的主析取范式，若它们相同，则两公式等价；若它们不同，则两公式不等价。

由定理2、3可立即得到如下定理。

定理4 对任意公式G，存在唯一一个与G等价的主析取范式。

求一个公式的主析取范式，还可以用真值表法，其步骤是：

（1）列出公式的真值表（表2）；

表2

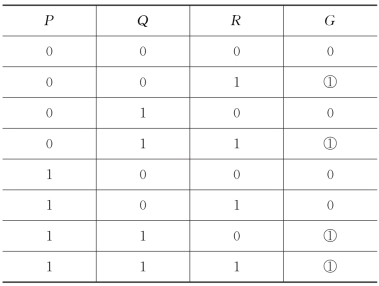
（2）将真值表最后一列中的1左侧的二进数所对应的极小项写出；

（3）将这些极小项析取起来。

例如，G⇔」（R→P）∨Q∧（P∨R）。

于是，G⇔（」P∧」Q∧R）∨（」P∧Q∧R）∨（P∧Q∧」R）∨（P∧Q∧R）。

根据命题逻辑的对称性质，不难给出主合取范式的概念，也不难得到和定理2、3、4相对偶的定理，请读者作为练习，自己给出。