在《高等数学》中曾经提到拉格朗日乘法，用来对等式约束优化问题的求解。实际上拉格朗日乘法在推广后可用于对不等式优化极值问题的求解，以解决不等式约束的非线性规划问题。
对于约束优化问题：
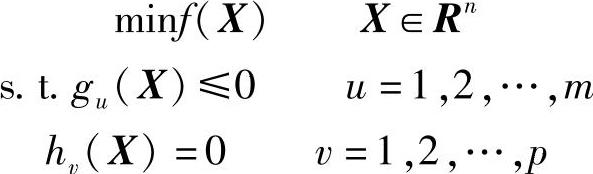
求解的实质是在所有约束条件形成的可行域内，求得目标函数的极值点即约束最优点。库恩-塔克（Kuhn-Tucker）条件（简称K-T条件）是非线性规划领域最重要的理论成果之一，通常用来判断和检验约束优化问题中的某个可行点是否为约束极值点，即将K-T条件作为确定一般非线性规划问题中某点是否为极值点的必要条件。对于凸规划问题，K-T条件同时也是一个充分条件。
对于一般约束优化问题，若X*是一个局部极小点，且各梯度矢量▽gu（X*）、▽hv（X*）组成“线性无关”的矢量系，那么必有一组非负乘子λu和另一组乘子μ使得下式成立：
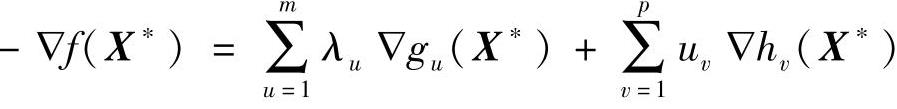
式中 m——在设计中的不等式约束面数；
p——在设计中点X*处的等式约束面数；
λu（u=1，2，…，m）——非负值的乘子，也称拉格朗日乘子。
K-T条件可阐述为：若X*是一个局部极小点，则该点的目标函数的梯度▽f（X*）可以表示为约束面梯度▽gu（X*）、▽hv（X*）的线性组合的负值。
gu（X*）在约束极值点X*处不起作用时，对应的λu一定为零，反之可以不为零。
对于凸规划问题而言，K-T条件不仅是确定约束极值点的必要条件，同时也是充分条件。凸规划问题有唯一的K-T点，但它所对应的拉格朗日乘子不一定是唯一的。
K-T条件的几何意义在于：如果X*是一个局部极小点，则该点的目标函数梯度▽f（X*）应落在该点诸约束面（所有起作用的约束条件）梯度▽gu（X*）和▽hv（X*）在设计空间所组成的锥角范围内。如图11-1所示，图11-1a中设计点X*不是约束极值点，图11-1b的设计点X*是约束极值点。
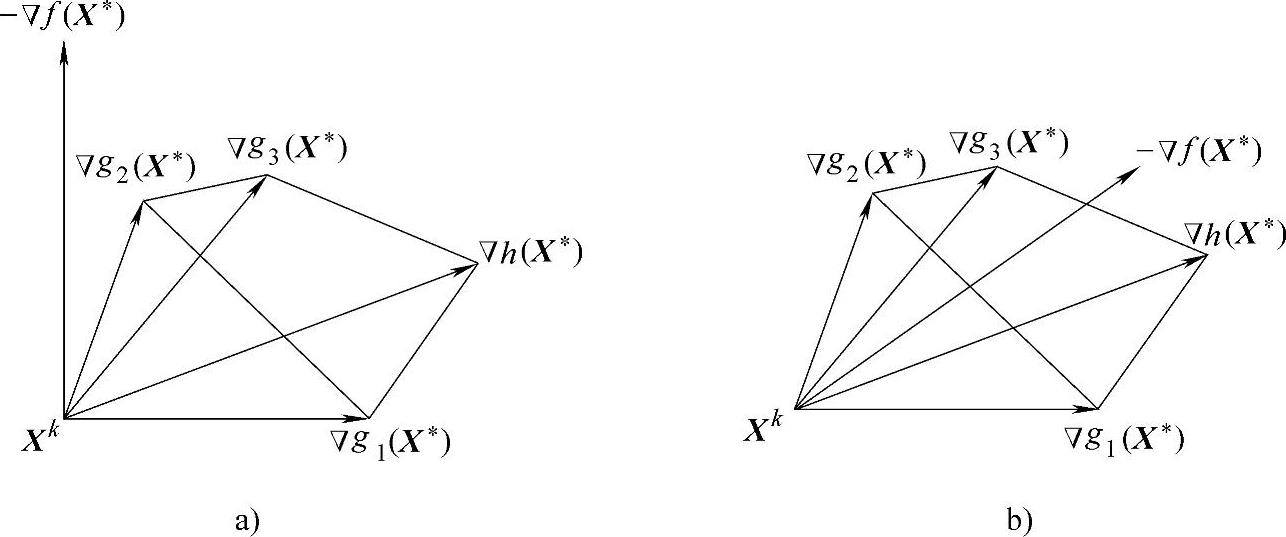
图11-1 K-T条件的几何意义
a）设计点X*不是约束极值点 b）设计点X*是约束极值点
现在通过图11-2所示的二维问题说明上述几何意义。图11-2表示在设计点Xk处有两个约束，且目标函数及约束条件均为凸函数的情况。图11-2a中，Xk点处目标函数的负梯度为-▽f（Xk）），两约束函数的梯度分别为▽g1（Xk）和▽g2（Xk），此时-▽f（Xk）位于▽g1（Xk）和▽g1（Xk）组成的锥角Γ之外，这样在Xk点附近的可行域内存在目标函数值比▽f（Xk）小的设计点，故点Xk不能成为约束极值点。图11-2b中，Xk点处的目标函数负梯度-▽f（Xk）位于锥角Γ之内，则在该点附近邻域内任何目标函数值比▽f（Xk）更小的设计点都在可行域之外，因而Xk是约束极值点，它必然满足K-T条件：
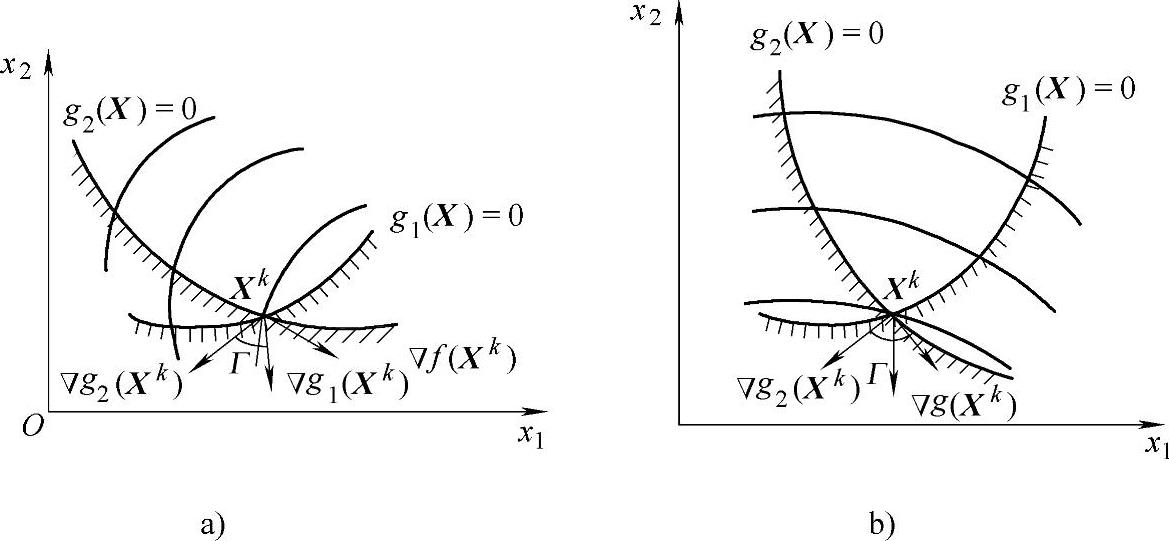
图11-2 约束极值点存在的条件
a）设计点Xk不是约束极值点 b）设计点Xk是约束极值点
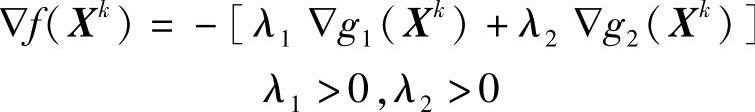
K-T条件主要应用于约束极值点问题的数值解法中，用以检验设计点Xk是否为约束极值点或局部最优点，并用以判断和消除那些不再起作用的约束条件，以保证在迭代中维持正确的起作用约束集合，对于目标函数和约束函数是凸函数的情况，符合K-T条件的点一定是全域最优点。(www.xing528.com)
例11-1 用“K-T条件”证明二维目标函数f（X）=（x1-3）2+x22在不等式约束：g1（X）=x21+x2-4≤0 g2（X）=-x2≤0，g3（X）=-x1≤0的条件下，在X*=[2，0]T为其约束极值点。
解：
1）作图求出：目标函数与约束函数的图像（见图11-3）。
2）求各函数在X*=[2，0]T处的梯度。
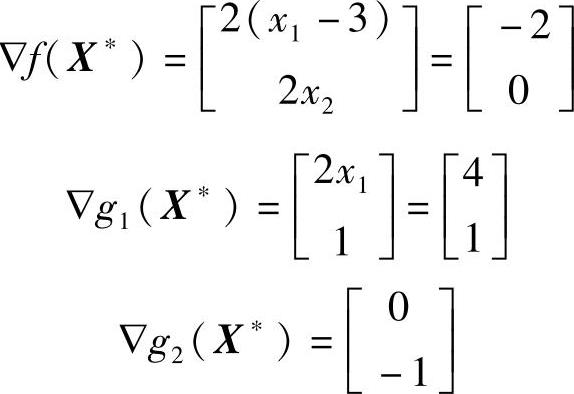
对于点X*而言，g1和g2→“适时约束”；g3→“非适时约束”。
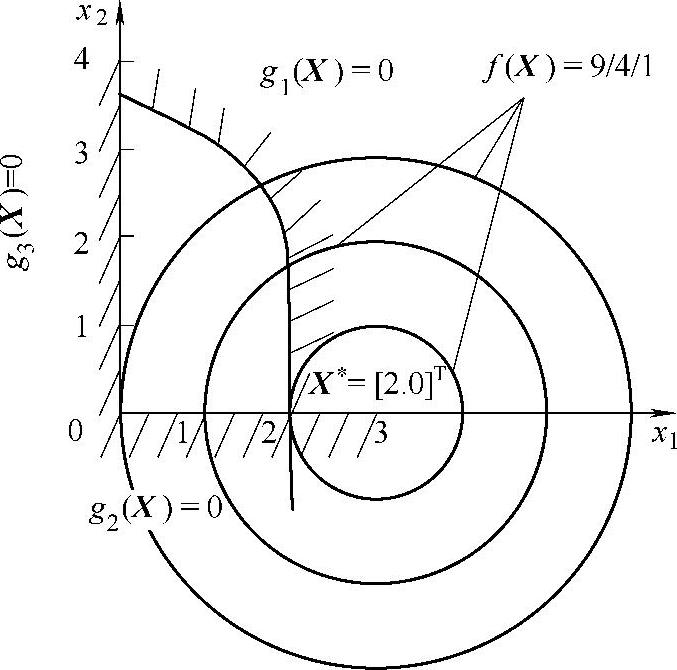
图11-3 例11-1目标函数与约束函数的图像
3）代入“K-T”条件。当非负乘子λ1=λ2=0.5时，“K-T条件”成立。故证X*为“约束极值点”。而且由于f（X）是凸函数，可行域是凸集，所以点X*为全局最优点。
例11-2 检验[1，5]T是否为以下问题的K-T点：
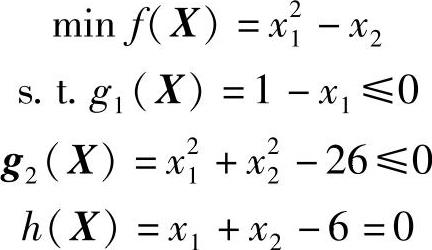
解：将x1*=1，x2*=5代入各约束条件检验，得g1（X）=0，g2（X*）=0，h（X*）=0，故在该点各约束条件均起作用。由图11-4可知，该点位于这些约束的交集。
因在该点处，目标函数梯度▽f（X*）=[2 1]T，各约束函数梯度▽g1（X*）=
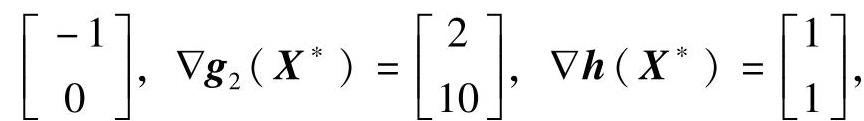
故K-T条件为
2-λ1+2λ2+μ1=0
-1+10λ2+μ1=0
设μ1=0，则λ1、λ2均大于零，故该点为K-T点。当然还可以找到大于或等于零的其他一组或几组λ值，能证明这一结论。所以，K-T点所对应的拉格朗日乘子的值不一定是唯一的。
另外，g1（X）=0和h（X）=0都是线性函数，而目标函数的黑塞矩阵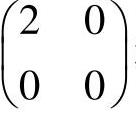
和g2（X）=0的黑塞矩阵
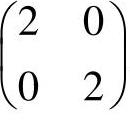又是半正定或正定，故原问题为凸规划，[1，5]T即为全局最优点。
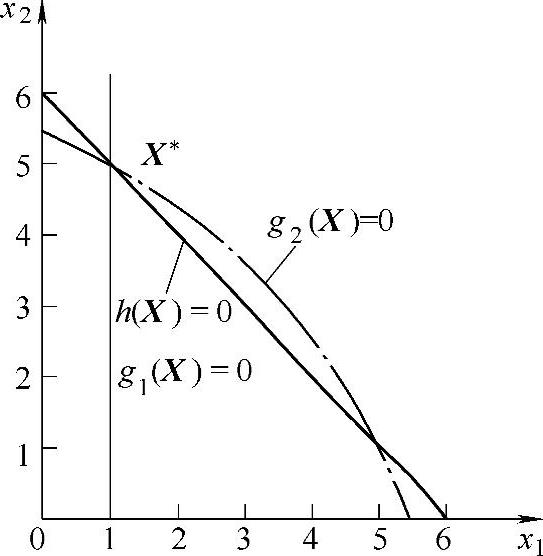
图11-4 例11-2图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
