正交多项式优化方法

11.1.1.1　Zernike多项式

Zernike于1934年提出了Zernike多项式。Zernike多项式在单位圆域内完备正交,采用其拟合面型时,各项系数相互之间不干扰,与采用的项数无关。由于Zernike多项式各项与像差的对应关系明确,所以它在光学设计和光学检测中都得到了广泛使用。此外,当前发展的针对自由曲面光学系统的矢量像差理论,都是针对面型中的Zernike项成分。因此,Zernike多项式是自由曲面光学系统设计时最重要的一种面型表达形式。Zernike多项式自由曲面的表征通常是在二次曲面的基础之上叠加Zernike多项式。也有光学设计者不使用二次曲面基底,而是直接采用Zernike多项式表征自由曲面,此时Zernike多项式中的旋转对称项与二次曲面等效。

Zernike多项式自由曲面的面型矢高可以表示为

式中,Zj是第j项Zernike多项式,cj是该项系数。Zj通常用极坐标函数表征,但可以与笛卡儿坐标系进行转换。

圆形孔径上的Zernike多项式常被分为两种形式:一种为Zernike标准多项式(ZEMAX中将其定义为Zernike standard polynomials,D.Malacara编著的Optical shop testing一书中将其定义为Zernike circle polynomials);另一种为Zernike条纹多项式(ZEMAX中将其定义为Zernike fringe polynomials,James C.Wyant在Basic wavefront aberration theory for optical metrology中将其定义为Zernike radial polynomials)。

两种类型的Zernike多项式虽然表达形式不完全一致,但它们具有相同的径向多项式:

式中,n-m≥0且为偶数,(ρ)可以看作是ρ的n级多项式,包含ρn,ρn-2,…和ρm项,(ρ)中ρ的多项式阶数的奇偶性与n或m的奇偶性相同。

Zernike标准多项式的表达形式为

式中,(ρ)前的系数可以有通用表达式[2(n-1)/(1+δm0)]1/2,其中δij是克罗内克函数,该系数的作用是对该项进行归一化处理。

Zernike条纹多项式的表达形式为

由此看出,Zernike标准多项式与Zernike条纹多项式的表达形式的区别是(ρ)前的系数。此外,两者多项式各项序号j的排序方式不同:Zernike标准多项式以n的大小依次排列,且cos项对应的j为偶数,sin项对应的j为奇数;Zernike条纹多项式以n+m的大小依次排列,且cos项排列在前,sin项排列在后。表11-1和表11-2分别列出了Zernike标准多项式自由曲面与Zernike条纹多项式自由曲面的初级像差项。

表11-1　Zernike标准多项式自由曲面的初级像差项(1～11项)

表11-2　Zernike条纹多项式自由曲面的初级像差项(1～9项)

Zernike标准多项式与Zernike条纹多项式的表达形式相似,但Zernike标准多项式具有归一化特性。W(ρ,θ)表示待拟合的曲面,Zj(ρ,θ)表示Zernike标准多项式,cj表示各项系数,(ρ,θ)表示用Zernike标准多项式拟合产生的自由曲面,那么有

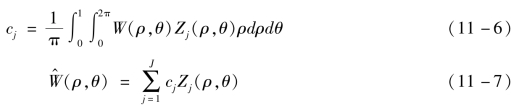
Zernike标准多项式的正交性是指

上式中的系数1/π由单位圆上的面积决定,即ρdρdθ=π。由于Z1(ρ,θ)=1,所以由式(11-8)可知,其他各项Zj≠1(ρ,θ)在圆形孔径上的平均值为0,所以对于整个自由曲面偏差的均值和标准差值有

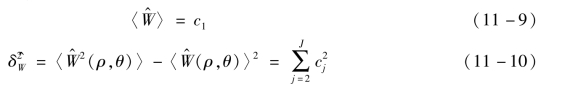
Zernike标准多项式自由曲面的正交性具有以下几个特点:

(1)采用不同项数的Zernike标准多项式对同一自由曲面进行拟合时,项数越多,拟合误差越小,但相同项对应的拟合系数相同,每一项系数之间的求解相互不干扰。

(2)常数项系数c1等于整个自由曲面偏差的平均值。

(3)j≥2的各项系数的平方和等于整个自由曲面RMS值的平方。

Zernike多项式的正交特性保证了自由曲面光学系统优化设计的效率。但Zernike多项式自由曲面由二次曲面基底叠加Zernike项的表达形式,使得难以从自由曲面项系数直观判断自由曲面与最佳拟合球面的偏差,不能在光学系统设计过程中兼顾自由曲面的可加工性和可检测性。

11.1.1.2　Q多项式

Q多项式自由曲面是美国QED公司的G.Forbes博士提出的一种新型的自由曲面表征形式,便于光学设计者在光学系统设计时,直接建立自由曲面项系数与该自由曲面偏差的关系。

Q多项式的提出首先被用于非球面,有Qcon和Qbfs两种非球面表征形式。前者称为强效非球面,用于描述非球面度较大的非球面面型;另一种称为温和非球面,用于描述非球面度不太大的非球面面型;。

Qcon非球面多项式定义了一个偏离二次曲面的非球面,矢高表达式为

Qbfs非球面多项式定义了一个偏离最佳拟合球面的非球面,矢高表达式为

式(11-11)和式(11-12)中,r=,u=r/rmax为归一化半口径,rmax为非球面的最大半口径;(u2)和(u2)均是m阶正交化雅可比多项式,am为多项式所对应的系数。

式(11-12)中第二项所描述的Qbfs非球面多项式,为该非球面与最佳拟合球面的z向偏差,考虑到z向偏差与法向偏差的转换,再对矢高的法向偏差求导,可以得到非球面的斜率表达式:

依据Qbfs非球面多项式的各项系数am可以直接计算出非球面斜率的RMS值。因此,在优化设计过程中,可以通过对各项系数am值的优化控制,实现非球面斜率的控制,从而在优化设计的过程中兼顾加工和检测的可行性。Qbfs非球面也称为斜率受控型Qbfs非球面。

在此基础上,通过引入含有(u2)cos mφ的对称函数项和(u2)sin mφ的非对称函数项,则构建了斜率受控型Qbfs自由曲面多项式表征:

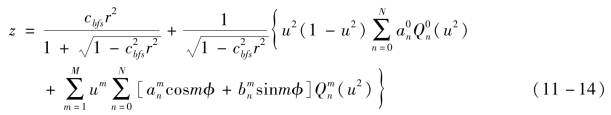
式中,φ为极坐标系中的极角;当m=0时,(u2)与(u2)是相同的;当m＞0且为整数时,(u2)用于表征沿着曲面法矢方向的偏差;为(u2)cos mφ对称函数项的系数,为(u2)sin mφ非对称函数项的系数。

令t=u2,(u2)=(t),与(t)相关联的雅可比多项式(t)为

式中,m＞0且为整数,n为非负整数,(t)多项式可见相关文献。

11.1.1.3　二维切比雪夫多项式

与Zernike多项式和Q多项式不同,二维切比雪夫多项式(2D Chebyshev Polynomials)是一种在方形区域内正交的多项式,可以用来描述方形孔径自由曲面的面型。(www.xing528.com)

二维切比雪夫多项式分别由x和y方向的一维第一类切比雪夫多项式相乘得到。x方向的一维第一类切比雪夫多项式Tn(x)在区间[-1,1]上相对于权重函数w(x)=1/正交,如式(11-16)所示:

前7项非归一化的一维第一类切比雪夫多项式Tn(x)如表11-3所示。

表11-3　前7项非归一化的一维第一类切比雪夫多项式

续表

将Tn(x)中的变量x替换为y即为y方向的一维第一类切比雪夫多项式,Tn(y)与Tn(x)具有相同的特性。由上述可知,正方形域(边长为2)的二维切比雪夫多项式Cj(x,y)为

式中,下标j为二维切比雪夫多项式的排序序号,为正整数;n和m为非负整数。二维切比雪夫多项式的正交特性为

式中,K为二维切比雪夫多项式归一化系数,取值如式(11-19)所示。

因此,归一化的二维切比雪夫多项式CNj为

前15项非归一化的二维切比雪夫多项式Cj(x,y)如表11-4所示。

表11-4　前15项非归一化的二维切比雪夫多项式

续表

11.1.1.4　二维勒让德多项式

二维勒让德多项式(2D Legendre Polynomials)也是一种在方形区域内正交的多项式,可以用来描述方形孔径自由曲面的面型。二维勒让德多项式的获得过程与二维切比雪夫多项式类似,也是由x和y方向的一维勒让德多项式相乘得到。x方向的一维勒让德多项式Pn(x)在区间[-1,1]上相对于权重函数w(x)=1正交,如式(11-21)所示。

前7项归一化的一维勒让德多项式Pn(x)如表11-5所示。

表11-5　前7项归一化的一维勒让德多项式

对于y方向的一维勒让德多项式,将Pn(x)中的变量x替换为y,即为Pn(y),Pn(y)与Pn(x)具有相同的特性。由上述可得,正方形域(边长为2)的二维勒让德多项式Lj(x,y)为

式中,下标j为二维勒让德多项式的排序序号,为正整数;n和m为非负整数。二维勒让德多项式的正交特性为

前15项二维勒让德多项式如表11-6所示。

表11-6　前15项二维勒让德多项式

11.1.1.5　非圆域的正交多项式

除了常规的圆形和方形孔径的自由曲面,在实际工程应用中,非圆形孔径光学元件的使用越来越多。对于此类非圆形口径的元件,圆域正交多项式失去了其正交特性。对于规则类型的方形、椭圆形、环形、六边形或扇形孔径等,可以采用格林姆-施密特正交化法(Gram-Schmidt Orthogonalization)获得所对应孔径上的解析正交多项式。

格林姆-施密特正交化法是以一组完备的多项式函数作为基函数,通过迭代变换,得到所对应孔径形状上的解析正交多项式。因为Zernike标准多项式广泛应用于面型和波前分析,而且在单位连续圆域内具有正交完备性,所以通常将Zernike标准多项式作为基函数。通过格林姆-施密特正交化法得到相应非圆域孔径上的解析正交多项式,具体过程如下。

为简便起见,将直角坐标系表示的Zernike标准多项式Zj(x,y)简写为Zj,其中下标j为正整数,从1开始,为Zernike标准多项式的排序序号。同样,Fj为相应非圆域孔径上的解析正交多项式,Gj为中间转换多项式,用于实现格林姆-施密特正交化过程。通常对于第一项常数项有

G、Z和F满足递推关系:

那么相应非圆域孔径的归一化正交多项式F为

式(11-25)中变换系数cj+1,k为

其中,A为内切于单位圆域的规则非圆形孔径的面积。

对于内切于单位圆域的规则非圆形孔径如环形、正方形、矩形、六边形和椭圆形等的面积AAA、ASA、ARA、AHA和AEA分别如下:

式(11-28)中,ε为环形孔径的遮拦比;式(11-30)中,a为矩形孔径沿X轴方向的半宽度,沿Y轴方向的半宽度为　;式(11-32)中,b为椭圆形孔径沿Y轴方向的椭圆半短轴,沿X轴方向的椭圆半长轴为单位1。

根据上述格林姆-施密特正交化法,通过迭代递推公式,可以获得相应规则非圆域孔径的解析正交多项式。此类非圆域正交多项式是以Zernike标准多项式为基函数变换得到的,在相应孔径上,对应的解析正交多项式具有与Zernike标准多项式相似的像差特性,它们分别可以用于相应孔径形状的自由曲面表征、拟合与分析等。