高一数学：函数单调性与奇偶性

【教学目标】

1．了解函数的单调性和奇偶性的概念，掌握有关证明和判断的基本方法．

（1）了解并区分增函数，减函数，单调性，单调区间，奇函数，偶函数等概念．

（2）能从数和形两个角度认识单调性和奇偶性．

（3）能借助图象判断一些函数的单调性，能利用定义证明某些函数的单调性；能用定义判断某些函数的奇偶性，并能利用奇偶性简化一些函数图象的绘制过程．

2．通过函数单调性的证明，提高学生在代数方面的推理论证能力；通过函数奇偶性概念的形成过程，培养学生的观察，归纳，抽象的能力，同时渗透数形结合，从特殊到一般的数学思想．

3．通过对函数单调性和奇偶性的理论研究，增学生对数学美的体验，培养乐于求索的精神，形成科学，严谨的研究态度．

【教学建议】

知识结构

（1）函数单调性的概念．包括增函数、减函数的定义，单调区间的概念函数的单调性的判定方法，函数单调性与函数图像的关系．

（2）函数奇偶性的概念．包括奇函数、偶函数的定义，函数奇偶性的判定方法，奇函数、偶函数的图像．

重点难点分析

（1）本节教学的重点是函数的单调性，奇偶性概念的形成与认识．教学的难点是领悟函数单调性，奇偶性的本质，掌握单调性的证明．

（2）函数的单调性这一性质学生在初中所学函数中曾经了解过，但只是从图象上直观观察图象的上升与下降，而现在要求把它上升到理论的高度，用准确的数学语言去刻画它．这种由形到数的翻译，从直观到抽象的转变对高一的学生来说是比较困难的，因此要在概念的形成上重点下功夫．单调性的证明是学生在函数内容中首次接触到的代数论证内容，学生在代数论证推理方面的能力是比较弱的，许多学生甚至还搞不清什么是代数证明，也没有意识到它的重要性，所以单调性的证明自然就是教学中的难点．

教法建议

（1）函数单调性概念引入时，可以先从学生熟悉的一次函数，，二次函数．反比例函数图象出发，回忆图象的增减性，从这点感性认识出发，通过问题逐步向抽象的定义靠拢．如可以设计这样的问题：图象怎么就升上去了？可以从点的坐标的角度，也可以从自变量与函数值的关系的角度来解释，引导学生发现自变量与函数值的的变化规律，再把这种规律用数学语言表示出来．在这个过程中对一些关键的词语（某个区间，任意，都有）的理解与必要性的认识就可以融入其中，将概念的形成与认识结合起来．

（2）函数单调性证明的步骤是严格规定的，要让学生按照步骤去做，就必须让他们明确每一步的必要性，每一步的目的，特别是在第三步变形时，让学生明确变换的目标，到什么程度就可以断号，在例题的选择上应有不同的变换目标为选题的标准，以便帮助学生总结规律．

函数的奇偶性概念引入时，可设计一个课件，以y＝x2的图象为例，让自变量互为相反数，观察对应的函数值的变化规律，先从具体数值开始，逐渐让x在数轴上动起来，观察任意性，再让学生把看到的用数学表达式写出来．经历了这样的过程，再得到等式f（－x）＝f（x）时，就比较容易体会它代表的是无数多个等式，是个恒等式．关于定义域关于原点对称的问题，也可借助课件将函数图象进行多次改动，帮助学生发现定义域的对称性，同时还可以借助图象（如y＝2x＋1）说明定义域关于原点对称只是函数具备奇偶性的必要条件而不是充分条件．

【函数的奇偶性教学设计方案】

教学目标

1．使学生了解奇偶性的概念，回会利用定义判断简单函数的奇偶性．

2．在奇偶性概念形成过程中，培养学生的观察，归纳能力，同时渗透数形结合和特殊到一般的思想方法．

3．在学生感受数学美的同时，激发学习的兴趣，培养学生乐于求索的精神．

教学重点，难点

重点是奇偶性概念的形成与函数奇偶性的判断

难点是对概念的认识

教学用具

投影仪，计算机

教学方法

引导发现法

教学过程

一、引入新课

前面我们已经研究了函数的单调性，它是反映函数在某一个区间上函数值随自变量变化而变化的性质，今天我们继续研究函数的另一个性质．从什么角度呢？将从对称的角度来研究函数的性质．

对称我们大家都很熟悉，在生活中有很多对称，在数学中也能发现很多对称的问题，大家回忆一下在我们所学的内容中，特别是函数中有没有对称问题呢？

（学生可能会举出一些数值上的对称问题，x2＝4，x＝±2等，也可能会举出一些图象的对称问题，此时教师可以引导学生把函数具体化，如y＝x2和y＝x，y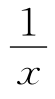＝等．）

结合图象提出这些对称是我们在初中研究的关于y轴对称和关于原点对称问题，而我们还曾研究过关于x轴对称的问题，你们举的例子中还没有这样的，能举出一个函数图象关于x轴对称的吗？

学生经过思考，能找出原因，由于函数是映射，一个x只能对一个y，而不能有两个不同的，故函数的图象不可能关于x轴对称．最终提出我们今天将重点研究图象关于y轴对称和关于原点对称的问题，从形的特征中找出它们在数值上的规律．

二．讲解新课

2．函数的奇偶性（板书）

教师从刚才的图象中选出y＝x2，用计算机打出，指出这是关于y轴对称的图象，然后问学生初中是怎样判断图象关于y轴对称呢？（由学生回答，是利用图象的翻折后重合来判定）此时教师明确提出研究方向：今天我们将从数值角度研究图象的这种特征体现在自变量与函数值之间有何规律？

学生开始可能只会用语言去描述：自变量互为相反数，函数值相等．教师可引导学生先把它们具体化，再用数学符号表示．（借助课件演示令x＝1，x＝－1比较f（1），f（－1）得出等式f（－1）＝f（1），再令x＝2，x＝－2，得到f（－2）＝f（2），详见课件的使用）进而再提出会不会在定义域内存在m，使f（－m）与f（m）不等呢？（可用课件帮助演示让x动起来观察，发现结论，这样的m是不存在的）

从这个结论中就可以发现对定义域内任意一个x，都有f（－x）＝f（x）成立．最后让学生用完整的语言给出定义，不准确的地方教师予以提示或调整．

（1）偶函数的定义：如果对于函数f（x）的定义域内任意一个x，都有f（－x）＝f（x），那么f（x）就叫做偶函数．（板书）

（给出定义后可让学生举几个例子，如y＝2x2，y＝x2－1，y＝｜x｜等以检验一下对概念的初步认识）

提出新问题：函数图象关于原点对称，它的自变量与函数值之间的数值规律是什么呢？（同时打出y＝x或y＝的图象让学生观察研究）

学生可类比刚才的方法，很快得出结论，再让学生给出奇函数的定义．

（2）奇函数的定义：如果对于函数f（x）的定义域内任意一个x，都有f（－x）＝－f（x），那么f（x）就叫做奇函数．（板书）

（由于在定义形成时已经有了一定的认识，故可以先作判断，在判断中再加深认识）

例1　判断下列函数的奇偶性（板书）

（1）f（x）＝－2x；

（2）f（x）＝｜x｜－2；

（3）f（x）＝；

（4）f（x）＝－x2，x∈［－3，1］；

（5）f（x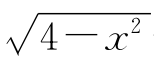）＝＋（x－2）2；

（6）f（x）＝2x－1．

（要求学生口答，选出1－2个题说过程）

解：（1）f（x）是奇函数．（2）f（x）是偶函数．

（3），∴f（x）是偶函数．

前三个题做完，教师做一次小结，判断奇偶性，只需验证f（x）与f（－x）之间的关系，但对你们的回答我不满意，因为题目要求是判断奇偶性而你们只回答了一半，另一半没有作答，以第（1）为例，说明怎样解决它不是偶函数的问题呢？

学生经过思考可以解决问题，指出只要举出一个反例说明f（x）与f（－x）不等．如f（－1）≠f（1）即可说明它不是偶函数．（从这个问题的解决中让学生再次认识到定义中任意性的重要）

从（4）题开始，学生的答案会有不同，可以让学生先讨论，教师再做评述．即第（4）题中表面成立的f（x）＝f（－x）不能经受任意性的考验，当x＝2时，由于2［－3，1］，故f（2）不存在，更谈不上与f（－2）相等了，由于任意性被破坏，所以它不能是奇偶性．

教师由此引导学生，通过刚才这个题目，你发现在判断中需要注意些什么？（若学生发现不了定义域的特征，教师可再从定义启发，在定义域中有1，就必有－1，有－2，就必有2，有，就必有－，有a就必有－a，从而发现定义域应关于原点对称，再提出定义域关于原点对称是函数具有奇偶性的什么条件？

可以用（6）辅助说明充分性不成立，用（5）说明必要性成立，得出结论．

（3）定义域关于原点对称是函数具有奇偶性的必要但不充分条件．（板书）

由学生小结判断奇偶性的步骤之后，教师再提出新的问题：在刚才的几个函数中有是奇函数不是偶函数，有是偶函数不是奇函数，也有既不是奇函数也不是偶函数，那么有没有这样的函数，它既是奇函数也是偶函数呢？若有，举例说明．

经学生思考，可找到函数f（x）＝0．然后继续提问：是不是具备这样性质的函数的解析式都只能写成这样呢？能证明吗？

例2　已知函数f（x）既是奇函数也是偶函数，求证：f（x）＝0．（板书）（试由学生来完成）

证明：

∵f（x）既是奇函数也是偶函数，

∴f（－x）＝f（x），且f（－x）＝－f（x），

∴f（x）＝－f（x）．

∴2f（x）＝0，即f（x）＝0．

证后，教师请学生记住结论的同时，追问这样的函数应有多少个呢？学生开始可能认为只有一个，经教师提示可发现，f（x）＝0只是解析式的特征，若改变函数的定义域，如f（x）＝0，x∈［－1，1］，f（x）＝0，x∈［－2，－1，0，1，2］，它们显然是不同的函数，但它们都是既是奇函数也是偶函数．由上可知函数按其是否具有奇偶性可分为四类

（4）函数按其是否具有奇偶性可分为四类：（板书）

例3　判断下列函数的奇偶性（板书）

（1）f（x）＝kx＋b（k≠0）；

（2）f（x）＝a（a∈R；

（3）

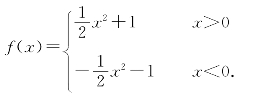
由学生回答，不完整之处教师补充．

解：（1）当b＝0时，f（x）为奇函数，当b≠0时，f（x）既不是奇函数也不是偶函数．

（2）当a＝0时，f（x）既是奇函数也是偶函数，当a≠0时，f（x）是偶函数．

（3）当x＞0时，－x＜0于是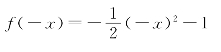

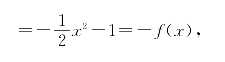
当x＜0时，－x＞0，于是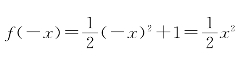＋1＝－f（x），

综上f（x）是奇函数．

教师小结（1）（2）注意分类讨论的使用，（3）是分段函数，当x＞0检验f（－x）＝－f（x），并不能说明f（x）具备奇偶性，因为奇偶性是对函数整个定义域内性质的刻画，因此必须x＞0，x＜0均有f（－x）＝－f（x）成立，二者缺一不可．

三、小结

1．奇偶性的概念(www.xing528.com)

2．判断中注意的问题

四．作业　略

五．板书设计

【习题精选】

一、选择题

（1）下列说法正确的是（　）．

（A）奇函数的图象一定过原点

（B）偶函数的图象一定与y轴相交

（C）y＝在其定义域内是增函数

（D）f（x）是奇函数的充要条件是它的图象关于原点对称

（2）下列函数中，在区间（0，2）上为增函数的是（　）．

（A）y＝－3x＋2

（B）y＝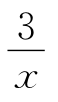

（C）y＝x2－4x＋5

（D）y＝3x2＋8x－10．

（3）函数f（x）＝x｜x＋px为常数），则（　）

（A）对任何常数p，f（x）是既不是奇函数也不是偶函数

（B）对任何常数p，f（x）是奇函数

（C）对任何常数p，f（x）是偶函数

（D）只有当p＝0时，f（x）是奇函数

【参考答案】

（1）D　（2）D　（3）B

二、填空题

（1）f（x）＝ax，g（x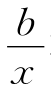）＝－在（－∞，0）都是减函数，则h（x）＝ax2＋bx在（0，＋∞）上是___________函数（填增或减）．

（2）函数f（x）＝2x2－mx＋3，当x∈［－2，＋∞）时，是增函数，当（－∞，－2］时是减函数，则f（1）___________．

（3）已知f（x）＝ax5＋bx3＋cx＋5（a，b，c是常数），且f（5）＝9，则f（－5）的值为___________．

（4）若函数f（x）＝x2－2（a－1）x＋2在（－∞，4］上是减函数，则a的取值范围是__________．

【参考答案】

（1）减　（2）13　（3）1　（4）a≥5

三、解答题

（1）断下列函数的奇偶性：

①

②

③f（x）＝｜x＋1｜－｜x－1｜；

④f（x）＝0，x∈［－6，－2］∪［2，6］；

⑤

（2）设f（x）在R上是奇函数，当x＞0时，f（x）＝x（1－x），试问当x＜0时，f（x）的表达式是什么？

（3）已知函数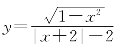，试判断函数的奇偶性，并加以证明．

（4）设函数f（x）与g（x）的定义域是x∈R且x≠±1，f（x）是偶函数，g（x）是奇函数，且，求f（x）和g（x）的解析式．

（5）若（m为常数）是奇函数，求m的值．

（6）若f（x）是偶函数，定义域为（－∞，＋∞），且在［0，＋∞）上是减函数，试比较与f（a2－a＋1）的大小．

【参考答案】

（1）①偶函数　②既不是奇函数也不是偶函数　③奇函数　④既是奇函数也是偶函数　⑤偶函数

（2）f（x）＝x（1＋x）

（3）奇函数

（4）

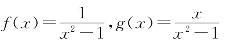
（5）－1

（6）当a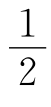＝时，f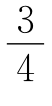（－＝f（a2－a＋1），当a≠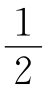时，f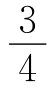（－＞f（a2－a＋1）．

【典型例题】

例1　给出下列函数的图象，指出函数的单调区间，并指明其单调性．

分析：通过图象直观观察其升降来判断其增减性，但必须注意区间端点的取舍要合理．

解：图（1）中f（x）的单调区间有（－3，］，（－1，0），［0，1），［1，3）．其中在（－3，1］和［0，1）上是减函数，在（－1，0）和［1，3）上是增函数．

图（2）中g（x）的单调区间有和，其中在和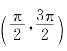上都是减函数．

说明：图（1）中x＝－3和x＝3不在定义域内，因此写单调区间时在这两个点上必须写成“开”而其余端点写成“开”或“闭”均可．图（2）中虽在两个区间上均为减区间，但不能把两个区间并起来．

例2　用函数单调性定义证明：

（1）为常数）在f（x）＝－2x2＋3x＋c（c为常数）在上是增函数．

（2）在在（－b，＋∞）上是减函数．

分析：虽然两个函数均为含有字母系数的函数，但字母对于函数的单调性并没有影响，故无须讨论．

证明：（1）设x1，x2是上的任意两个实数，且x1＜x2，

则

由x1＜x2得x2－x1＞0，由x1，得x1＜

2x2＜，2x2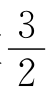＜，∴2（x2＋x1）＜3，即2（x2＋x1）－3＜0．

于是f（x1）－f（x2）＜0即f（x1）＜f（x2）．

∴f（x）在上是增函数．

（2）设x1，x2是（－b，＋∞）上的任意两个实数，且x1＜x2，

则

由x1＜x2得x1－x2＜0，由x1，x2∈（－b，＋∞）得x1＞－b，x2＞－b．

∴x1＋b＞0，x2＋b＞0．又a＞b＞0，∴b－a＜0，．

于是f（x1）－f（x2）＞0即f（x1）＞f（x2）．

∴在（－b，＋∞）上是减函数．

说明：由（1）中所得结论可知二次函数的单调区间只与对称轴的位置和开口方向有关，与常数c无关．若函数解析式是分式，通常变形时需要通分，将分子，分母都化成乘积的形式便于判断符号．

例3　函数f（x）＝（k2－3k＋2）x＋b在R上是减函数，求k的取值集合．

分析：首先需要对x前面的系数进行分类讨论，确定函数的类型，再做进一步研究．

解：当k2＋3k＋2＝0时，函数此时为f（x）＝b，是常数函数，在R上不具备增减性．

当k2－3k＋2≠0时，f（x）为一次函数，若在R上是减函数，则有k2－3k＋2＜0，解得1＜k＜2．故所求的取值集合为（1，2）．

说明：此题虽比较简单，但渗透了对分类讨论的认识与使用．

例4　下列函数是否具有奇偶性．

（1）f（x）＝3x3＋5x5；

（2）f（x）＝3x2－｜x｜＋1；

（3）f（x）＝－x2＋2，x∈（－2，2］；

（4）

分析：根据定义，检验f（－x）与f（x）的关系，同时注意定义域．

解：（1）f（－x）＝－3x3－5x5＝－f（x）．∴f（x）是奇函数．

（2）f（－x）＝3（－x）2－｜－x｜＋1＝3x2－｜x｜＋1＝f（x）．∴f（x）是偶函数．

（3）由于定义域（－2，2］不关于原点对称，故f（x）既不是奇函数也不是偶函数．

（1）f（x）的定义域为x∈R且x≠±1，是关于原点对称的，且有f（－x）＝f（x）和f（－x）＝－f（x）同时成立，故f（x）既是奇函数又是偶函数．