高中数学：待定系数法与数学归纳法

某些数学问题，如果所求结果具有某种明确的或者稳定的形式（待定结构），则可引进一些尚待确定的字符（待定系数）来表示这种结果，通过已知条件建立起关于待定系数的方程或方程组（个别时候也可能是不等式或者不等式组）.这样一来，问题就转换到这个稳定封闭的方程（组）系统之内，一切尽收眼底，解之即得待定系数，进而问题的待定形式便得以解决.

待定系数法在初等数学中有着广泛的应用，数列、三角与向量、求函数的解析式和曲线的方程等都会用到待定系数法.

待定系数法解题的关键是依据问题信息，明确所求元素的待定形式，选好待定系数，根据条件正确、简练地列出待定系数满足的方程或方程组，进而求解，最后确定问题的最终答案.这个过程简单来说就是四个字：设、列、解、答.

例1 人的最美身材应该符合黄金分割，即上身高度与下身高度之比等于下身高度与全身高度之比（下身高度为上身高度与全身高度的等比中项），该比值即为人体的黄金分割比，试求该比值.（下身与上身以肚脐为界）.

探究：如图所示，假设全身AB=1，下身OB=x（此时黄金分割比即为x），则上身OA=1-x.

由题意可得，解得，舍去负值，

最终黄金分割比为

说明：待定系数的选择也是有一定技巧的.请注意我们假设全身为1而不是a，这就在一定程度上简化了运算.另外，选择上身为x还是选择下身为x，也要体现结论和条件的双重要求.该题设下身为x，它与全身1之比还是x，问题便朝着确切的方向自动走去.

例1图

例2 零点的时候时针与分针是重合的，至少经过多少时间它们会再次重合起来？在此期间，时针所转过的角度是多少？24h之内，时针与分针重合多少次？

探究：分针速度为时针的12倍，分针和时针再次重合意味着它们产生了“套圈现象”.在此期间，分针比时针多转了一圈360°.

假设在此期间，时针所转过的角度为x，则分针的角度为12x，所以12x=x+360°，所以.360°对于时针可以折合时间12h，所以至少经过它们会再次重合起来.

例2图

观察时针和分针的转动过程时你会发现，几乎在任何两个相邻的整点之间，分针都会超越时针一次，完成一次重合，但是这个规律在11点以后发生了意外；从11点到12点再到13点这期间，它们只在12点整重合一次，所以24小时之内，时针分针完成了22次重合.

说明：依据时针分针的运动状态，从它们的速度和套圈现象出发，在这个稳定的封闭系统内引入待定系数，通过方程牢牢地构建起各种要素间的联系，解决这个系统内的问题便容易把握了.

例3 （1989年全国高考题）是否存在常数a，b，c，使得等式1·22+2·32+…+n（n+1）2=（an2+bn+c）对一切正整数n都成立？证明你的结论.

探究：这是一个开放性问题，如果存在，由已知等式对一切正整数n都成立，则n=1，2，3的时候，上述等式应该成立，这就可以列出关于a，b，c的方程组.若方程组有解，再用数学归纳法证明等式对所有正整数n成立.

整理得，解得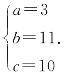

于是，对n=1，2，3，原等式成立，但是对于其他的正整数n，原等式是否成立？对此，我们只能依靠数学归纳法.

假设对n=k时等式成立，即1·22+2·32+…+k（k+1）2=（3k2+11k+10），

则n=k+1时，1·22+2·32+…+k（k+1）2+（k+1）（k+2）2

也就是说，原等式对n=k+1也成立.

综上所述，当a=8，b=11，c=10时，题设的等式对一切正整数n都成立.

说明：从特殊到一般，先猜想后证明，这完全符合我们的认知习惯.其中建立关于待定系数a，b，c的方程组至关重要.这是一个空前绝后的高考题，题型特征鲜明，问题设计极具想象力和创造性.

对于n=k+1的证明，一定要有目标意识，在归纳假设的条件下，明确结论的最终要求，有的放矢地进行推算.

从初中到高中，无论是求一次函数、二次函数、反比例函数的表达式，还是求直线、圆、椭圆、双曲线、抛物线的方程，往往只有一种方法——待定系数法.(www.xing528.com)

例4 与圆（x-2）2+y2=2相切，且在x轴与y轴上的截距相等的直线有（ ）.

A.1条 B.2条 C.3条 D.4条

探究：在坐标轴上截距相等的直线有两种：如果截距为零，则可设其方程的待定形式为y=kx；如果截距非零，则可以设其方程的待定形式为，即x+y-a=0（a≠0）.

因为圆心到切线的距离等于半径，所以，解得k=±1；或，解得a=0（舍去）或a=4.

所以所求的切线方程分别为y=x，y=-x，x+y-4=0，选C.

说明：本题也可以数形结合一下，画出图形，借助于圆心坐标与半径的特殊关系可以发现有多个等腰直角三角形，从中也可以发现问题的答案.但是，待定系数法才是通性通法，而且本题的计算也非常简练.

例5 （1993全国高考题）在面积为1的△PMN中，tan∠PMN=，tan∠MNP=-2.建立适当的坐标系，求以M，N为焦点且过点P的椭圆方程.

探究1：如图，以MN所在直线为x轴，MN的垂直平分线为y轴建立直角坐标系.设椭圆方程为，焦点为M（-c，0），N（c，0）.

例5图

由，tan（π-∠MNP）=2，可得直线PM和直线PN的方程分别为和y=2（x-c）.

将此二方程联立，解得，即P点坐标为

在△MNP中，|MN|=2c，MN上的高为点P的纵坐标，

所以

由题设条件S△MNP=1，所以，即P点坐标为

由两点间的距离公式：

得

又b2=a2-c2=

故所求椭圆方程为

探究2：同探究1，得，P点的坐标为

因为点P在椭圆上，且a2=b2+c2.将点P坐标代入椭圆方程可得：

化简得3b4-8b2-3=0，解得b2=3或（舍去），

故所求椭圆方程为

说明：本题用了两次待定系数法：第一次联立两条直线方程，求出点P的坐标；第二次是利用三角形的面积为1列出关于c的方程，解得c值和点P的坐标，最后的椭圆方程便唾手可得了.

请通过下面的分析，更好地把握待定系数法的关键环节。