地震荷载动力分析与工程结构可靠度设计原理

为了克服中心点法的不足，验算点法有以下两点改进：

（1）当极限状态方程为非线性曲面时，不以通过中心点（均值点）的切平面作为线性近似，而以通过失效面g（x）＝0上某一点P*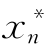＝[，，…，]T的切平面作为线性近似，减小中心点法的误差。

（2）考虑基本变量xi的实际分布类型。通过“当量正态化”把非正态变量在P*点处变换为当量正态变量，以考虑变量分布对可靠指标的影响。其中P*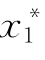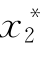（，，…，）称验算点。

1.验算点法基本公式

设结构极限状态方程为

式中，xi（i＝1～n）服从正态分布且相互独立。

引入标准化变量

将　

代入式（5-63）得

或　

图5-7　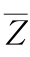＝0上的验算点P*

式（5-64）或式（5-65）为标准正态化空间内的极限状态曲面方程。验算点是_上一点，如图5-7所示。过P*作Z＝0的切平面方程（即在P*点展开为泰勒级数取至线性项）即

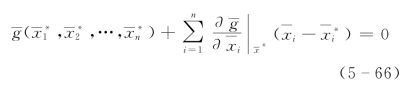
由于P*是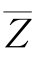＝0上的一点，因此

切平面方程成为

式（5-68）各项除以，则

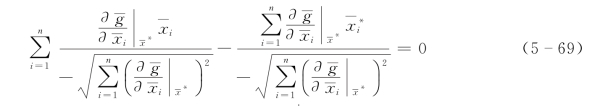
令　

则式（5-69）成为

式（5-72）为极限状态曲面＝0通过P*点的切平面方程的标准形式。其中d为标准正态空间原点至切平面的距离，β为可靠指标，αi为切平面法向矢量的方向余弦，也是矢量表示的d或β的方向余弦。

由于P*为切平面方程之切点，由β的几何意义知

因而αi不仅是的方向余弦，也是的方向余弦。由此可得验算点坐标与β关系为

将变回x空间，有

或　

注意到式（5-39）、式（5-40）、式（5-64）、式（5-65）可得

将式（5-77）代入式（5-70）得

式中　——验算点在原x空间中的坐标。

将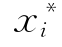代入式（5-63）得

式（5-76）、式（5-78）及式（5-79）即为验算点法方程组。它共有2n＋1个方程，可解出（i＝1～n）、αi（i＝1～n）及β共2n＋1个未知数。但由于一般式（5-79）为非线性函数，通常采用逐次迭代法解上述方程组。

2.当量正态化

上述可靠指标的计算方法适合于结构功能函数的基本变量均为正态分布情况。当其中任一变量xi为非正态分布时（如结构抗力、土料凝聚力一般为对数正态分布，地震荷载、风荷载、楼面活荷载一般为极值Ⅰ型分布），需首先将其当量正态化。

当量正态化的条件如图5-8所示，即

（1）在验算点处，当量正态化变量x＇i（均值，标准差）的分布函数与原随机变量xi（均值，标准差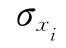）的分布函数相等。

（2）在验算点处，当量正态化变量x＇i的概率密度函数与原随机变量xi的概率密度函数相等。并由此确定当量正态变量的均值和标准差。

由条件（1）：，对x＇i标准化处理后得

图5-8　当量正态化条件

对Φ（·）求逆，得到

解出　

由条件（2）：，对于与式（5-80）相应的原函数求导，然后赋于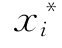点值，即

得到

解出　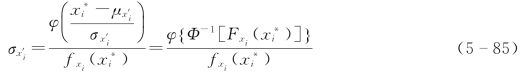(https://www.xing528.com)

式中　——表示[]内的函数对x＇i求导后再令x＇i＝；

——表示[]内的函数对xi求导后再令xi＝；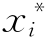

Φ（·）、Φ—1（·）——标准正态函数的分布函数和它的逆函数；

φ（·）——标准正态分布密度函数。

特殊地，当xi为对数正态分布时，求出如下：

对应于条件（1）：，有

将式（5-86）左边对x＇i求导后令x＇i＝，右边对xi求导后令xi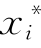＝，得到

由条件（2）知，式（5-87）等号两边的φ（·）相等，于是得到

又由条件（1）得

从而有　

解出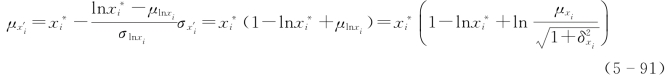　

式中　——对数正态分布变量xi的均值和变异系数。

3.验算点法计算步骤

一般地，当结构功能函数的基本变量为任意分布的独立随机变量时，按验算点法计算可靠指标β需逐次迭代，具体步骤为：

（1）列出极限状态方程g（x1，x2，…，xn）＝0，并确定所有基本变量xi的统计参数或。

（2）假定验算点和β的初值，一般取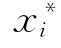初值为其均值，β初值取为0。

（3）对于非正态变量xi，由式（5-82）、式（5-85）计算当量正态变量的均值和标准差，并分别取代原变量的和。

（4）采用式（5-78）计算β的方向余弦（也称灵敏度系数）。

（5）计算的新值

或　

（6）按式求解β。

（7）重复（3）～（6）步，直至前后两次求出的β值在允许误差以内，此时的β、即为所求。

【例5-4】 设某钢梁承受确定性弯矩M＝128.8k N，钢梁截面的塑性抵抗矩ω和屈服强度f都是随机变量，用验算点法求解其可靠指标β。已知变量分布类型及统计参数为：抵抗矩ω：正态分布，μω＝884.9×10—6 m3，δω＝0.05；屈服强度f：对数正态分布，μf＝262×106 N/m2＝262MPa，δf＝0.10。

解：结构极限状态方程

Z＝g（x）＝ωf—M＝0

迭代一：

（1）假定初值。设β0＝0，则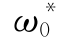＝μω＝884.9×10—6 m3，＝μf＝262MPa。

（2）当量正态化。对于对数正态变量f，求μ＇f、σ＇f。

由式（5-91）和式（5-88）有

μ＇f＝f*

＝262×106（1—ln262×106＋ln262×106—ln）

＝260.79（MPa）

σ＇f＝f*σlnf＝f*＝262×106

＝26.13（MPa）

（3）求方向余弦αi。

对于正态变量ω，其标准差σω在各迭代步中保持不变，即

σω＝μωδω＝884.9×10—6×0.05＝44.25×10—6（m3）

由式（5-78）有

（4）求新值（其中β为待求量）。

ω*＝μω＋αωβσω＝884.9×10—6—0.449×44.25×10—6β

f*＝μ＇f＋αfβσf＇＝260.79×106—0.895×26.13×106β

（5）求可靠指标β1。

由g（x*）＝ω*f*—M＝0有

（884.9×10—6—0.449×44.25×10—6β）（260.79×106—0.895×26.13×106β）—128.8＝0

解出　β1＝4.269

由于β1≠β0＝0，故需第二次迭代。

在第二次迭代中，以β1代替β0求得迭代二中验算点新值

＝μω＋αωβ1σω＝884.9×10—6—0.447×44.25×10—6×4.269＝800.68×10—6（m3）

＝μ＇f＋αfβ1σ＇f＝260.79×106—0.895×26.13×106×4.269＝160.86×106（N/m2）

重复（2）～（5）步，求得β2＝5.161。

由于β2≠β1＝4.269，仍需第三次迭代。重复迭代二步骤求得β3＝5.169。

由于β3≈β2＝5.161，停止迭代。这时计算结果为β＝5.169，ω*＝748.80×10—6 m3，f*＝172.01×106 N/m2。β迭代过程见表5-2。

表5-2　β的迭代求解过程