太阳能集热器导热问题的数理方程典型应用

对于平板型太阳能集热器，集热板的温度是关于x，t的二维变量，管内流体流动缓慢且流动距离较小，因此可认为在y方向集热板没有温度梯度（图1.2）。

图1.2　平板型太阳能集热器截面图

根据传热学中的定义，可以把肋片升温的过程视为准稳态的过程，根据对称性取宽为Δx、长为1m的集热板分析。因此根据能量守恒，单位时间内热量的吸收量为

Q1＝S·Δx

式中，S为单位时间内太阳的辐射强度。其中单位时间内其热量散失量为

Q2＝－UL×Δx（T－Ta）

式中，UL为系统的总热损系数。

对x方向，根据傅里叶导热定律可得

集热板吸热升温，可得

整理得

化简得

假设一平板式太阳能集热板，初始时刻集热板温度为Ta，管壁处的温度分布为f（t），集热板两管之间的距离为L，则问题转化为在区域t＞0，0＜x＜L中求解如下定解问题：

首先进行函数替换，令T＝Ta＋u（x，t）e－At，其中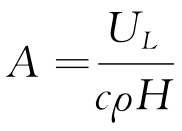，替换之后定解问题变为

根据解的叠加原理，上述定解问题的解可由齐次方程非齐次边界条件和非齐次方程齐次边界条件两个定解问题叠加而得，即定解问题

和定解问题

其中。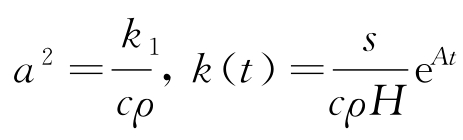

对定解问题（2），发现非齐次边界条件是关于时间的函数，因此将其齐次化。取U（x，t）＝φ（t），则U（x，t）满足

U（0，t）＝U（L，t）＝φ（t）

U（x，0）＝φ（0）

令u（x，t）＝U（x，t）＋v（x，t）代入原问题，则v（x，t）满足

根据解的叠加原理，上述定解问题的解可由齐次方程非齐次边界条件和非齐次方程齐次边界条件叠加而得，即定解问题

和定解问题

对定解问题（5）可以采用分离变量法求解，令

v（x，t）＝X（x）T（t）

则代入方程

XT′＝a2X″T

即

等式只有在两边均等于常数的时候成立，令此常数为－λ，则有

T′＋λa2T＝0

X″＋λX＝0

对第二个式子而言，应当满足边界条件(www.xing528.com)

v（0，t）＝v（L，t）＝0

即

X（0）＝X（L）＝0

（1）当λ＜0时，方程的通解为

令其满足边界条件，必须

满足条件只能C1＝C2＝0，因此λ＜0时无平凡解。

（2）当λ＝0时，方程的通解为

X（x）＝C1＋C2x

要满足边界条件，X（x）也恒为0。

（3）当λ＞0时，方程的通解为

由边界条件X（0）＝0知C1＝0，再由可知，若使上式成立，则必须，即

因此得到

将λ＝λk代入方程T′＋λa2T＝0中可得

因此得到一列可分离变量的特解

利用叠加原理构造级数形式的解

由于v（x，0）＝φ（x），因此将t＝0代入上述解中可得

进行傅里叶级数展开得

因此定解问题（5）的解为

对于定解问题（6），采取齐次化原理求解。

令t′＝t－τ，则定解问题（6）化为

由齐次化原理得定解问题（6）的解为

因此，根据叠加原理，定解问题（4）对应的解为

同理，定解问题（3）的解为

根据叠加原理，定解问题（2）对应的解为

定解问题（2）的解加定解问题（3）的解即为定解问题（1）的解：

代回T＝Ta＋u（x，t）e－At中得

将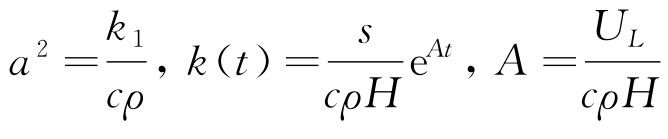，［g（x）－Ta］＝φ（x），［f（t）－Ta］eAt＝φ（t），μ（x）＝φ（x）－φ（0）＝g（x）－f（0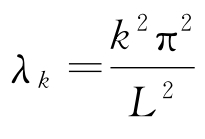），替换可得

化简得

经验算，该解满足方程的边界条件及初始条件。