我的数学课堂：深刻认识数学

我认为学习数学应当深刻理解数学问题的本质，重视数学思维的渗透、培养，重视掌握数学问题的基本研究方法。这就像是掌握了数学这把剑的“意”，就不必在意那些套路，因为总能看出题目的破绽。

（1）多问一个为什么。数学思维的提升，从有效的数学问题开始。不放过任何一个有效的数学问题，寻求每一个数学解法，甚至每一个步骤的合理性，对于入门级的学生来说，是提升数学思维的一个有效途径。我再以前面提到过的问题1 为例，来谈谈我的教学方法：

问题2：请作出函数的简图。

师：能否用初中学过的二次函数作图方法来作出f（x）的图像？

生：5 点法在这里不能用。

师：为什么不能用？（这个问题学生很难回答）如果非要用5 点法，你会选哪5 个点？为什么？

生：x=0，±1，±2。

师：为什么选这5 个点？

生：随便选的（奇函数通过原点，其他随便选）。

师：二次函数作图选了哪5 个点？为什么选这5 个点？

生：二次函数的顶点，还有对称的两组点，顶点决定了二次函数的最值，另外两组点确定了二次函数的形状（开口大小，“形状”叙述不正确，此时尚无法纠正）。

师：也就是说二次函数的5 点的确定，是基于二次函数的单调性、对称性分析后作出的。那么你认为对于一个完全陌生的函数，我随便选5 点画它的图像准确吗？那我多画几个点，10 个点？

生：不准确，点多不一定就有用。应该要先分析新函数的性质。

师：说得很好，我们借鉴二次函数的作图方法，不是照搬照抄，要学会其作图的合理性，学会5 点法背后所蕴含的真正的数学研究方法。那么你们能告诉我这个函数具有哪些典型的函数性质吗？

生：它是一个奇函数，因为对于定义域中的任意x，都有f（x）=f（-x）。

师：为什么要研究奇偶性？研究奇偶性给我们带来了什么好处？

生：函数关于原点对称，所以只需要研究［0，+∞）上函数的单调性就能知道函数整体的单调性。

师：怎么研究［0，+∞）上函数的单调性？

生：取0 ≤x1 ≤x2，则有

师：此处为什么要作差？为什么要进行因式分解？

生：作差是为了比较f（x1）和f（x2）的大小关系，根据定义来判断函数的单调性。因为最后要判断式子的正负号，所以因式分解后，我们可以根据各个因式的符号，了解整个式子的正负号。(www.xing528.com)

师：现在能判断式子的正负号了吗？

生：不能，说明［0，+∞）上函数不单调。

师：如何确定函数的单调区间？如何寻找一个区间，使得在这个区间上式恒为正或恒为负？

已经可以判断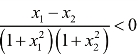，只需判断1-x1x2 恒为正或恒为负。也就是要寻找一个区间，使得在这个区间x1x2 ＞1 恒成立或x1x2 ＜1 恒成立，也就是x1x2 的最小值恒大于1 或最大值恒小于1。

生：有的，在（0，1）上，x1x2 的最大值恒小于1；在（1，+∞）上x1x2 的最小值恒大于1。所以我们可以认定函数f（x）在区间（0，1）上递增；在（1，+∞）上递减。

师：为什么不考虑x1 ＜1 ＜x2 的情况？

生：这样的x1、x2 不是在一个区间上任取的两个值。

……

限于篇幅，后面的讨论不再详述。在每一个关键问题上教师特意设问、引导，更严谨、细致的分析会使学生对于数学问题的认识更加深刻。常常有学生会问这样的问题，我上课都听得懂，但是题目不会做是什么原因？其实这就是学生能够明白解题的过程，而无法抓住解题的思路。强调解题思路，对每一个解题步骤多问一个为什么，剖析其背后的思考，是提高学生数学思维的有效途径。

（2）抓住问题的核心。抓住数学问题的核心本质不言而喻是一件十分重要的事，但是做起来很难。这要求教师对数学问题的认识深刻，数学功底深厚。那怎么算是抓住了问题的核心本质呢？以函数单调性的定义为例，我认为其中最难理解的是定义中采用二元变量及任意性，而大多数教师根据教学参考书只是强调了任意性，却忽视了变量为什么要用二元这一个问题。变量的个数（元）是代数的最基本问题之一。所以，我对函数单调性的课，必须从单变量能否刻画函数的单调性开始。我会设计以下问题：

①若对于定义域中的任意x 满足f（x+1）＞f（x），f（x）是否为增函数？

②若对于任意x ＞0 满足f（2x）＞f（x），f（x）在（0，+∞）上是否为增函数？

③若对于定义域中的任意x 满足f（x+t）＞f（x），t 为某个正常数，f（x）是否为增函数？

再如基本不等式的教学中，我会故意设计这样一个环节：

问题3：求证：a3+b3+c3 ≥ab+bc+ca。

这是一个错误命题。为什么是错误的？因为两边不齐次，基本不等式无法改变齐次式的次数。能否举出反例，注意到左边次数比右边高，故只需让a、b、c 取尽可能小的正数即可，如a=b=c=0.1。次数是代数中除变量个数（元）外的第二个最基本的问题。

数学问题的本质，即便是一本书也是写不完的，在此，我也不能一一列举。但上面的例子希望能说明我更关注最本质、最核心的问题，如元、次数、立体几何中形的构架等。

（3）高观点下的数学。站在高处去看数学问题，是一种风景独好的感受。对于学有余力的学生，让他们接触更多的数学，学更高处的数学，而不是反复低效地刷题更能培养人。所以，在教材之外，我会教授我的学生更多的数学。如极限（严格定义的极限）、微分中值点等数学分析的部分内容、复数的三角形式及其应用、解析几何中直线所成的角、立体几何空间的距离等。而这种高观点的渗透也使得学生对数学问题看得更深刻，甚至可以站在命题人的角度去审视问题。例如，2017 年浙江数学高考的最后一题：

已知数列｛xn｝满足：x1=1，xn=xn+1+ln（1+xn+1），（n ∈N*）。证明：当n ∈N*时，①0 ＜xn+1＜xn；②；③

如果学生能够掌握好函数拟合思想及数列的不动点求通项的方法，那么上述问题就可以理解得更深刻。命题人对问题的设计就是带着我们一步一步地研究这个数列。首先是研究数列的单调性，同时，也给出了数列的下界；而由单调有界数列必有极限可知道该数列极限为0。其次是研究数列的增长速率问题，题目中给的递推公式是无法求通项的，所以我们要通过对函数f（x）=x+1n（x+1）进行放缩来估计函数的增长速率，放缩的方式是上限用切线进行拟合，而下限用一次分式拟合，于是就有，上限说明了数列｛xn｝大于一个等比数列，下限则给出了数列大于一个等比数列，这里要用到不动点求数列通项的方法。最后，化简得出｛xn｝增长速率的估值：