机制设计概述，机制设计理论

一、机制设计概述

机制设计是一种把博弈结构设计与博弈过程分析作为一个整体所引出的问题。前面讨论的博弈，把博弈规则当成是外生给定的。在这种情况下的参与人，没有不参加博弈的权利。而现实的许多互动，有的参与人既是博弈规则的设计者，又是博弈规则给定后的参与人。比如在市场竞争中，一家企业想挑起价格战，首先你得能把许多竞争对手引入价格战中，其次才是在价格战中的行动。领头企业一方面在制订行业规则，一方面又在它制定的博弈规则下制订博弈战略，这种局面是必然的，如垄断厂商选择了合同并由合同规定与下游零售商的博弈规则，又在相应规则下博弈。

委托—代理理论本质上就是机制设计的问题。委托人是机制设计者，代理人是在给定机制下愿意参加博弈的人。如拍卖中，要出卖物品的人可以设计拍卖规则。而愿意购买的人，可参与博弈。现在的许多讨论都集中在作为委托人的地位是外生的假设下展开，但在许多情况下，规则设计者的地位也是在互动中产生的，这种情况的讨论不多。

本节主要介绍委托人地位是外生情况下的机制设计的一般原理。

在一个互动过程中，存在一个有外生权利的博弈规则设计者，称为委托人，有一个或多个在委托人设计的规则下进行博弈的参与人，称为代理人。委托人希望选择一个机制，能够最大化自己的效用，但这不是没有条件的，必须要有人愿意加入到这个博弈中，来充当代理人才行。一个自然的要求就是：代理人在博弈中的期望效用要大于不作为代理人而在博弈之外的收益，这一条件称为参与约束或个人理性约束。在有代理人的情况下，委托人由于有自己的效用，希望代理人选择委托人希望的行动。然而代理人只有在符合自己的效用优化原则的情况下，才会偏爱某种行动。这就要求，委托人希望代理人选择的行动，能够使代理人在实施这一行动时达到效用最大化的结果。这一条件称为激励相容约束。实际上，委托人可理解为政策的设计者，代理人可理解为在政策制约下的行为人。委托人希望政策的实施达到某种效果，希望代理人选择某种有利于自己的行为。

理想的委托代理结构应该是委托人希望的行动正是代理人从自身最优考虑后的主动选择。

典型的机制设计是一个三阶段的博弈。

在第一阶段，委托人设计一个博弈机制，如拍卖时，物品出卖者选择拍卖方式，又如招标时规定投标评标方式。这个规则要包括代理人发出什么信号。如拍卖时的报价，招标时的标书的内容。对所发的信号的处理方式，如拍卖中谁获得物品，出什么价，投标时谁中标的决策规则。

第二阶段，潜在的代理人分析规则，到底是否要成为代理人，如拍卖中考虑是否参加拍卖。

第三阶段，接受机制的代理人根据委托人设定的规则进行博弈。

为了对机制设计进行结构化的描述，我们以拍卖机制设计为例来进行讨论。假设一个人有一张古画要出卖，有两个潜在的购买者。商品必须按整体出售。购买者1对该画的价值判断是θ1；购买者2的价值判断是θ2，θ1，θ2是私人信息，可以作为参与人的类型。如果用贝叶斯静态博弈来建模，则要求附加条件：θ1，θ2是随机变量，并且θ1，θ2的分布是公共知识。

卖者可选择进行拍卖的方式，如前面的一级密封拍卖，或在众多的拍卖方式中选择一种，当然也可以设计一种新的拍卖方式。对卖者而言，拍卖方式只是实现自己目标的手段，所以要求有卖者的效用函数。

在一级密封拍卖中，各个参拍人被要求把自己的投标出价同时报出，根据报价决定谁获得拍卖品，支付什么价格。一般地，可以抽象为要求参拍人向拍卖人给出一个信号，根据信号来决定谁将得到物品，这就是配置机制。假设参与人1的信号是s1，参与人2的信号是s2。

信号不一定是报价，可以是其他的，比如要求报出该画的制作时间。根据s1， s2来决定谁将获得该物品的配置规则也可以是按概率的分配规则。比如可规定，参与人1以的概率获得该物品，参与人2以的概率获得该物品的随机配置规则，记x1（s1，s2）为配置给参与人1的概率，x2（s1，s2）为配置给参与人2的概率。在一级密封拍卖中，s1，s2是报价。配置规则是：如果s1＞s2，x1（s1，s2）＝1，x2（s1，s2）＝0，如果s1＜s2，x1（s1，s2）＝0，x2（s1，s2）＝1。总之，配置规则是一个从信号到概率的函数关系。

支付价格是T1（s1，s2），T2（s1，s2）表示参与人1、2按配置规则时要付出的钱，如在一级密封拍卖中，当s1＞s2时，T1（s1，s2）＝s1，T2（s1，s2）＝0，一般说，并不要求没有获得物品的参与人的支付为0。

作为例子，我们可以讨论这样的机制。在古画拍卖中，两个参与人每人支付一万元给卖者，要求同时报出该画距今的年份。s0是该画的真实的年份，拍卖人自己知道。按参与人所报年份与此画的真实年份的误差决定谁获得该画的概率分配，比如，可以用，作为配置规则，这时T1（s1，s2）＝T2（s1，s2）＝1。

在给定的规则下，买者1的参与约束是在采用贝叶斯均衡策略时，期望收益比不参与拍卖要高，若s＊1（θ1），s＊2（θ2）是均衡策略，假如不参与的收益为0，则要求

Eθ2［θ1x1（s＊1（θ1），s＊2（θ2））－T1（s＊1（θ1），s＊2（θ2））］≥0

其中Eθ2（·），是对参与人2的类型取期望。而激励相容约束是他会选择s＊1（θ1）而非其他，因此，要求

Eθ2［θ1x1（s＊1（θ1），s＊2（θ2））－T1（s＊1（θ1），s＊2（θ2））］

≥Eθ2［θ1x1（s1，s＊2（θ2））－T1（s，s＊2（θ2））］

同样地可考虑参与人2的理性约束与激励相容约束。

而卖者，希望最大化

Eθ1Eθ2［T1（s＊1（θ1），s＊2（θ2））＋T2（s＊1（θ1），s＊2（θ2））］

上述表达式在配置规则给定，支付规则给定时是一个定数，但不同的博弈规则下是不同的，最大化卖者的效用就是要回答什么规则可使上式最大。

这一最大化问题将面临着很大的困难。在所有的可用信号中，在每一信号中的所有的配置规则及支付规则中，要回答何者使卖者的收益最大，既有信号空间的选择问题，又有配置支付函数的选择问题，是相当复杂的最优化问题。

直接显示原理帮助我们解决了一部分难题，使信号选择的优化问题可以忽略。

二、机制设计的结构与显示原理

机制设计问题一般可以描述成如下形式：

假定有n＋1个参与人，其中i＝0代表委托人，i＝1，2，…，n代表代理人，委托人没有私人信息，代理人的类型θi是私人信息。θi∈Θi而概率分布p（θ1，θ2，…， θn）是公共知识。委托人的设计任务是规定代理人的信号空间Mi，依据代理人给出的信号m＝（m1，m2，…，mn），决定配置函数xi＝xi（m）及支付函数ti＝ti（m），可以把

y＝（x1（m），x2（m），…，xn（m）；t1（m），…，tn（m））称为机制设计的配置函数。

假定参与人i的效用是ui（y，θ1，…，θn），委托人的效用u0是ti的单调增加函数，ui（i≠0）是ti的严格减函数。

记θ＝（θ1，…，θn）；

x（m）＝（x1（m），x2（m），…，xn（m））；

T（m）＝（t1（m），…，tn（m））。

配置函数y＝（x（m），T（m））＝y（m）是代理人的信号类型依存的，以y（m（θ））表示类型依存的配置。代理人i的期望效用为

Ui（θi）＝Eθ－i｜θi［ui（y（m（θ）），θ－i］

其中（·），表示以p（θ－i｜θi）概率对ui求期望。

委托人的期望效用是：

U0＝Eθu0（y（m（θ）），θ）

上面的描述中指出了信号选择的问题，多种可用的信号中，何者对委托人最有利？这一问题由显示原理给出答案。

显示原理回答了信号的选择对机制设计有什么影响的问题。把Mi＝Θi，i＝1，…，n的信号空间称为直接机制，直接机制是指参与人的类型就是信号，博弈要求代理人所报信号就是直接报出类型，但不一定是报真实的类型。非直接机制称为间接机制，也就是用类型以外的信息作为信号。

显示原理：假设以Mi为信号空间和配置函数y（m（θ））的博弈中其贝叶斯均衡为

m＊＝｛m＊1（θ1），…，m＊n（θn）｝，m＊i∈Mi；θi∈Θi

那么存在一个以Mi＝Θi为信号的直接机制y¯（θ），该机制的贝叶斯均衡是，所有代理人在第二阶段接受机制，在第三阶段报出自己的真实类型θ＝（θ1，…，θn），而均衡配置结果与原来机制的均衡结果相同。

根据显示原理，为了找到一个最优的机制。可以不必在信号上做文章，而采用直接报类型就能达到同样效果。在第三阶段报出真实类型的结论更表明，在这个机制中代理人只要简单地报出自己的真实类型，不必隐瞒什么。也就是说存在着说真话的直接机制是最优机制。

关于不完全信息与资源配置的效率，有下面的定理。(www.xing528.com)

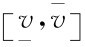卖者的成本是内的随机变量，买者的价值是内的随机变量，假定分布在相应区间上密度为正。如果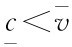，则存在一个正的概率的交易是有效率的（交易成功双方有收益）。则存在一个正的概率的，交易是无效率的（卖者的成本大于购买者的支付）。若有效率的交易与无效率的交易概率都是正的，那么利用所有有效率交易机会且满足参与约束。激励相容约束和预算平衡约束的机制是不存在的。

这一定理表明了机制设计的效率必然有损失。

例4.5.1 双方报价拍卖

若参与人1有一物品要卖，参与人2希望买到该物品。我们规定按以下的规则进行交易，两人分别把希望的成交价格写入信封，如果p1＞p2则交易失败，如果p1≤p2，则以的价格成交，pi为参与人i的报价。

v1是参与人1（卖方）对物品的估价，v2是买方的估价。这些当然是私人信息。但假设v1与v2独立，服从［0，1］上的均匀分布，而且是公共知识。

如果成交，参与人1的效用为p－v1，否则为0，参与人2的效用为v2－p，否则为0，在这种机制下，参与人是否会报出真实的信息，即真实地报出自己的估价。

设（p＊1（v1），p＊2（v2））是贝叶斯纳什均衡，则参与人1选择p＊1（v1）应使

即p＊1（v1）是下面最优问题的解。

同理可得，p＊2（v2）应满足

一般地求解p＊1（v1），p＊2（v2）是困难的，因为在所有类型的函数中求最优难度较大。通常，人们会在某些函数类中求最优，比如在线性函数类中求最优，即在所有的线性函数中，求出能满足最优条件的函数。

设p1（v1）＝a1＋b1v1；p2（v2）＝a2＋b2v2，要求求出a＊1，b＊1；a＊2，b＊2，使

p＊1（v1）＝a＊1＋b＊1v1；p＊2（v2）＝a＊2＋b＊2v2

满足最优条件，最优化条件在线性函数类中的条件是：

分别对上述二式求最优的一阶条件可得

由此，可以看到，一般情况下，参与人不会报出真实的类型。能够成功交易的要求是a＊2＋b＊2v2≥a＊1＋b＊1v1，即。而一般地说v2≥v1时，交易应该发生。这说明，这种规则使交易成功的范围缩小了。

例4.5.2 说实话的直接机制

设有两个投标人，竞投一件物品。v1，v2分别是两人的估价，v1，v2是［0，1］上独立的均匀分布且为共同知识，博弈规则如下：

1.两投标人被要求同时声明v′1，v′2。

2.物品按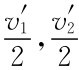的概率在参与人1与参与人2之间分配。

3.每人的支付是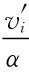，α是常数。

我们希望选择适当的α，能使v′i＝vi，也就是在适当的支付规则下，每人都愿意说真话。

若v′i＝fi（vi）是α给定时的声明策略。v1类型的参与人在报f1（v1）时，收益为

由于

所以时，比任何其它的函数收益高，当α＝2时，f＊1（v1）＝v1，同理f＊2（v2）＝v2。

所以，在规定的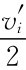的概率获得物品，支付为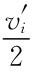时，参与人直接报出真实的类型是最优的。但这一制度由于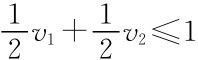，因此，可能发生物品无法卖出的情况。如果改用以与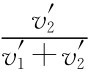的概率来分配物品，物品必可卖出，但分析并求出让买者说真话的支付比较困难。

第4章 习题

1.企业1的成本α是私人信息，他的成本是［1，3］内的均匀分布是公共知识。企业2的成本是2。若是企业1，2的产量，利润为

π1＝q1（10－q1－q2－α）

π2＝q2（10－q1－q2－2）

求贝叶斯均衡。

2.参与人1、2的类型θ1，θ2是私人信息，θ1，θ2独立且服从［－1，1］的均匀分布是公共知识，两个参与人都有A，B两种策略，收益如表：

求纯策略的贝叶斯均衡。

3.一个班级内有2／3的同学是20岁，1／3是19岁，在班中随机抽取一人作为参与人1，另有一人参与人2，要求参与人2猜参与人1的年龄，参与人1判断参与人2能否猜对，收益如表：

求贝叶斯均衡。

4.参与人1、2对某物品的价值判断分别是v1，v2是私人信息，v1，v2独立且服从［0，1］内的均匀分布是公共知识，要求二人同时报价，物品由出高价者获得，支付为另一人的出价的k倍。求使参与人说真话的k。

第4章 参考答案与提示

1.若（qα1）＊，q＊2是贝叶斯均衡，则可导出

解得

2.存在θ＊1，当θ1＞θ＊1时，参与人1选A最优，θ1＜θ＊1时选B最优，存在θ＊2，当θ1＞θ＊2时，参与人2选B最优，θ1＜θ＊1时选A最优。针对参与人2的最优策略，参与人1选A的收益与选B的收益分别是及1－θ1

在θ＊1时，

考虑到θ＊1与θ＊2后参与人的地位的对称性，因此成立θ＊1＝θ＊2，可得θ＊2＝θ＊1＝0

即θ1＞0时参与人选A，θ1＜0时参与人选B，参与人2类似。

在参与人2看参与人1时，有一半人会选A，一半人会选B。

3.参与人2猜20时最少收益是，参与人2猜19时最大收益是1，可以验证参与人猜20时是最优的。

因此，20岁的人判断会猜对，19岁的人判断会猜错，参与人猜20岁时是贝叶斯均衡。

4.k＝1，参看相关例题。