曲线与曲面的拟合方法

岩石地基与边坡中会遇到曲面或曲线（地形面、结构面）拟合及求交问题，本节介绍一些有关的知识和算法。

一、曲线的三次参数样条拟合

常见的曲线拟合是将已知的特征点依次排列，分段用多项式插值。这种方法较简单，但需要较多的条件。例如，在已知曲线段首尾两点坐标和切矢的条件下，可用三次多项式拟合Ferguson曲线段，即

式中：r（1）、r（2）分别为起点和终点坐标；t（1）、t（2）分别为起点和终点切矢；[C]为常数矩阵，根据曲线的C1连续要求，常数矩阵[C]为

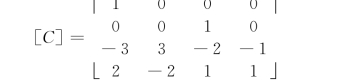
显然，在实际工程中提供满足上述要求的测量数据是困难的，为此可以采用三次参数样条曲线来处理曲线拟合问题。三次参数样条曲线是次数最低的二阶光滑连续样条曲线，具有计算量少和稳定性好的特点（Prenter，1975）。

在空间给定n+1个顶点Pi（i=0，1，2，…，n），并给定参数分割Δt：t 0＜t 1＜…＜tn-1＜tn，三次参数样条曲线P（t）满足下列条件：

（1）在每个小区间[ti-1，ti]（i=1，2，…，n）上，P（t）是三次参数多项式。

（2）在整个区间[t 0，tn]上，P（t）具有二阶参数连续性，即在结点ti（i=1，2，…，n-1）处，有

（2）建立m连续方程组。采用Hermite插值公式，在区间[ti-1，ti]上，有三次参数样条曲线

式（1-2-6）称为三次参数样条曲线P（t）的m连续方程组。

（3）构造边界条件m 0和mn。在式（1-2-6）中有n+1个未知量，但只有n-1个方程组，因此需要构造两个边界条件m 0和mn，便可唯一地求出全部未知量。

借助三次Bezier曲线

通过计算可得

[A]是严格三对角占优矩阵。

二、曲面的参数拟合

地形面和大规模结构面是不规则曲面。计算机辅助几何设计（CAGD）中一些常用的曲面构造方法，如孔斯曲面（Coons Surface），对大尺度且几何信息不充分的曲面往往不适用，因为这些方法往往要求许多面片的角点坐标{X}、切矢{Xs}、{X t}和扭矢{X st}等数据，这些要求在实际工程中很难得到满足。若采用一些近似方法，又可能导致曲面严重变形。

笔者认为以下两种方法可以解决计算岩体力学中的不规则曲面拟合问题。

1.工程地质插值公式

工程地质领域广泛采用以下插值公式来描述地形面。若给出地形面上n个点的坐标为

令R：[a，b]*[c，d]为u—v平面内一矩形域，定义于该矩形域的连续曲面记为

式（1-2-20）中，对曲面Z运用的算符L和M为一线性操作。

有别于常见的曲面片拼接型的曲面构造，混和样条插值曲面对原曲面进行的是一种整体拟合，适用于大尺度曲面的拟合问题。若令p=2，则该曲面保有C2的连续性，这是不规则曲面三角离散所必须的。又因曲面边界的切矢条件在岩体工程中并无特别意义，故可将其忽略，即

式（1-2-22）中样条基函数可以作为固定模块直接编入程序，根据不同的n或n′直接调用。如果已知曲线网格式（1-2-17）上的一些点，利用三次样条插值曲线便可拟合出n+n′条曲线参数方程f j（u）、g i（v），然后利用式（1-2-22）便可得到曲面（1-2-16）。将曲面参数方程（1-2-15）看作定义于同一矩形域的3个独立的曲面方程，依次用上述方法拟合，从而得到不规则曲面的参数表示。

上述简化处理会使曲面临近边界的区域发生一些变形，但与机械、数控操作等领域所研究的精密几何形体不同，这些误差在岩体工程中是可以接受的。如果选择一个恰当的辅助面，这种影响还会得到更好的控制。(www.xing528.com)

三、曲面（参数曲面与隐式曲面）求交

曲面求交是定义复杂三维实体轮廓面的重要步骤，是CAD/CAM系统的核心算法，有些问题至今仍未得到解决。笔者采用了一种参数曲面与隐式曲面求交的算法来解决这一问题。从理论上讲，各种类型的曲面求交都可以归结为参数曲面与隐式曲面求交的形式（石教英，蔡文立，1996；余正生，彭群生，马利庄，1999）。

设某一参数曲面为

其定义域为Ωg。

设另一隐式曲面为

其定义域为Ωf。

对由式（1-2-23）和式（1-2-24）定义的两曲面求交，实际上就是求解方程

由于式（1-2-25）结构复杂，次数较高，因此通常采用数值解法。例如，可以利用二维标量场抽取等值线原理求解式（1-2-25）。令Ω=Ωf∩Ωg，h（u，v）=0的解视为二维标量场Ω内的等值线h（u，v）=0，抽取等值线的过程为：

图1-2-1　正则化网格

（1）建立正则化网格（图1-2-1），在u和v方向作n u和n v等分，记

则有

每一个正则化网格单元Δij的4个顶点分别为（u i，v j）、（u i，v j+1）、（u i+1，v j）、（ui+1，v j+1），i=0、1、2、…、nu-1，j=0、1、2、…、n v-1。对应的函数值为hi，j、hi，j+1、hi+1，j、hi+1，j+1。

（2）将网格排列次序，在每个单元内寻找相应的等值线段，即在定义域Ω内满足h（u，v）=0的线段，处理完所有单元后，即自然生成定义域Ω内的等值线分布。

为在Δij内生成等值线，首先需要计算等值线与网格单元的交点，然后连接交点，形成单元内的等值线。

等值线与网格单元交点的计算，关键是计算单元的各边与等值线的交点，假设函数h（u，v）在单元内呈线性变化，可以通过顶点判断和边上插值的方法计算交点，具体步骤如下：

（1）若hi，j≤0，则顶点（ui，v j）记为“-”，否则记为“+”。

（2）若单元4个顶点全为“+”，或全为“-”，则单元与等值线无交点，返回步骤（1），否则转向步骤（3）。

（3）对于两个顶点分别为“+”、“-”的单元边，可用线性插值计算等值线与该边的交点。在图1-2-2中，设（ui，v j）为“-”、（ui，v j+1）为“+”，则交点为

图1-2-2　等值线与网格单元的交点

该单元其他边上的交点可以用相同方法求得。若网格单元Δij的“+”、“-”顶点交叉分布，则交点的连接可能有两种形式（图1-2-3）。为了克服这种二义性的连接，可采用St.Andrew的单元（图1-2-4）。其基本思想是：利用对角线将Δij分成4个三角形，求出中心点（u mid，v mid）的函数值hmid=h（u mid，v mid），等值线的抽取直接在每个三角形单元进行，每个三角形单元至多只包含一条等值线段（图1-2-5）。

图1-2-3　等值线二义性的连接

图1-2-4　St.Andrew的单元划分

图1-2-5　单元内抽取等值线的几种可能情况