多项式拟合达到多阶曲线拟合

多阶曲线法是根据研究对象的历史数据，用多项式曲线模型去描述研究对象随时间变化的发展规律，并根据该模型预测事物未来发展状况的一种时间序列分析方法。多阶曲线预测模型的一般形式为

其中：yt为时间序列观测值；yˆt为时间序列的估计值；t为自变量时间（可设t =t1 ,t2,…,tn，一般令t1=1,ti+1=ti+1）；εt为随机波动引起的误差（通常假定εt为独立同分布、期望是0的正态序列）；ai为拟合系数(i=0,1,…,k)。

多项式函数的图形有个特点，即其曲线“拐的弯数”比多项式的次数少1。图7.2.1给出了直线、二次曲线与三次曲线的大致图像，从图中可以明显看出这个特点。

图7.2.1　多项式函数的图形

绘制出时间序列图后，先观察图形是否有显著的趋势，若有，再观察图形的拐弯情况，根据图形拐弯的走势大致判断可用几次多项式模型。不过，有时不好明确实际序列图拐的弯数，如图7.2.2所示，通过散点图不好确定，就画出序列折线图（打开SPSS后，选择“分析”→“时间序列预测”→“序列图”即可）。由图7.2.2可见，可以看成拐了一个大弯，还可以看作拐了两个弯，或者三个弯等。这种情况，通常选择至少两种多项式模型来拟合，选择拟合程度较好的作为分析和预测模型。

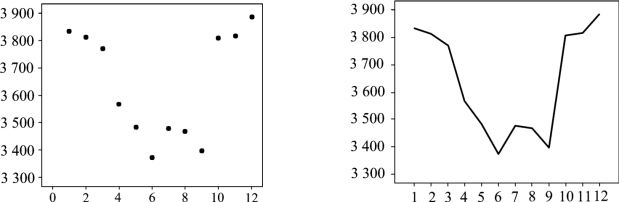
图7.2.2　序列图

那么，是不是多项式模型的次数越高，对数据的拟合程度越好呢？

答案是否定的，随着多项式函数次数的增加，曲线会越来越多地把尽可能多的点拟合进去。但在现实世界中，我们拿到的样本点通常是带有误差的，这些样本点并不一定完全符合某个函数的关系，若我们无限制地增加函数的次数去拟合样本点，就会造成即使某些样本点有错误有偏差也会把它拟合进去，这样会使函数变得极其复杂，对于新的样本点的预测结果将会产生极大的偏差，这就是过拟合。那么如果样本点本来是符合高次函数，却使用较低次的多项式函数去拟合它，如图7.2.3所示，大多数样本点将不能拟合到左图的直线上，这时再用这个直线函数去预测新来的样本点时，预测结果也将产生很大的偏差，这就是欠拟合。总之，多项式的次数越高，越会产生振荡现象，会影响精度，从而会造成过拟合，当然，我们也不能欠拟合，图7.2.3给出了欠拟合、正好与过拟合三种情况。

图7.2.3　欠拟合、正好与过拟合

实际中，常用的是一次曲线、二次曲线和三次曲线模型，有时也用到四次曲线模型，五次与六次等更高次的模型用得较少。理论上，时间序列中时间的取法及多项式模型中的拟合系数，可以通过以下方式来获得。

1. 时间序列时间的取法

在计算拟合系数时，常常遇到∑ti或者t，为方便计算，要对时间项进行处理。当时间点t1 ,t2,…,tn 为连续等间隔时，取时间序列的中间为原点。

数据项数为奇数（n=2m+1）时，该时间序列取为

数据项数为偶数（n=2m）时，该时间序列取为

2. 多项式模型及拟合系数

直线、二次曲线、三次曲线的图像如图7.2.1所示。处理数据时，常根据趋势图来选择曲线类型。

① 直线模型：y=a+bt。

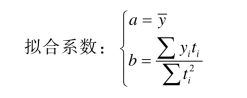
模型分析：处理实际问题时，要注意分析“斜率和截距的实际意义”。

模型分析：处理实际问题时，可以对二次曲线进行“单调性及极值分析”。

模型分析：处理实际问题时，可以对三次曲线进行“单调性及拐点分析”。

实际操作中，一般通过计算机软件（SPSS、SAS、Excel等）来完成拟合系数的计算，且在时间序列的自变量时间的取法上可直接采取真实的时间值或者令t1=1，ti+1=ti+1，后者更常用。那么，究竟哪种模型更合适，我们通常可以借助软件多尝试几种，选择拟合程度较高的即可。下面我们结合软件SPSS来完成例1。

例1 表7.2.1中的数据给出了1986—2010年全国出入境边防检查机关每年共查验出入境人员的人次数，请研究数据变化的规律，并预测未来三年的情况。(www.xing528.com)

表7.2.1　全国出入境人员统计数据

注：该数据来自国家移民管理局的官方网站https://www.nia.gov.cn/n741440/n741567/index.html。

解 （1）先用SPSS绘制时间序列图（图略），根据其趋势可以用多项式模型来拟合。

（2）分别选用一次、二次与三次多项式进行拟合。

由于多项式模型属于能转化成线性问题的非线性拟合模型，即可运用最小二乘法求得其模型参数，这个过程实际上是回归分析中求参数的方法，故运用SPSS求得模型参数的步骤与回归分析的操作步骤一样。打开SPSS后：

① 选择“分析”→“回归”→“曲线估算”命令，会出现图7.2.4的对话框。

② 导入因变量，点击“时间”，这样默认的（自变量）时间是1, 2, …, 25（给了25年的数据），勾选“线性”，注意“模型绘图、显示ANOVA表”等处勾选。

③ 点击图7.2.4右上角的“保存”，会出现图7.2.5的对话框。

图7.2.4　“曲线估算”命令

图7.2.5　“曲线估算：保存”命令

④ 勾选图7.2.5中的预测值，并点击预测范围，填上观测值28（这样不仅给出了原来25个数据的预测值，也给出了2011—2013年的预测值），点击“继续”，关闭该对话框，回到图7.2.4的对话框，点击确定即可得到图7.2.6中的第一张图，并可知R2 =0.943，表达式为

用上述同样的步骤分别在对话框“曲线估计”的模型中勾选“二次”与“三次”，就可得到图7.2.6中的第二张图与第三张图，并且“二次”对应的2 0.988 R=，表达式为

“三次”对应的R2 =0.991，表达式为

（3）确定预测模型及未来三年的预测值。

从上面的判决系数可以看出三次模型拟合得最好，这点从图7.2.6也可以看出。

图7.2.6　曲线拟合图

它们对未来三年的预测值见表7.2.2。从表7.2.2中可见，三次模型的预测值与2011—2013年的实际值最贴切。

表7.2.2　预测值与实际值

另外，在实际操作时，线性、二次与三次可同时由SPSS呈现出来，只需在进行到图7.2.4的步骤时，将对话框中的模型中的“线性、二次与三次”同时勾选，其他操作一样，这时会把图7.2.6中的三条线叠加在一张序列图中，并得到表7.2.3。

表7.2.3　模型摘要和参数估算值